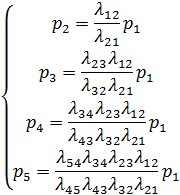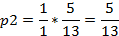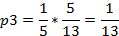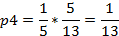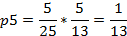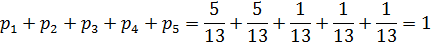Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пр.13 «Составление систем уравнений Колмогорова. Нахождение финальных вероятностей»Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
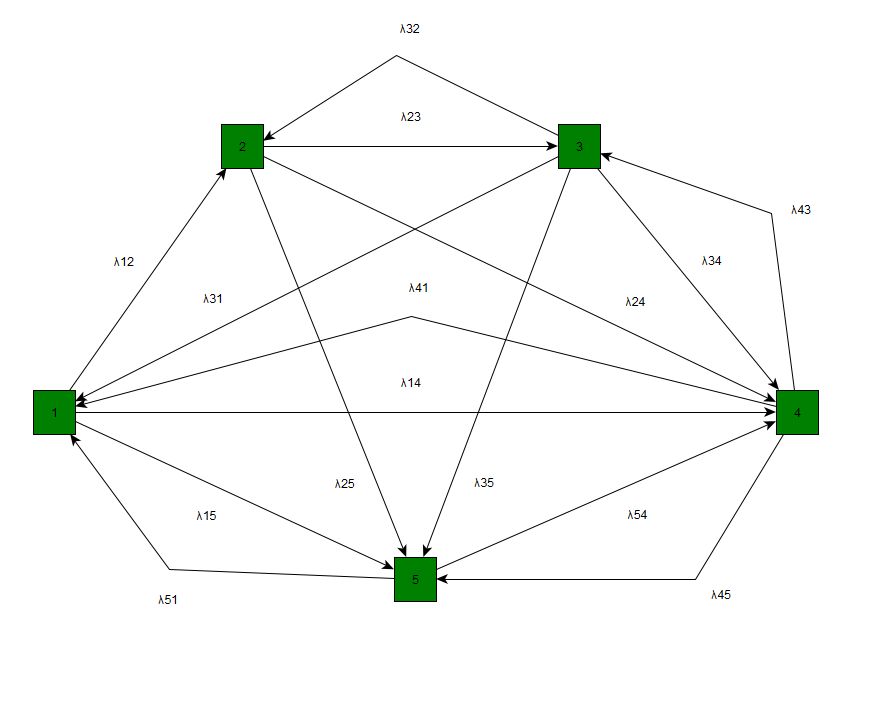
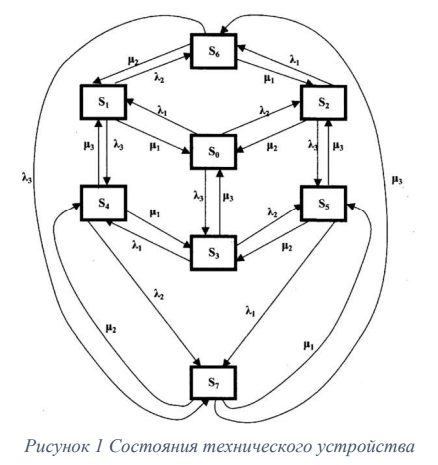
Цель: 1. Отработать и закрепить умения составлять системы уравнений Колмогорова для непрерывной цепи Маркова. 2. Отработать и закрепить умения находить финальные вероятности состояний непрерывной цепи Маркова. Задача 1. Составить систему дифференциальных уравнений Колмогорова, для непрерывной Марковской цепи, характеризующейся графом состояний из первого задания Практической работы №12. Вариант №6 Начертим размеченный граф состояний, соответствующий матрице P.
Рис.1
Рис.2 Размеченным графом будем считать такой граф, у которого стрелками указаны переходы из одного состояния в другое, а рядом со стрелкой указана интенсивность перехода. Будем различать 2 интенсивности – прямую λ, и обратную u. Тогда На основе построенного размеченного графа создадим математическую модель. Наше техническое устройство в соответствии с построенным графом в любой момент времени будет находиться в одном из восьми возможных состояний. Обозначим вероятность каждого i-го состояния как pi(t), тогда
Для определения вероятности каждого состояния технического устройства составим соответствующие дифференциальные уравнения:
Задача №2 Техническое устройство состоит из 3узлов и в любой момент времени может находиться в одном из состояний.
Численные значения интенсивности потоков событий: Найти финальные вероятности состояний устройства с помощью таблиц MS Excel.
Решение:
Подставим Значения из таблицы и упростим уравнения.
Для составления матриц этой системы уравнений и автоматизации процесса решения, запишем ее в следующем виде:
Таким образом в этой системе имеем матрицу А:
Матрица свободных членов В:
Матрица неизвестных Х:
Чтобы найти решение – вектор столбец Х, в MS Excel нужно с помощью соответствующих функции «МОБР» найти матрицу обратную к матрице А и умножить ее на вектор-столбец В.
Получив решение необходимо выполнить проверку нормировочного условие, т.е. сумма найденных неизвестных членов должна быть равна 1.
Пр.14 «Вычисление предельных вероятностей состояний для процесса гибели и размножения» Цель: Отработать и закрепить умения вычислить предельные вероятности состояний для процесса гибели и размножения. Вариант 26. Дана система, которая может находиться в одном из пяти состояний. Система работает по схеме процесса гибели и размножения, граф которого показан на рисунке Рис. 1
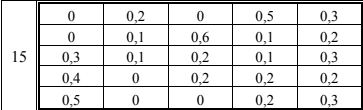
Рис.1 Числовые значения интенсивности перехода системы из состояния в состояние заданы в таблице 1.
(Табл. 1)
Решение: Вычислим финальные вероятности событий. Составим систему линейных уравнений: для первого состояния S1 имеем:
для второго состояния S2 суммы членов, соответствующих входящим и выходящим стрелкам, равны:
Но, в силу (1.1), можно сократить справа и слева равные друг другу члены
Так же для события S3:
для события S4:
и для события S5:
Итак, предельные вероятности
Решим эту систему уравнений. Будем решать эту систему следующим образом: из первого уравнения выразим p2:
из второго, с учетом (1.2), получим:
из третьего, с учетом (1.3), получим:
из четвертого, с учетом предыдущего, получим:
Подставим вероятности в нормировочное условие:
Получаем
Вставим числовые значения в формулу:
Остальные вероятности выражаются через
Подставим числовые значения:
Проверим правильность вычислений, подставив найденные значения предельных вероятностей в нормировочное условие:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 1081; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.155.253 (0.009 с.) |

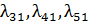 - интенсивности потоков отказов соответственно первого узла, а
- интенсивности потоков отказов соответственно первого узла, а 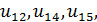 - соответственно интенсивности потоков возвратов узлов.
- соответственно интенсивности потоков возвратов узлов.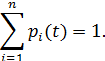
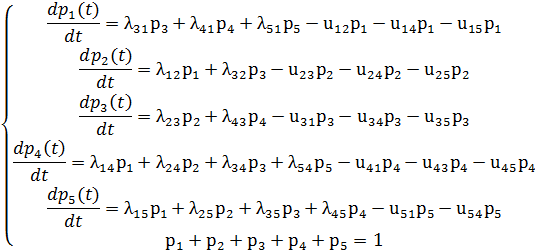
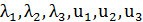 по вариантам даны в таблице.
по вариантам даны в таблице.
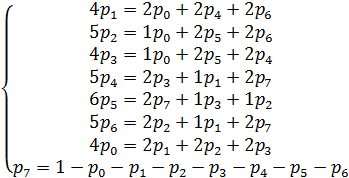
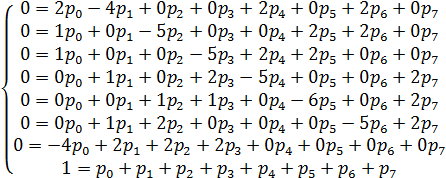

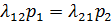 (1.1)
(1.1)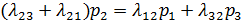
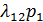 и
и 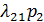 и получим:
и получим: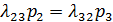
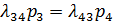
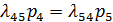
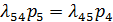
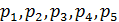 в этой схеме гибели и размножения удовлетворяют уравнениям и нормировочному условию:
в этой схеме гибели и размножения удовлетворяют уравнениям и нормировочному условию: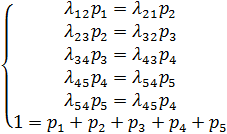
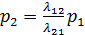 (1.2)
(1.2)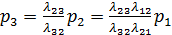 (1.3)
(1.3)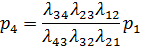
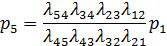
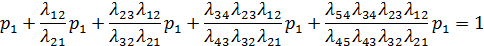
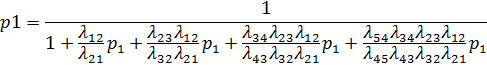
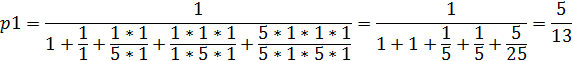
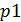 :
: