
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ПО «Математическому моделированию»Содержание книги Поиск на нашем сайте
ВЫПОЛНИЛ: Студент группы ИСП-О-18 Кукушкин А.А.
ПРОВЕРИЛА: Шелепова Т.С.
Оценка ___________________
п. Электроизолятор 2020 г. Цели: 1. Отработать и закрепить умения записывать условие задачи в виде математических формул. 2. Отработать и закрепить умения записывать взаимосвязь показателей задачи в виде простейшей математической модели.
Прежде чем построить математическую модель задачи, т.е. записать ее с помощью математических символов, необходимо четко разобраться с экономической ситуацией, описанной в условии. Для этого необходимо с точки зрения экономики, а не математики, ответить на следующие вопросы: 1) Что является искомыми величинами задачи? 2) Какова цель решения? Какой параметр задачи служит критерием эффективности (оптимальности) решения, например, прибыль, себестоимость, время и т.д. В каком направлении должно изменяться значение этого параметра (к max или к min) для достижения наилучших результатов? 3) Какие условия в отношении искомых величин и ресурсы задачи должны быть выполнены? Эти условия устанавливают, как должны соотноситься друг с другом различные параметры задачи, например, количество ресурса, затраченного при производстве, и его запас на складе; количество выпускаемой продукции и емкость склада, где она будет храниться; количество выпускаемой продукции и рыночный спрос на эту продукцию и т.д. Только после экономического ответа на все эти вопросы можно приступать к записи этих ответов в математическом виде, т.е. к записи математической модели. 1) Искомые величины являются переменными задачи, которые, как правило, обозначаются малыми латинскими буквами с индексами, например, однотипные переменные удобно представлять в виде X = (x1, x2, …, xn). 2) Цель решения записывается в виде целевой функции, обозначаемой, например L(X). Математическая формула ЦФ L(X) отражает способ расчета значений параметра – критерия эффективности задачи. 3) Условия, налагаемые на переменные и ресурсы задачи, записываются в виде системы равенств или неравенств, т.е. ограничений. Левые значения ограничений отображают способ получения (расчет или численные значения из условия задачи) значений тех параметров задачи, на которые были наложены соответствующие условия. В процессе записи математической модели необходимо указывать единицы измерения переменных задачи, целевой функции и всех ограничений. Построим модель задачи №21, используя описанную методику. Переменные задачи: В задаче №21 требуется установить, сколько нужно произвести автомашин марок А1 и А2. Поэтому искомыми величинами, а значит, и переменными задачи являются количество произведённых автомашин каждого вида:
Целевая функция: В условии задачи №21 сформулирована цель – определить план выпуска, обеспечивающий предприятию максимальную выручку. Т.е. критерием эффективности служит параметр кол-ва запасов сырья, который должен стремиться к максимуму. Потому запишем ЦФ в виде суммы всех видов предметов.
Ограничения: Возможные покупки ограничиваются следующими условиями: · Комплекты заготовок металлоконструкций 17шт. не более 17; · Комплект резиновых изделий 11шт. не более 11; · Двигатели с арматурой и электрооборудованием 6 комплектов не более 6; · Двигатели с арматурой и электрооборудованием 5 комплектов не более 5.; · На покупки выделяется не менее 12 тыс. д.е.; · Кол-во купленных предметов не может быть отрицательным. Таким образом, все ограничения задачи №21 делятся на 3 группы, обусловленные: 1) Расходом выделенных денежных средств; 2) Спросом на все товары. 3) Не отрицательностью купленных предметов. Ограничения по покупке любого из предметов имеют следующую содержательную форму записи
Запишем эти ограничения в математической форме. Левая часть ограничения – это количество сделанных автомашин. Правая часть ограничения – это количество автомашин, которое требуется сделать. Таким образом, ограничение вид: S1
S2
S3
S4
Примечание 1.1 Следует всегда проверять размерность левой и правой части из ограничений, поскольку их несовпадение свидетельствует о принципиальной ошибку при составлении ограничений. Не отрицательность предметов задается как
Таким образом, математическая модель этой задачи имеет вид
Цель: Отработать и закрепить умения записывать условие произвольной задачи линейного программирования в виде ОЗЛП. Вариант 2 1
Решение: Введем дополнительные переменные y 1, y 2, y 3, y 4. Причем в третье неравенство введем неотрицательную переменную y 3 со знаком плюс, а в первое, второе и четвертое – со знаком минус переменные y 1, y 2, y 4 запишем задачу в виде:
Перейдем от задачи нахождения максимума целевой функции к задаче нахождения минимума, помножив целевую функцию на (-1)
Таким образом, мы перешли от произвольной ЗЛП к эквивалентной ей ОЗЛП. По правилу приведения ЗЛП к ОЗЛП, если в исходной задаче некоторое ограничение было неравенством, то оно преобразуется в равенство, введением в левую часть некоторой неотрицательной переменной.
Цель: Отработать и закрепить умения графически решать системы неравенств, с двумя переменными. Вариант 11.
Решение: Для построения математической модели остается только идентифицировать переменные и представить цель и ограничения в виде математических функций этих переменных.
Таким образом, мы приходим к следующей математической задаче: среди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значение F max. Построим многоугольник решений. Для этого в системе координат X1 X2 на плоскости изобразим ограниченные прямые:
Взяв какую-либо точку, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство. Полуплоскости, определяемые неравенствами, на рисунке показаны стрелками. Области решений нет, функция не ограничена сверху.
Цель: Отработать и закрепить умения решения ЗЛП симплекс-методом. Вариант 9. Найти максимум функции
Если система ограничений имеет вид:
Решение:
Для составления симплекс-таблиц систему ограничений и функцию F необходимо представлять и в следующем виде:
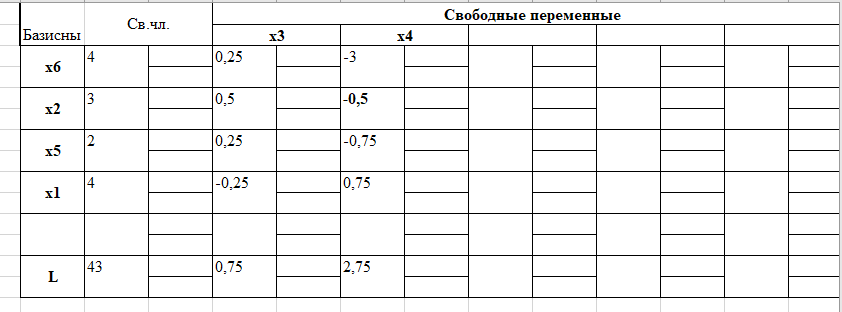
Первый шаг симплекс-метода, составляем таблицут1.1
Таблица 1.1
Ответ: Х = (4,3,0,0,2,4) L = 43 Цель: 1. Отработать и закрепить умения записывать условие транспортной задачи в виде математических формул. 2. Отработать и закрепить умения записывать взаимосвязь показателей транспортной задачи в виде математической модели.
Определение переменных Обозначим количество изделий, выпускаемых из i-го филиала в j-ый пункт потребления через
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 98; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.104.175 (0.007 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Решение:
Решение: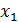 – количество произведённых автомашин А1. (шт.)
– количество произведённых автомашин А1. (шт.)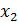 – количество произведённых автомашин А2. (шт.)
– количество произведённых автомашин А2. (шт.)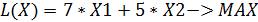
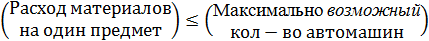
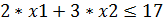
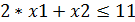 ;
;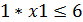 ;
;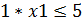 ;
;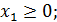
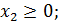
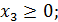

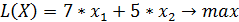
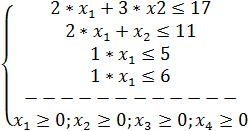
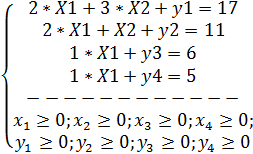
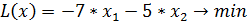
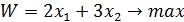
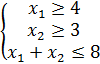
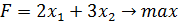
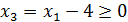
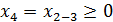
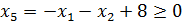

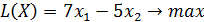 ,
,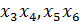 - свободные переменные
- свободные переменные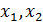 - базисные переменные (зависят от свободных)
- базисные переменные (зависят от свободных)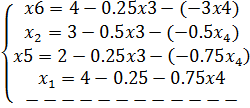
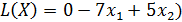
 Решение:
Решение: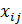 .
.


