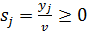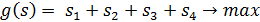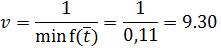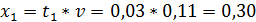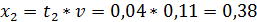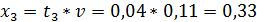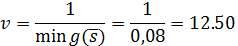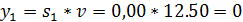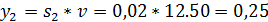Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пр.15 «Расчет характеристик многоканальной СМО»Содержание книги Поиск на нашем сайте
Цель работы: Отработать и закрепить умения находить численные значения характеристик многоканальной системы массово обслуживания с очередью. Вариант 15. На вход системы, имеющей 9 терминалов обслуживания заявок, поступают заявки с интенсивностью λ = 2. Среднее время обслуживания заявки равно T = 3. Если терминалы заняты, то заявка встает в очередь. Дана таблица с номерами характеристик многоканальной СМО
Решение: Коэффициент загрузки:
Вероятность того, что в системе не будет заявок
Вероятность наличия очереди:
Средняя длина очереди:
Пр.16 «Расчет характеристик СМО» Цель работы: Отработать и закрепить умения находить численные значения характеристик системы массово обслуживания, в зависимости от вида системы. Вариант 5. Оптовый склад лесоматериалов обслуживает 30 предприятий-потребителей. Каждое из предприятий направляет на склад за лесоматериалами автомашину в среднем 0,5 раза в смену (продолжительность смены 8 ч). На складе имеются два крана, которые используются только для погрузки лесоматериалов на прибывающие автомашины. Средняя продолжительность погрузки одной автомашины составляет 30 мин. Прибывшая на склад автомашина становится в очередь, если оба крана заняты погрузкой других автомашин. Определите: 1) вероятность того, что оба крана свободны (простаивают); 2) среднее число свободных (незанятых) кранов; 3) коэффициент простоя крана; 4) среднее число автомашин, находящихся на складе (под погрузкой и в ожидании погрузки); 5) среднее число автомашин, находящихся в очереди (длину очереди); 6) коэффициент и среднее время простоя автомашин в очереди. Решение: Данная задача представляет из себя многоканальную систему с неограниченной очередью. n = 2 𝜆 = 2, μ = 1.875 Коэффициент загрузки
Пр.18 ««Решение игр в смешанных стратегиях. Сведение игры к задаче линейного программирования» Цель работы: 1. Отработать и закрепить умения составлять для конечной парной антагонистической игры платежные матрицы для игроков по условиям игры. 2. Отработать и закрепить умения определять основные параметры матричной игры: верхнюю и нижнюю цены игры, максиминную и минимаксную стратегии, чистую цену игры. 3. Отработать и закрепить умения сводить игру размера mxn заданную платежной матрицей к двойственным задачам линейного программирования. 4. Отработать и закрепить умение находить решение матричной игры mxn в смешанных стратегиях с помощью надстройки «Поиск решения» MS Excel. Задача 1 Каждый из игроков А и В записывает одно из чисел N1,N2,N3 или N4, затем они одновременно показывают написанное. Если оба числа оказались одинаковой четности, то игрок А выигрывает столько очков, какова сумма этих чисел, если разной четности – выигрывает игрок В. Составить платежную матрицу, найти нижнюю и верхнюю чистые цены игры, максиминную и минимаксную стратегии игроков. Указать наличие седловой точки (если она есть).
Решение 1. Составим платежную матрицу Пусть
Если 1-й участник применит первую стратегию и второй участник тоже (оба запишут 3), то оба числа оказываются одинаковой четности, участник А выигрывает 3 + 3 = 6. Если 1-й участник применит первую стратегию (напишет 3), а второй участник использует вторую стратегию (напишет 4), то оба числа оказываются разной четности, участник В выигрывает 3+ 4 = 7. Если 1-й участник применит первую стратегию (напишет 3), а второй участник использует третью стратегию (напишет 9), то оба числа оказываются одинаковой четности, участник А выигрывает 3 + 9 = 12. Если 1-й участник применит первую стратегию (напишет 3), а второй участник использует четвертую стратегию (напишет 8), то оба числа оказываются разной четности, участник В выигрывает 3 + 8 = 11. Если 1-й участник применит вторую стратегию (напишет 4), а второй участник использует первую стратегию (напишет 3), то оба числа оказываются разной четности, участник В выигрывает 4 + 3 = 7. Если 1-й участник применит вторую стратегию (напишет 4), а второй участник использует вторую стратегию (напишет 4), то оба числа оказываются одинаковой четности, участник А выигрывает 4 + 4 = 8. Если 1-й участник применит вторую стратегию (напишет 4), а второй участник использует третью стратегию (напишет 9), то оба числа оказываются разной четности, участник В выигрывает 4 + 9 = 13. Если 1-й участник применит вторую стратегию (напишет 4), а второй участник использует четвертую стратегию (напишет 8), то оба числа оказываются одинаковой четности, участник А выигрывает 4 + 8 = 12. Если 1-й участник применит третью стратегию (напишет 9), а второй участник использует первую стратегию (напишет 3), то оба числа оказываются одинаковой четности, участник А выигрывает 9 + 3 = 12. Если 1-й участник применит третью стратегию (напишет 9), а второй участник использует вторую стратегию (напишет 4), то оба числа оказываются разной четности, участник В выигрывает 9 + 4 = 13. Если 1-й участник применит третью стратегию (напишет 9), а второй участник использует третью стратегию (напишет 9), то оба числа оказываются одинаковой четности, участник А выигрывает 9 + 9 = 18. Если 1-й участник применит третью стратегию (напишет 9), а второй участник использует четвертую стратегию (напишет 8), то оба числа оказываются разной четности, участник В выигрывает 9 + 8 = 17. Если 1-й участник применит четвертую стратегию (напишет 8), а второй участник использует первую стратегию (напишет 3), то оба числа оказываются разной четности, участник В выигрывает 8 + 3 = 11. Если 1-й участник применит четвертую стратегию (напишет 8), а второй участник использует вторую стратегию (напишет 4), то оба числа оказываются одинаковой четности, участник А выигрывает 8 + 4 = 12. Если 1-й участник применит четвертую стратегию (напишет 8), а второй участник использует третью стратегию (напишет 9), то оба числа оказываются разной четности, участник В выигрывает 8 + 9 = 17. Если 1-й участник применит четвертую стратегию (напишет 8), а второй участник использует четвертую стратегию (напишет 8), то оба числа оказываются одинаковой четности, участник А выигрывает 8 + 8 = 16.
Таким образом, получим матрицу выигрышей участника А:
Величина
Величина
Поскольку Цена игры находится в пределах:
Задача 2 Дана платежная матрица игры. Решить матричную игру с помощью сведения к задаче линейного программирования и надстройки MS Excel "Поиск решения": 1. Свести игру, заданную платежной матрицей к двойственным задачам линейного программирования. 2. С помощью надстройки «Поиск решения» MS Excel решить полученные задачи. 3. Определить оптимальные смешанные стратегии игроков А и В 4. Определить цену игры Вариант №15
1. Сведение матричной игры к задаче линейного программирования Теория игр находится в тесной связи с линейным программированием, так как каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного программирования. Находим нижнюю цену игры:
Находим верхнюю цену игры:
Поскольку Цена игры находится в пределах:
Решением игры являются смешенные стратегии игроков
1.1. Для первого игрока составим задачу линейного программирования. Применение первым игроком оптимальной стратегии должно обеспечивать ему при любых действиях второго игрока выигрыш не меньше цены игры v:
Величина v неизвестна, однако можно считать, что цена игры v > 0. Преобразуем систему ограничений, разделив все члены неравенств на v:
По условию х1 + х2 + х3 +x4 = 1. Разделим обе части этого равенства на v:
Оптимальная стратегия игрока А должна максимизировать величину v, следовательно, функция должна принимать минимальное значение:
Таким образом, имеем задачу линейного программирования. 1.2. Аналогично для второго игрока составим задачу линейного программирования (двойственная задача):
Оптимальная стратегия игрока В должна минимизировать величину v, следовательно, функция:
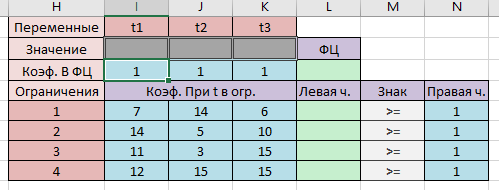
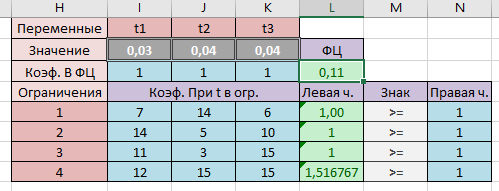
Таким образом, для нахождения решения игры имеем пару двойственных задач линейного программирования. 2. Решение задачи линейного программирования Найдем решение с помощью надстройки Excel Поиск решения. Представим рабочий лист Excel с занесенными исходными данными:
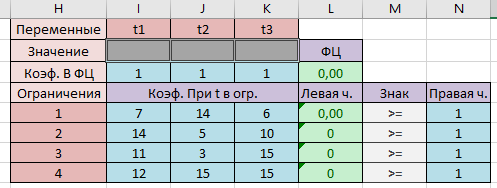
В ячейках I3:K3 будут значения переменных t1, t2, t3. Далее в ячейку L3 заносим значение целевой функции. Для этого используем встроенную математическую функцию СУММПРОИЗВ(). Далее ячейку с функцией L3 копируем в левые части ограничений, т.е. в ячейки L5, L6, L7 и L8.
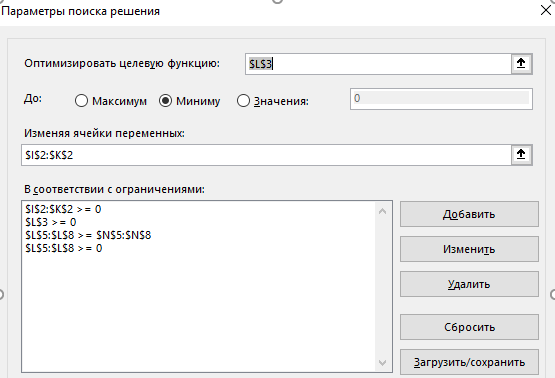
Теперь воспользуемся надстройкой Поиск решения.
Результат решения
Находим значение седловой точки (цена игры):
Находим оптимальные стратегии первого игрока:
Если первый игрок с вероятностью 0,30 будет применять первую стратегию, вторую с вероятностью 0,38 будет вторую и третью 0,33, то при достаточно большом количестве игр с данной матрицей его выигрыш в среднем составит не менее 9,30 2.1 Решение задачи линейного программирования Найдем решение с помощью надстройки Excel Поиск решения. Представим рабочий лист Excel с занесенными исходными данными:
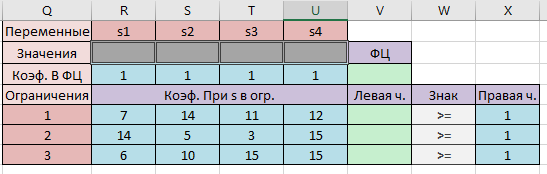
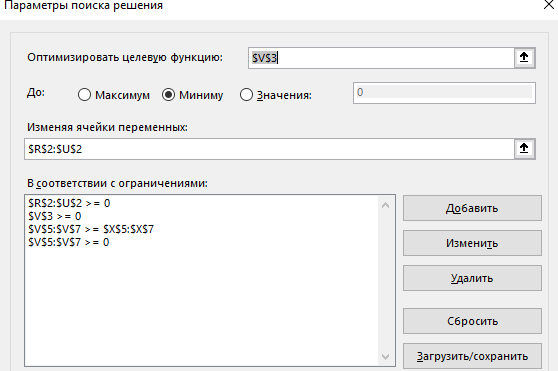
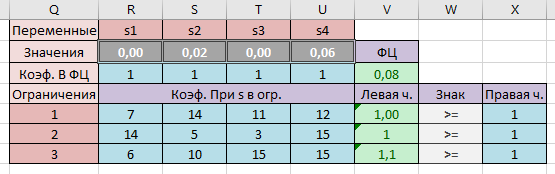
В ячейках R2: U2 будут значения переменных s1, s2, s3, s4. Далее в ячейку V3 заносим значение целевой функции. Для этого используем встроенную математическую функцию СУММПРОИЗВ(). Далее ячейку с функцией V3 копируем в левые части ограничений, т.е. в ячейки V5:V7. Теперь воспользуемся надстройкой Поиск решения.
Результат решения
Находим значение седловой точки (цена игры):
Находим оптимальные стратегии первого игрока:
Если второй игрок с вероятностью 0,25 будет применять вторую стратегию, четвертую стратегию он применит с вероятностью 0,75, а вторую с третьей применять не будет, то при достаточно большом количестве игр с данной матрицей его выигрыш в среднем составит не менее 12.50.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 186; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.195.79 (0.007 с.) |

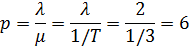
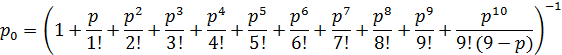
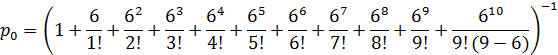
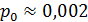
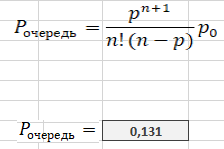
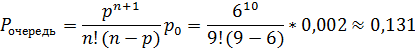
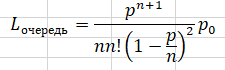

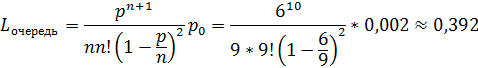
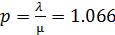
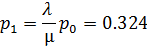
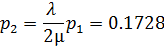
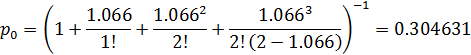
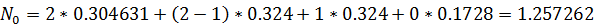
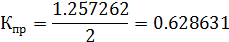
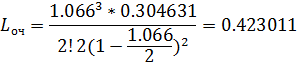
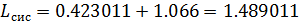
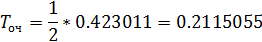
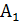 – стратегия первого игрока, он записывает число 3,
– стратегия первого игрока, он записывает число 3, 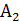 – стратегия первого игрока, он записывает число 4,
– стратегия первого игрока, он записывает число 4,  – стратегия первого игрока, он записывает число 9,
– стратегия первого игрока, он записывает число 9, 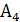 – стратегия первого игрока, он записывает число 8.
– стратегия первого игрока, он записывает число 8.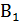 – стратегия второго игрока, он записывает число 3,
– стратегия второго игрока, он записывает число 3,  – стратегия второго игрока, он записывает число 4,
– стратегия второго игрока, он записывает число 4, 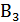 – стратегия второго игрока, он записывает число 9,
– стратегия второго игрока, он записывает число 9, 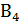 – стратегия второго игрока, он записывает число 8.
– стратегия второго игрока, он записывает число 8.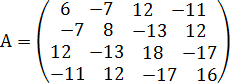
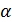 - гарантированный выигрыш игрока А называется нижней ценой игры. Стратегия, обеспечивающая получение выигрыша α, называется максиминной. Если первый игрок будет придерживаться своей максиминной стратегии, то у него есть гарантия, что он в любом случае выиграет не меньше α.
- гарантированный выигрыш игрока А называется нижней ценой игры. Стратегия, обеспечивающая получение выигрыша α, называется максиминной. Если первый игрок будет придерживаться своей максиминной стратегии, то у него есть гарантия, что он в любом случае выиграет не меньше α.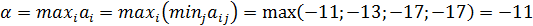
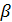 - гарантированный проигрыш игрока В называется верхней ценой игры. Стратегия, обеспечивающая получение проигрыша β, называется минимаксной. Если второй игрок будет придерживаться своей минимаксной стратегии, то у него есть гарантия, что он в любом случае проиграет не больше
- гарантированный проигрыш игрока В называется верхней ценой игры. Стратегия, обеспечивающая получение проигрыша β, называется минимаксной. Если второй игрок будет придерживаться своей минимаксной стратегии, то у него есть гарантия, что он в любом случае проиграет не больше 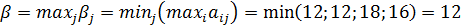
 , то платежная матрица не имеет седловую точку, т.е. она решается в смешанных стратегиях.
, то платежная матрица не имеет седловую точку, т.е. она решается в смешанных стратегиях.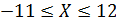
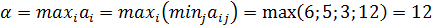
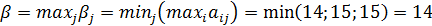
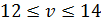
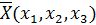 и
и 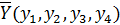 , где х1 – вероятность применения первым игроком первой стратегии, х2 – вероятность применения первым игроком второй стратегии, х3 – вероятность применения первым игроком третьей стратегии, а y1 – вероятность применении вторым игроком первой стратегии, y2 – вероятность применении вторым игроком второй стратегии, y3 – вероятность применении вторым игроком третьей стратегии, y4 – вероятность применении вторым игроком четвертой стратегии. Для вероятностей сумма равна 1.
, где х1 – вероятность применения первым игроком первой стратегии, х2 – вероятность применения первым игроком второй стратегии, х3 – вероятность применения первым игроком третьей стратегии, а y1 – вероятность применении вторым игроком первой стратегии, y2 – вероятность применении вторым игроком второй стратегии, y3 – вероятность применении вторым игроком третьей стратегии, y4 – вероятность применении вторым игроком четвертой стратегии. Для вероятностей сумма равна 1.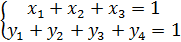
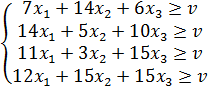

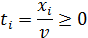
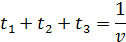
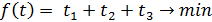
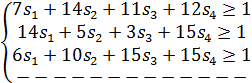 где,
где,