Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дизъюнктивные и конъюнктивные нормальные формыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Элементарными конъюнкциями называются конъюнкции переменных или их отрицаний, в которых каждая переменная встречается не более одного раза.
Дизъюнктивной нормальной формой (д.н.ф) называется формула, имеющая вид дизъюнкций элементарных конъюнкций. Например: F1= Формулу называют элементарной дизъюнкцией, если она является дизъюнкцией, возможно, одночленной, переменных и отрицаний переменных.
Формула находится в конъюнктивной нормальной форме (к.н.ф), если она является конъюнкцией элементарных дизъюнкций. Например: F2= Алгоритм построения ДНФ и КНФ 1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы (см. ПЗ №3). 2) Заменить знак отрицания, относящийся к выражениям типа
1) 2)
3) Избавиться от знаков двойного отрицания. 4) Применить если, нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
Пример 1. Приведите к ДНФ функцию f = Решение. Выразим логические операции «®» и «¯» через «Ù», «Ú», «-»: f = В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания: f = Используя закон дистрибутивности, приводим формулу к ДНФ: f =
Пример 2. Постройте КНФ функций и докажите тождественную истинность с помощью таблицы истинности: f(x1, x2, x3) = Решение. Процедура построения КНФ. 1. Исключаем связку «®» с помощью законов преобразования переменных:
2. Исключаем двойное отрицание с помощью правила 1) 2) 3. Для получения нормальной формы используем дистрибутивные законы:
f (x1, x2, x3) = 4. Проверка производится путем построения таблиц истинности для начальной (заданной) формулы и конечной (полученной в результате преобразований формулы).
Пример 3. Приведите к КНФ функцию f = Решение. Преобразуем формулу f к формуле, не содержащей ®: f = В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:
f = По закону дистрибутивности получим: f = Замечание. Если полученную формулу упростить, используя законы дистрибутивности, эквивалентности и поглощения, то получим:
Таким образом, мы получили формулу, которая является одновременно ДНФ и КНФ.
Двойственность Функция f1 (x1,…,x n) называется двойственной к функции f2 (x1,…,x n), если f1 (x1,…,x n) = Функция, двойственная самой себе, называется самодвойственной: Самодвойственными являются, например, функции Пример 4. Определите, является ли функция Т.к. f=f*, то функция самодвойственна.
Пример 5. Определите, является ли функция g = f =
Функция g двойственна f. Принцип двойственности для булевых функций. Если в формуле, представляющей функцию f, все конъюнкции заменить на дизъюнкции, дизъюнкции на конъюнкции, 1 на 0, 0 на 1, то получим формулу, представляющую функцию, двойственную f. Пример 6. Найти функцию, двойственную f= f*=
Пример 7. Перейти от ДНФ к КНФ. Задание можно выполнить, используя принцип двойственности для булевых функций. f КНФ = f* =
Если известна таблица истинности функции или, если функция задана векторно, то определить, самодвойственна ли она, можно используя следующий принцип. Нужно проверить, получается ли вторая половина вектора из первой путем отражения и последующей расстановки отрицаний над координатами.
Пример 8. Определить, являются ли самодвойственными функции f1 = 10110100; f2 = 10010110.
Вывод: f1 не является самодвойственной. f2 является самодвойственной.
Работу составила преподаватель Т.С. Пронина. Практическое занятие №6 1 Наименование работы: Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы. 2 Цель работы: Научиться представлять булевы функции в совершенных дизъюнктивных и конъюнктивных нормальных формах. Формирование ОК 2,3,8; овладение знаниями и умениями, необходимыми для освоения ПК 2.4. (спец. 09.02.03.), ПК 1.4, 2.4. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: «Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы».
4 Литература: 4.1 Конспект лекций по учебной дисциплине «Элементы математической логики», 2016 4.2 Приложение к ПЗ №6. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: Основная часть 6.1 Найдите СДНФ для ДНФ 6.2 Найдите СКНФ для КНФ 6.3 Функция трех переменных дана набором 0 и 1: f ( 6.4 Используя СДНФ, найдите булеву функцию, принимающую значение 1 на следующих наборах переменных: f (0,1,0) = f (1,0,1) = f (1,1,1) =1. 6.5 Функция трех переменных задана на единичном трехмерном кубе. Найдите ее СДНФ и СКНФ.
Вариативная часть 6.6 Найдите СДНФ и СКНФ для функций, заданных векторно. а) f = 11001001; б) f = 1; в) f = 0. 7 Порядок выполнения работы: Выполните практическую работу в соответствии с заданием (основная часть 6.1 – 6.5) и сдайте зачет. В случае получения зачета, выполните вариативную часть (6.6). 8 Содержание отчета: Решения задач в соответствии с заданием. 9 Контрольные вопросы: 1 Что такое СДНФ, СКНФ? 2 Как задать СДНФ и СКНФ на единичном N- мерном кубе? 3 Как построить СДНФ, СКНФ? 4 Всегда ли ДНФ можно привести к СДНФ, КНФ к СКНФ? 5 Можно ли построить для одной функции две и более СДНФ, две и более СКНФ?
Приложение к практическому занятию по ЭМЛ № 6
|
||||||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 463; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.135.89 (0.012 с.) |

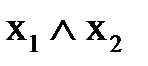 ;
;
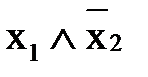 ;
;
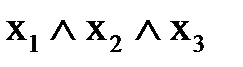 - являются элементарными конъюнкциями.
- являются элементарными конъюнкциями.

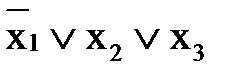 ;
;
 ;
;
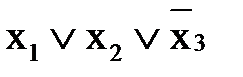 - являются элементарными дизъюнкциями.
- являются элементарными дизъюнкциями.
 x1 x2 x3
x1 x2 x3 или
или 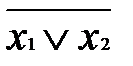 , знаками отрицания, относящимися к отдельным переменным на основании формул:
, знаками отрицания, относящимися к отдельным переменным на основании формул: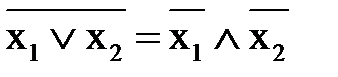 ;
;  .
.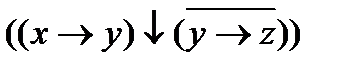 .
. .
.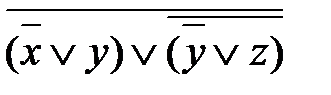 =
= 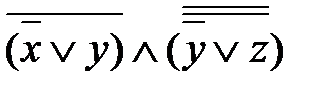 =
=  =
= 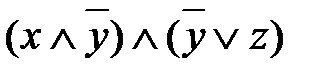 .
.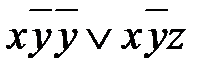 =
= 

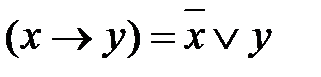 .
. и используем законы де Моргана:
и используем законы де Моргана:  =
= 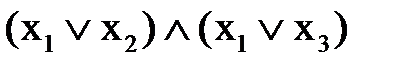
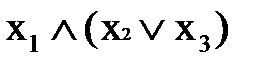 =
= 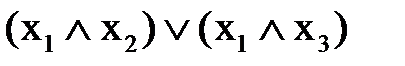
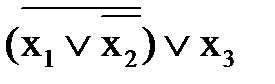 =
=  =
= 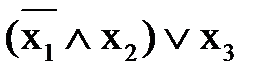 =
= 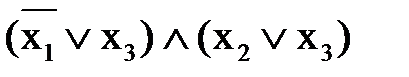 .
.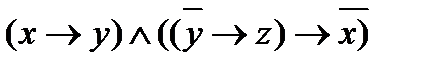 .
. =
=  .
.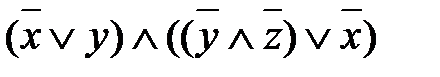 .
.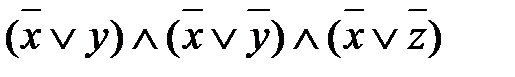 , являющейся КНФ.
, являющейся КНФ.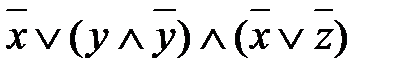 =
= 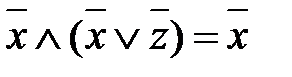 .
.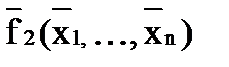 .
.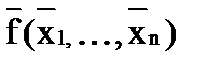 = f (x1,…,x n).
= f (x1,…,x n).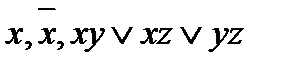 .
.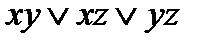 самодвойственной. f*=
самодвойственной. f*= 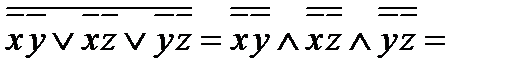
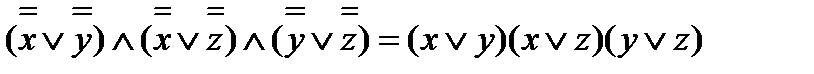 =
= 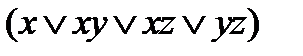
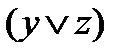 =
= 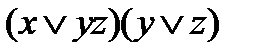 =
= 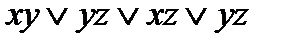 =
= 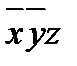 двойственной к
двойственной к 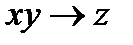 ?
?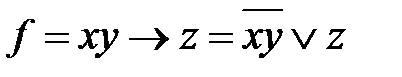 ;
;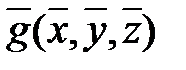 =
= 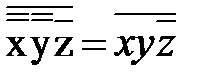 =
= 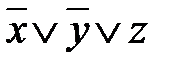 =
= 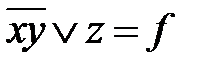 .
.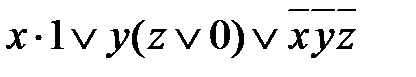
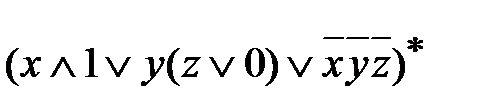 =
= 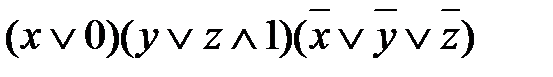
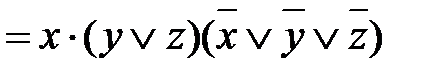
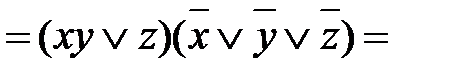
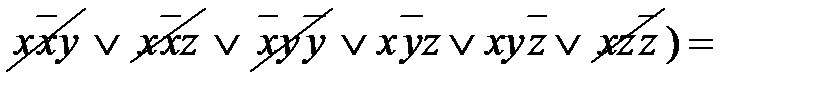
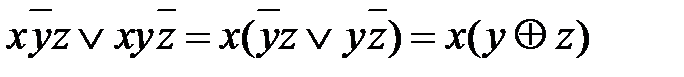 .
.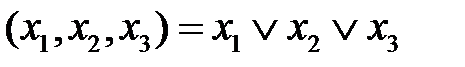
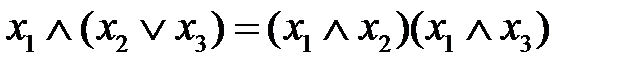 .
.
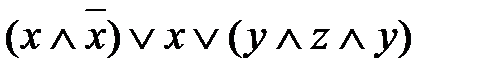 .
.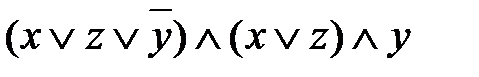 .
.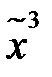 ) = 01011010. Найдите СДНФ и СКНФ для данной функции.
) = 01011010. Найдите СДНФ и СКНФ для данной функции.