
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перечень практических занятийСодержание книги
Поиск на нашем сайте
СБОРНИК ПРАКТИЧЕСКИХ ЗАНЯТИЙ по учебной дисциплине Элементы математической логики наименование учебной дисциплины (ПМ, МДК) номера занятий с ___ 1 __ по ___ 15 __ по программе утвержденной зам. директора по УВР А.В. Логвиновым Фамилия, И.О. « » 201г.
для специальности _09.02.03. – «Программирование в компьютерных системах» 09.02.04. – «Информационные системы» шифр и наименование специальности рассчитаны на 30 часов (часа). составил преподаватель _____ Т.С.Пронина, Н.Ю. Щербакова _____ Фамилия, И.О.
РАССМОТРЕНО на заседании цикловой комиссии «Естественнонаучные и общепрофессиональные дисциплины» наименование П(Ц)К Председатель _____________/_ Н.Ю. Щербакова ____/ подпись расшифровка подписи Протокол ___ 6 ___ от «__ 9 ___»_____ 01 ____ 2019 г. номер дата
Самара 2019 г.
Перечень практических занятий по дисциплине «Элементы математической логики»
Используемые сокращения Общие компетенции: ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес. ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество. ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность. ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития. ОК 5. Использовать информационно - коммуникационные технологии в профессиональной деятельности. ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями. ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий. ОК 8. Самостоятельно определить задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации. ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности. Профессиональные компетенции для специальности 09.02.03: ПК 1.1. Выполнять разработку спецификаций отдельных компонент. ПК 1.2. Осуществлять разработку кода программного продукта на основе готовых спецификаций на уровне модуля. ПК 2.4. Реализовывать методы и технологии защиты информации в базах данных. ПК 3.4. Осуществлять разработку тестовых наборов и тестовых сценариев.
Профессиональные компетенции для специальности 09.02.04: ПК 1.1. Собирать данные для анализа использования и функционирования информационной системы, участвовать в составлении отчетной документации, принимать участие в разработке проектной документации на модификацию информационной системы. ПК 1.2. Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности. ПК 1.4. Участвовать в экспериментальном тестировании информационной системы на этапе опытной эксплуатации, фиксировать выявленные ошибки кодирования в разрабатываемых модулях информационной системы.
ПК 2.3. Применять методики тестирования разрабатываемых приложений. ПК 2.4. Формировать отчетную документацию по результатам работ. Практическое занятие №1 1 Наименование работы: Алгебра высказываний. 2 Цель работы: Научиться составлять и читать высказывания. Формирование ОК 2,4,5; овладение знаниями и умениями, необходимыми для освоения ПК 1.1. (спец. 09.02.03.), ПК 1.1, 2.4. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: Высказывания простые и составные. 4 Литература: 4.1 Конспект лекций по учебной дисциплине «Элементы математической логики», 2016 4.2 Приложение к ПЗ №1. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: Основная часть 6.1 Определите, являются ли приведенные ниже предложения высказываниями. Объясните почему. В высказываниях определите истинностные значения: 1) Кто вы? 2) Прочтите эту главу до следующего занятия. 3) Это утверждение ложно. 4) Который час? 5) Целое число 1 есть наименьшее положительное целое число. 6) Если x = 3, то x2 = 6 7) Берегись автомобиля! 8) Новороссийск - южный город России. 9) Все четные числа делятся на 2. 10) Загрузите пакеты в машину. 11) Москва - столица Франции. 6.2 Пусть P, Q, R обозначают следующие высказывания: P: Путешествие на Марс является дорогостоящим. Q: Я совершу путешествие на Марс. R: У меня есть деньги. Запишите в символической форме такие высказывания: a) У меня нет денег, и я не совершу путешествие на Марс. b) У меня нет денег, и путешествие на Марс является дорогостоящим, или я совершу путешествие на Марс. c) Неверно, что у меня есть деньги, и я полечу на Марс. d) Путешествие на Марс не является дорогостоящим и я полечу на Марс, или путешествие на Марс является дорогостоящим, и я не полечу на Марс. 6.3 Пусть P, Q, R обозначают следующие высказывания: P: Эта игра очень трудна. Q: Я играю в шахматы. R: Игра в шахматы требует затрат времени. Интерпретируйте следующие выражения как обычные высказывания: а) QR б) в) (P г) P 6.4 Преобразуйте следующие высказывания к виду: «Если P, то Q» a) Он кентавр, только если он имеет шесть ног. b) Чтобы быть преуспевающим политиком, нужно быть избранным. c) Достаточно иметь деньги, чтобы быть популярным. 6.5 Приведите в качестве примеров 7 составных высказываний. Введите буквенные обозначения и запишите высказывания в символьной форме.
Вариативная часть: 6.6 Пусть P,Q,R – высказывания: P: Я умираю от жажды; Q: Мой стакан пуст; R: Сейчас 3 часа. Интерпретируйте следующие выражения как обычные высказывания: а) б) в) г) д) 6.7 Укажите, какие из следующих предложений являются высказываниями, определите, истинны они или ложны. а) Все треугольники равнобедренные. б) Вы были вчера в кино? в) Она играет в шахматы. 6.8 Для каждого из следующих высказываний найдите символическую форму. Воспользуйтесь буквенными обозначениями: X – «Джо умен» Y – «Джим глуп» Z – «Джо получит приз» а) Если Джо умен, а Джим глуп, то Джо получит приз. b) Джо получит приз в том и только в том случае, если он умен, или если Джим глуп. c) Если Джим глуп, а Джо не удается получить приз, то Джо не умен.
6.9 Пусть P, Q, R обозначают следующие высказывания: P: Он купит компьютер. Q: Он будет праздновать всю ночь. R: Он выиграет в лотерею. S: Он читает комиксы. T: Он любит научную фантастику. U: Он – ученый – информатик. Интерпретируйте следующие выражения как обычные высказывания: а) б) в) г) д) 6.10 Пусть P, Q, R обозначают следующие высказывания: P: Он удачлив. Q: Он популярен. R: Он богат. Интерпретируйте следующие выражения как обычные высказывания: а) б)
в) г) 7. Порядок выполнения работы: Выполните практическую работу в соответствии с заданиями (основная часть п.п. 6.1 – 6.5) и сдайте зачет. В случае получения зачета, выполните вариативную часть (п.п.6.6 – 6.10). 8 Содержание отчета: Решения задач в соответствии с заданием. 9 Контрольные вопросы: 1 Что называется высказыванием? 2 Приведите примеры, отличные от примеров конспекта лекций и приложения к ПЗ №1, повествовательных предложений, не являющихся высказываниями. 3 Как обозначаются высказывания? 4 Что используется в русском языке для построения составных высказываний из простых? 5 Что имеет значение в алгебре высказываний: смысловое значение или истинностное значение? 6 Как обозначаются и читаются логические связки: отрицание, конъюнкция, импликация, эквиваленция (эквивалентность)? Приложение к практическому занятию по ЭМЛ № 1
Составные высказывания В русском языке (как и в любом другом) из простых связных повествовательных предложений с помощью некоторых стандартных связок (конструкций) можно образовывать новые (составные) повествовательные предложения. Поставим в соответствие высказыванию логическую переменную x, которая принимает значение 1, если высказывание истинно, и 0 если высказывание ложно. Составные высказывания будем получать из простых с помощью логических операций: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность, которые осуществляются при помощи логических связок:
Пример. Пусть А, В обозначают следующие высказывания: A: «Солнце светит», В: «Трава зеленеет». Тогда 1) 2) 3) 4)
Работу составила преподаватель Т.С. Пронина
Практическое занятие №2 1 Наименование работы: Логические операции. 2 Цель работы: Научиться составлять и читать высказывания, использовать логические операции в высказываниях, таблицах истинности. Формирование ОК 1, 3- 5, 9; овладение знаниями и умениями, необходимыми для освоения ПК 1.1. (спец. 09.02.03.), ПК 1.1, 1.2, 2.4. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: Логические операции. 4 Литература: 4.1 Конспект лекций по учебной дисциплине «Элементы математической логики», 2016 4.2 Приложение к ПЗ №2. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: Основная часть 6.1 Постройте таблицы истинности для пунктов задания 6.2 и 6.3 ПЗ № 1. Укажите тавтологии и опровержения, если таковые имеются. 6.2 Постройте таблицы истинности для следующих выражений и определите, являются ли они тавтологией или противоречием (опровержением). 1) 2) 3) 6.3 Проверьте, пользуясь таблицами истинности, эквивалентность следующих высказываний. Определите, являются ли они противоречием или тавтологией. а) б) 6.4 В каких случаях приведенные ниже данные противоречивы? 1) A= 1, 2) A= 0, 3) A= 1, 4) A= 0, Вариативная часть: 6.5 Известно, что а) б) в) 6.6 Докажите тождественную истинность выражения 6.7 При каких значениях переменных P,Q,R следующие выражения ложны? Объясните, почему. 1) 2) 3) 7 Порядок выполнения работы: Выполните практическую работу в соответствии с заданиями (основная часть п.п. 6.1 – 6.4) и сдайте зачет. В случае получения зачета, выполните вариативную часть (п.п.6.5 – 6.6). 8 Содержание отчета: Решения задач в соответствии с заданием. 9 Контрольные вопросы: 1 Что такое тавтология, опровержение? 2 Постройте таблицы истинности для логических операций: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция. 3 В каком порядке при отсутствии скобок выполняются логические операции? 4 Какие формулы алгебры высказываний являются эквивалентными?
Приложение к практическому занятию по ЭМЛ № 2
Тавтология и противоречие Высказывание, истинное во всех случаях, называется логически истинным, или тавтологией. Каждое высказывание вида Высказывание, построенное так, что оно ложно в любом случае, называется логически ложным, или противоречием (опровержением). Например, высказывание: «Она движется в направлении Самары и она не движется в направлении Самары» всегда ложно, т.к. нельзя делать одновременно и то, и другое, следовательно, это противоречие.
Пример тавтологии
Пример противоречия
Работу составила преподаватель Т.С. Пронина
Практическое занятие №3 1 Наименование работы: Решение задач на доказательство. 2 Цель работы: Научиться производить требуемые доказательства с помощью таблиц истинности. Формирование ОК 1, 3- 5, 9; овладение знаниями и умениями, необходимыми для освоения ПК 1.1., 2.4. (спец. 09.02.03.), ПК 1.1, 1.2, 2.4. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: Логические операции. Литература 4.1 Конспект лекций по учебной дисциплине ЭМЛ, 2016 4.2 Приложение к ПЗ № 3. Приложение к практическому занятию по ЭМЛ № 3 Кроме отрицания, конъюнкции, дизъюнкции, эквиваленции и импликации существуют другие виды логических операций: Å - сумма по модулю два; ô - штрих Шеффера; ¯ - стрелка Пирса. Их таблицы истинности приведены ниже.
Штрих Шеффера, или антиконъюнкция, по определению
Стрелка Пирса, или антидизъюнкция, по определению X¯Y=
Сумма по модулю два, или антиэквивалентность, по определению XÅ Y =
С помощью таблиц истинности можно проверить эквивалентность высказываний. Высказывания эквивалентны, если их таблицы истинности равны. Пример 1. С помощью таблиц истинности проверить, являются ли эквивалентными высказывания: A= Решение.
Так как значения для высказываний A и B в таблице истинности не совпали, то высказывания не эквивалентны.
Логическое следование Иногда бывает желательно рассмотреть взаимоотношение двух высказываний. Наиболее интересное из таких отношений имеет место, когда из одного высказывания логически следует другое. Если из X следует Y, мы говорим также, что Y является следствием X или что Y логически выводимо из X.. Исходя из анализа логических возможностей для пары высказываний X и Y, отношение следствия можно охарактеризовать таким образом: из X следует Y, если Y истинно всякий раз, когда истинно X, т.е. если Y истинно во всех логически возможных случаях, в которых X истинно. В случаях составных высказываний, имеющих одни и те же компоненты, таблицы истинности дают удобный метод для проверки того, имеет ли место отношение следствия. Следующая таблица иллюстрирует этот метод:
Высказывание
Работу составила преподаватель Т.С. Пронина Практическое занятие № 4 1 Наименование работы. Упрощение формул логики с помощью равносильных преобразований. 2 Цель практической работы: Научиться упрощать формулы логики с помощью равносильных преобразований. Формирование ОК 2,3,5, 6; овладение знаниями и умениями, необходимыми для освоения ПК 1.1. (спец. 09.02.03.), ПК 1.1, 1.2, 2.3. (спец. 09.02.04.). 3 Подготовка к занятию: Повторить законы логики и их применение для равносильных преобразований. Литература 4.1 Конспект лекций по учебной дисциплине «Элементы математической логики», 2016 4.2 Приложение к ПЗ №4. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: Основная часть 6.1. Произведите тождественное преобразование формул: a) б) в) г) д) е) ж) 6.2. Проверьте правильность выполнения преобразований путем построения таблиц истинности целесообразно для правой и левой части полученных тождеств. Примечание. Для проверки правильности преобразования путем построения таблиц истинности целесообразно использовать программу DiTable. Вариативная часть: 6.3 Произведите тождественное преобразование формул. Проверьте правильность выполнения преобразований путем построения таблиц истинности. а) б) в) г) 7 Порядок проведения практического занятия: Выполните практическую работу в соответствии с заданиями (основная часть 6.1 – 6.2) и сдайте зачет. В случае получения зачета выполните вариативную часть (6.3). 8 Содержание отчета: Решение примеров в соответствии с заданием. 9 Контрольные вопросы: 9.1 Перечислите виды булевых (логических) операций над высказываниями и сформулируйте их определение. 9.2 Для каких операций выполняются, как записываются и формулируются нижеперечисленные законы логики: а) идемпотентности; б) коммутивности, ассоциативности, дистрибутивности; в) де Моргана; г) нуля и единицы; д) исключенного третьего? 9.3 Как от операций импликация, эквиваленция, сложение по модулю два, штрих Шеффера, стрелка Пирса перейти к операциям булева базиса. Приложение к практическому занятию по ЭМЛ № 4
Под упрощением подразумевается преобразование исходного выражения в эквивалентное, содержащее меньше символов, чем исходное. Приложение к практическому занятию по ЭМЛ № 5 Двойственность Функция f1 (x1,…,x n) называется двойственной к функции f2 (x1,…,x n), если f1 (x1,…,x n) = Функция, двойственная самой себе, называется самодвойственной: Самодвойственными являются, например, функции Пример 4. Определите, является ли функция Т.к. f=f*, то функция самодвойственна.
Пример 5. Определите, является ли функция g = f =
Функция g двойственна f. Принцип двойственности для булевых функций. Если в формуле, представляющей функцию f, все конъюнкции заменить на дизъюнкции, дизъюнкции на конъюнкции, 1 на 0, 0 на 1, то получим формулу, представляющую функцию, двойственную f. Пример 6. Найти функцию, двойственную f= f*=
Пример 7. Перейти от ДНФ к КНФ. Задание можно выполнить, используя принцип двойственности для булевых функций. f КНФ = f* =
Если известна таблица истинности функции или, если функция задана векторно, то определить, самодвойственна ли она, можно используя следующий принцип. Нужно проверить, получается ли вторая половина вектора из первой путем отражения и последующей расстановки отрицаний над координатами.
Пример 8. Определить, являются ли самодвойственными функции f1 = 10110100; f2 = 10010110.
Вывод: f1 не является самодвойственной. f2 является самодвойственной.
Работу составила преподаватель Т.С. Пронина. Практическое занятие №6 1 Наименование работы: Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы. 2 Цель работы: Научиться представлять булевы функции в совершенных дизъюнктивных и конъюнктивных нормальных формах. Формирование ОК 2,3,8; овладение знаниями и умениями, необходимыми для освоения ПК 2.4. (спец. 09.02.03.), ПК 1.4, 2.4. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: «Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы». 4 Литература: 4.1 Конспект лекций по учебной дисциплине «Элементы математической логики», 2016 4.2 Приложение к ПЗ №6. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: Основная часть 6.1 Найдите СДНФ для ДНФ 6.2 Найдите СКНФ для КНФ 6.3 Функция трех переменных дана набором 0 и 1: f ( 6.4 Используя СДНФ, найдите булеву функцию, принимающую значение 1 на следующих наборах переменных: f (0,1,0) = f (1,0,1) = f (1,1,1) =1. 6.5 Функция трех переменных задана на единичном трехмерном кубе. Найдите ее СДНФ и СКНФ.
Вариативная часть 6.6 Найдите СДНФ и СКНФ для функций, заданных векторно. а) f = 11001001; б) f = 1; в) f = 0. 7 Порядок выполнения работы: Выполните практическую работу в соответствии с заданием (основная часть 6.1 – 6.5) и сдайте зачет. В случае получения зачета, выполните вариативную часть (6.6). 8 Содержание отчета: Решения задач в соответствии с заданием. 9 Контрольные вопросы: 1 Что такое СДНФ, СКНФ? 2 Как задать СДНФ и СКНФ на единичном N- мерном кубе? 3 Как построить СДНФ, СКНФ? 4 Всегда ли ДНФ можно привести к СДНФ, КНФ к СКНФ? 5 Можно ли построить для одной функции две и более СДНФ, две и более СКНФ?
Приложение к практическому занятию по ЭМЛ № 6 Единичный n -мерный куб Множество двоичных наборов длины n образует n – мерный булев (или двоичный) куб, который называют также единичным n – мерным кубом и обозначают Вn или Наборы Такой n – мерный куб будет однозначно задавать любую булеву функцию
рис.1
Пример 5. Функция трех переменных задана на единичном трехмерном кубе. Найдите ее СДНФ.
СДНФ будет выглядеть так:
Работу составила преподаватель Т.С. Пронина
Практическое занятие №7 1 Наименование работы: Минимизация нормальных форм. 2 Цель работы: Научиться минимизировать СКНФ и СДНФ с помощью карты Карно и алгебраических преобразований. Формирование ОК 1,2,3; овладение знаниями и умениями, необходимыми для освоения ПК 2.4, 3.4. (спец. 09.02.03.), ПК 1.4, 2.4. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: Минимизация нормальных форм. 4 Литература: 4.1 Конспект лекций по учебной дисциплине «Элементы математической логики», 2016 4.2 Приложение к ПЗ №7. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: Основная часть 6.1 Минимизируйте СДНФ а) б) в) г) 6.2 Определите СДНФ и минимизируйте ее с помощью карты Карно и логических преобразований. Сравните результаты, если f (x,y,z) = 6.3 Минимизируйте СДНФ функций, заданных набором переменных. а) f (0,0,0) = f (0,0,1) = f (1,0,1) = f (1,1,1) =1 б) f (0,0,0) = f (1,1,1) = f (1,1,0) = 0 в) f (1,0,0) = f (0,1,1) = f (0,1,0) = 0 г) f (0,1,1) = f (0,1,0) = f (1,0,1) = f (1,1,1)= 0 д) f (0,1,1) = f (1,0,0) = f (1,0,1) = 1 Вариативная часть 6.4 Найдите СДНФ функции:
6.5 Перейдите от СКНФ к СДНФ, используя закон двойственности, минимизируйте ее:
6.6 Минимизируйте СДНФ функций f1, f2, f3 (см. таблицу 1). 1) методом карт Карно; 2) с помощью логических преобразований.
Таблица 1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 301; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.3.102 (0.017 с.) |

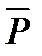

 R)
R)  Q
Q Q
Q  R
R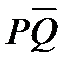

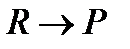
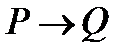
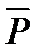
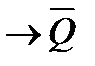
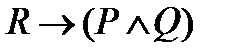 ;
;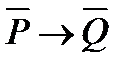 ;
;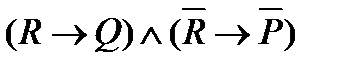 ;
;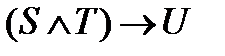 ;
;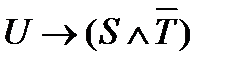 .
.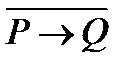
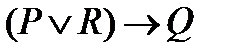
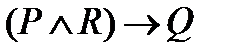
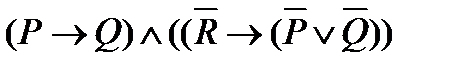
 , Ù, Ú, ®, «.
, Ù, Ú, ®, «.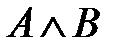 можно интерпретировать как «Солнце светит, и трава зеленеет».
можно интерпретировать как «Солнце светит, и трава зеленеет».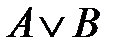 «Солнце светит, или трава зеленеет».
«Солнце светит, или трава зеленеет».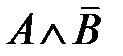 «Солнце светит, но трава не зеленеет».
«Солнце светит, но трава не зеленеет».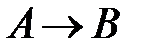 «Если солнце светит, то трава зеленеет».
«Если солнце светит, то трава зеленеет».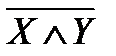 ;
;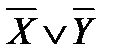 ;
;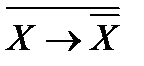 .
.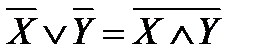 ; в)
; в) 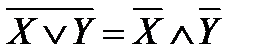 ;
;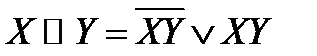 ; г)
; г) 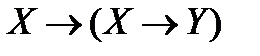 .
. 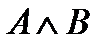 = 1
= 1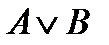 = 0
= 0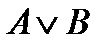 = 1
= 1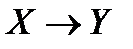 имеет значение 1. Что можно сказать о значениях нижеприведенных выражений? Объясните, почему?
имеет значение 1. Что можно сказать о значениях нижеприведенных выражений? Объясните, почему?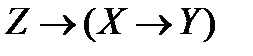 ;
;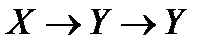 ;
;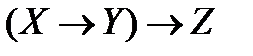 .
.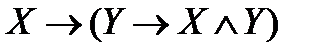
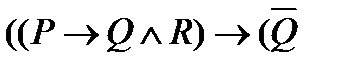
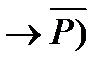
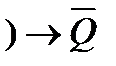 ;
;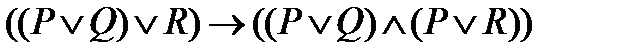 ;
;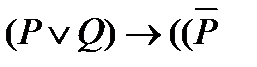
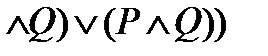
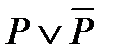 - тавтология. Например: «Быть или не быть».
- тавтология. Например: «Быть или не быть».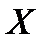
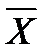
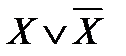

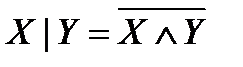
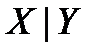
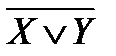
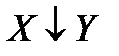
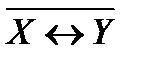 .
.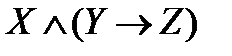 и B=
и B= 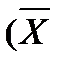
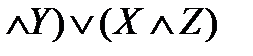 .
.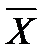
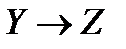
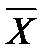
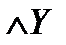
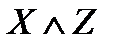

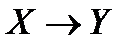

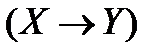 (XÚY);
(XÚY);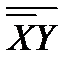 (XÚY);
(XÚY);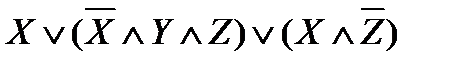 ;
;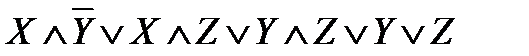 ;
;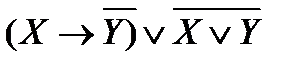 ;
;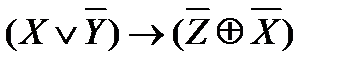 ;
;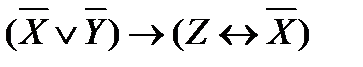 .
.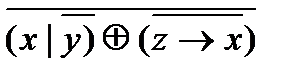 ;
;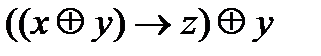 ;
;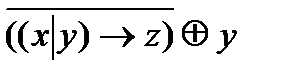 ;
;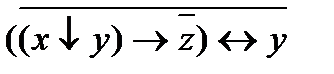 ;
;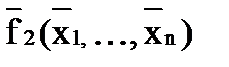 .
.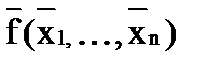 = f (x1,…,x n).
= f (x1,…,x n).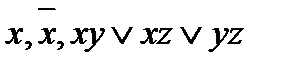 .
.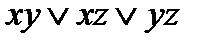 самодвойственной. f*=
самодвойственной. f*= 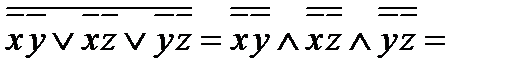
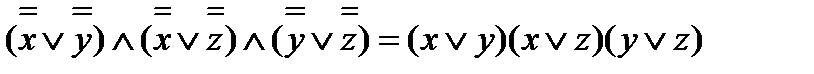 =
= 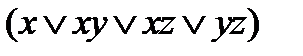
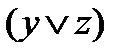 =
= 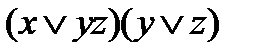 =
= 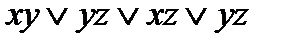 =
= 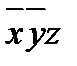 двойственной к
двойственной к 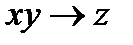 ?
?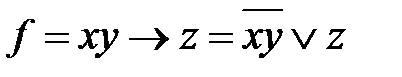 ;
;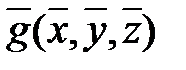 =
= 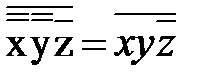 =
= 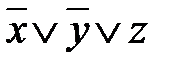 =
= 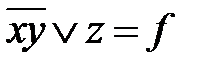 .
.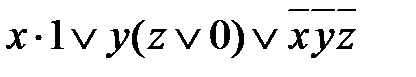
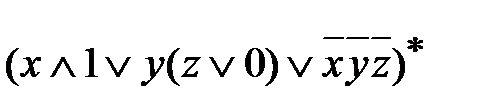 =
= 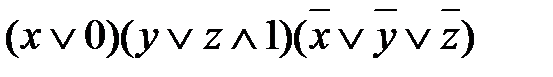
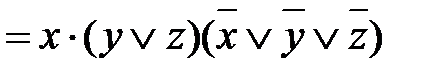
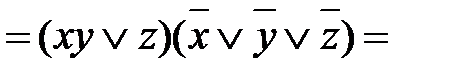
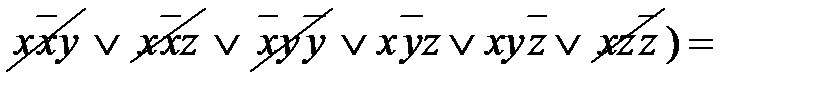
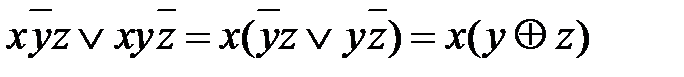 .
.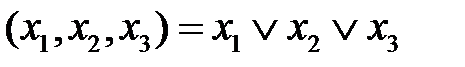
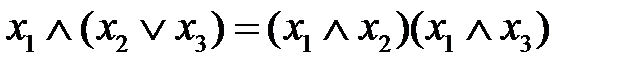 .
.
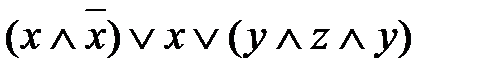 .
.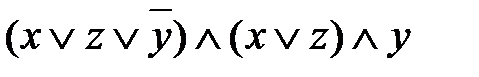 .
.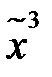 ) = 01011010. Найдите СДНФ и СКНФ для данной функции.
) = 01011010. Найдите СДНФ и СКНФ для данной функции.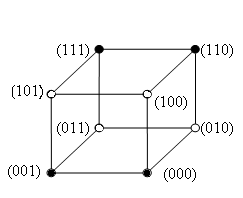
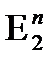 .
.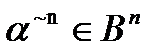 называют вершинами куба Вn . Каждой вершине n – мерного единичного куба можно приписать конкретное значение 0 или 1, которое принимает булева функция при соответствующем наборе аргументов (векторов
называют вершинами куба Вn . Каждой вершине n – мерного единичного куба можно приписать конкретное значение 0 или 1, которое принимает булева функция при соответствующем наборе аргументов (векторов 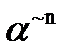 ). Если значение функции равно 0, то точка не рисуется (выкалывается). Если же значение функции равно 1, то точка рисуется – выделяется полужирно.
). Если значение функции равно 0, то точка не рисуется (выкалывается). Если же значение функции равно 1, то точка рисуется – выделяется полужирно.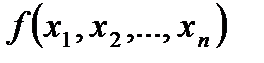 . Например, для двух переменных геометрическая интерпретация булевой функции будет на плоскости иметь вид квадрата или «двумерного куба» (рис. 1), а для трех переменных – трехмерного куба – куба в пространстве (рис. 2).
. Например, для двух переменных геометрическая интерпретация булевой функции будет на плоскости иметь вид квадрата или «двумерного куба» (рис. 1), а для трех переменных – трехмерного куба – куба в пространстве (рис. 2).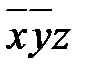
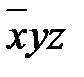
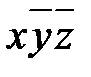
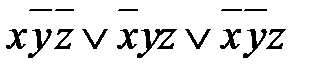 .
.
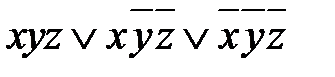
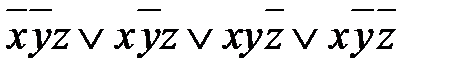
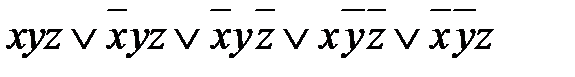
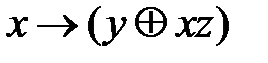
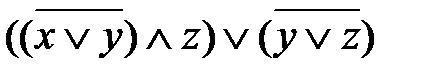 , минимизируйте её.
, минимизируйте её.



