
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логические операции, составные высказывания и диаграммы Эйлера-Венна⇐ ПредыдущаяСтр 11 из 11
Объединение множеств А и В можно представить выражением АÈВ. Это соответствует логической операции дизъюнкция. Диаграмма Эйлера-Венна для объединения изображена на рис.6, а таблица истинности логической операции высказывания представлена таблицей 1.
АÈВ Таблица 1
рис.6
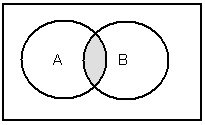
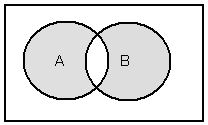
Пересечение множеств А и В можно представить выражением АÇВ. Это соответствует логической операции конъюнкция. Диаграмма Эйлера-Венна для пересечения изображена на рис.7, а таблица истинности логической операции конъюнкция высказываний А, В представлена таблицей 2.
АÇВ Таблица 2
рис.7
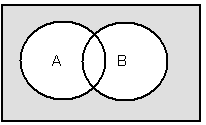
Дополнение множества А можно представить выражением
рис. 8
На рис.10 и рис.11 приведены диаграммы двух логических операций: стрелки Пирса (табл. 4) и штриха Шеффера (табл.5). Эти диаграммы дополняют объединение и пересечение множеств, т.к. А¯В =
А¯В Таблица 4
рис.10
А|В Таблица 5
рис.11
Существует тесная связь между множествами – с одной стороны, и высказываниями – с другой, а также между операциями над множествами, с одной стороны, и операциями образования составных высказываний – с другой. Множество истинности двух высказываний X и Y показаны на диаграмме Эйлера-Венна (рисунок 9). Здесь отмечены различные логические возможности этих высказываний.
рис. 9
Связь между высказыванием и его множеством истинности создает возможность «перевода» любой задачи, относящейся к составным высказываниям, в задачу теории множеств. Возможно также и обратное: если поставлена какая-то задача, касающаяся множеств, то универсальное множество можно себе представить как некоторое множество логических возможностей, подмножества которого являются множествами истинности некоторых высказываний. Следовательно, задачу, относящуюся к множествам, можно также «перевести»на язык составных высказываний. Разность множеств А и В можно представить выражением А/В. Это соответствует логической операции
А/В Таблица 6
рис.12
Импликация X®Y эквивалентна дизъюнкции
А®В Таблица 7
рис.13
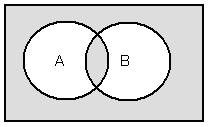
Симметрическую разность множеств А и В можно представить выражением АDВ или (А/В)È(В/А). Это соответствует логической операции АÅВ. Диаграмма Эйлера-Венна для симметрической разности изображена на рис.14, а таблица истинности логической операции высказывания представлена таблицей 8.
АDВ Таблица 8
рис.14
На рис.15 приведена диаграммы эквиваленции (табл.9). Эквиваленция является дополнением симметрической разности (суммы по модулю два), т.к. А~В=
А~В Таблица 9
рис.15
Работу составила преподаватель Т.С. Пронина
Практическое занятие №13 1 Наименование работы: Бинарные отношения. 2 Цель работы: Научиться исследовать отношения. Формирование ОК 1,3,4,5; овладение знаниями и умениями, необходимыми для освоения ПК 1.1. (спец. 09.02.03.), ПК 1.4. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: Бинарные отношения. 4 Литература: 4.1 Конспект лекций по учебной дисциплине «Элементы математической логики», 2016 4.2 Приложение к ПЗ №13. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: Основная часть 6.1 Равны ли следующие кортежи? Объясните, почему? 1) 2) 3) 4)
6.2 На множестве A= {2, 3, 4, 5, 6, 7, 8} отношение R определено как R={(x, y):x, yÎ A, x Задайте отношение. Укажите область определения бинарного отношения DR = {x:(x, y)ÎR} и область значений PR = {y:x, yÎR}. Найдите обратное бинарное отношение R-1 = {(y, x):x, yÎR}.
6.3 На множестве натуральных чисел заданы отношения R и S R= {(1, 7), (4, 6), (5, 6), (2, 8)}; S= {(6, 10), (6, 11), (7, 10), (8, 13)}. Определите а) S o R б) R-1 o S-1 в) S o S-1 г) S-1o S
6.4 На множестве A= {a, b, c, d, e} заданы отношения S, T, U S = {(a, a), (a, b), (b, c), (b, d), (c, e), (e, d), (c, a)}; T = {(a, b), (b, a), (b, c), (b, d), (e, e), (d, e), (c, b)}; U = {(a, b), (b, c), (b, b), (e, e), (b, a), (c, b), (d, d), (a, c), (c, a)}. Постройте матрицы отношений MS, MT, Mu, исследуйте отношения на рефлективность, симметричность, антисимметричность и транзитивность. Геометрически изобразите бинарное отношение R. Вариативная часть 6.5 Найдите область определения и множество значений отношений: а) б) в)
6.6Пусть A = B = C = D = Пусть R = S = T = Определите отношения: а) R-1 и S-1; б) S o R; в) S o S-1 и S-1o S; г) R-1 o S-1; д) T o (S o R); е) T o S; ж) (T o S) o R.
6.7 На декартовом квадрате множества А = Вышеуказанные свойства докажите.
7 Порядок выполнения работы: Выполните практическую работу в соответствии с заданиями (основная часть 6.1 – 6.4) и сдайте зачет. В случае получения зачета, выполните вариативную часть (6.5 – 6.7). 8 Содержание отчета: Решения задач в соответствии с заданием. 9 Контрольные вопросы: 1 Чем отличается кортеж от множества? 2 Приведите определение бинарного отношения. 3 В каком случае бинарное отношение называется рефлексивным, симметричным, транзитивным, эквивалентным? 4 Перечислите способы задания бинарного отношения. 5 Как найти обратное отношение? 6 Как найти композицию отношений? 7 Что является областью определения бинарных отношений; областью истинности? Приложение к практическому занятию по ЭМЛ № 13 Кортежи Определение. Пусть даны множества X1, X2, …, Xn. Кортежем длины n, составленным из элементов этих множеств, называется конечная последовательность α = <x1, x2, …xn>, где для всех k, 1£ k £n, имеем xk Элемент xk называется k-й координатой или k-й компонентной кортежа α. Два кортежа равны в том и только в том случае, когда они имеют одинаковую длину, причем их координаты, стоящие на местах с одинаковыми номерами, равны, т.е. кортежи α = <x1, …xm>, b = <y1, …yn> равны только в том случае, когда m = n, причем xk = yk для всех 1£ k £n. Кортежи длины два называют упорядоченными парами, длины три – упорядоченными тройками, …, длины n – упорядоченными n – ками. Для краткости речи слово «упорядоченные» часто опускают.
Кортеж, не содержащий ни одной координаты, т.е. кортеж длины 0, называется пустым. Основные отличия понятий кортежа и множества следующие: а) в множестве порядок элементов не играет роли, а кортежи, отличающиеся порядком элементов, различны, даже в случае, когда они имеют одинаковый состав; б) в множестве все элементы различны, а в кортеже координаты могут повторяться. В дальнейшем, чтобы различать множества и кортежи, будем элементы множества заключать в фигурные скобки, а координаты кортежа – в угловые. Пример 1. Сравните кортежи: а) Решение. а) Кортежи б) кортежи в) кортежи Бинарные отношения Пусть A и B два конечных множества. Бинарным отношением между элементами множеств A и B называется любое подмножество R множества A х B, т.е. R Ì A х B. Если R – бинарное отношение (т.е. множество пар), то говорят, что параметры x и y связаны бинарным отношением R, если пара <x, y> является элементом R, т.е. <x, y> Î R. Высказывание: «предметы x и y связаны бинарным отношением R» записывают в виде: x R y. Таким образом, x R y «<x, y> Î R. Если R Ì A x A, то говорят, что бинарное отношение определено на множестве A или на квадрате множества А. Областью определения бинарного отношения R называется множество, состоящее из таких x, для которых <x, y> Î R хотя бы для одного y. Область определения бинарного отношения будем обозначать DR. Областью значений бинарного отношения R называется множество всех y, для которых <x, y> Î R хотя бы для одного x. Область значений бинарного отношения будем обозначать PR.
Пример 2. Найдите область определения и область значений отношения R = Решение. DR. =
Пусть R Ì A х B есть отношение на A х B. Тогда отношение R-1 на B х A определяется следующим образом: R-1 = Другими словами,
Пример 3. Бинарные отношения R заданы множеством упорядоченных пар R =
R-1 =
Пусть R Í A х B - отношение на A х B, а S Í B х C – отношение S на B х C. Композицией отношений S и R называется отношение T Í A х C, определенное таким образом: T = Это множество обозначается T = S o R. Пример 4. Пусть А = {1, 2, 3}, B = {x, y}, а С = {ð, O, D, *}, и пусть отношения R на A х B и S на B х C заданы в виде:
Тогда
Поскольку из (1,х) Î R и (х, ð) Î S следует (1, ð) Î S o R; из (1,х) Î R и (х, ∆ÎS) Î S следует (1, ∆) Î S o R; из (1,y) Î R и (y, O) Î S следует (1, O) Î S o R; . . . из (3,х) Î R и (х, D) Î S следует (3, D) Î S o R;
Свойства бинарных отношений 1) Бинарное отношение R на непустом множестве A называется рефлексивным, если 2) Бинарное отношение R на непустом множестве A называется антирефлексивным, если 3) Бинарное отношение R на непустом множестве А называется симметричным, если 4) Бинарное отношение R на непустом множестве A называется антисимметричным, если из того, что выполняется условие Не путать с асимметричными, в которых В асиметричных отношениях из 2-ух отношений 5) Бинарное отношение R на непустом множестве A называется транзитивным если Пример. Если 2<3 и 3<4, то 2<4 Транзитивны отношения «быть параллельным», «быть больше», «быть равным». Пример
Пример. Бинарное отношение R антитранзитивно, если для любых трех элементов не выполняется условие транзитивности на множестве прямых ( Рефлексивное, транзитивное и симметричное бинарное отношение R на множестве А называется эквивалентностью на А.
Пример 5. Определите свойства бинарных отношений «х делит y» на множестве натуральных чисел. Поскольку х всегда делит сам себя, то это отношение рефлексивно. Оно, конечно, не симметрично, поскольку, напрмер, 2 является делителем 6, но не наоборот: 6 не делит 2. Проверим, что отношение делимости транзитивно. предположим, что х делит y, а y в свою очередь делит z. Тогда из первого предположения вытекает, что y = mx для некоторого натурального числа m, а из второго – z = ny, где n – натуральное число. Следовательно, z = ny = (nm) x, т.е. x делит z. Значит данное отношение транзитивно.
Наконец, наше отношение антисимметрично, поскольку из предположений: x делит y и y делит x немедленно вытекает, что y = x.
Работу составила преподаватель Т.С. Пронина
Практическое занятие №14 1 Наименование работы: Отображения. Функции. 2 Цель работы: Научиться выявлять отображения, исследовать функции. Формирование ОК 1,3,4,5; овладение знаниями и умениями, необходимыми для освоения ПК 1.1, 1.2. (спец. 09.02.03.), ПК 1.4, 2.3. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: Отображения. Функции. 4 Литература: 4.1 Конспект лекций по учебной дисциплине «Элементы математической логики», 2016 4.2 Приложение к ПЗ №14. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: Основная часть 6.1 Определите, являются ли отношения функциями. Ответ поясните. а) R= {(1,2), (2,3),(3,2)} б) S= {(1,2), (1,3), (2,3)} в) T= {x, x2 -2x -3: xÎR} г) U=(1,а), (1,в), (2,а) 6.2 На одном рисунке постройте график выражения и обратное отношение. а) y= 3x-1 б) y= (x-1)2 при x ³1 6.3 Является ли функция f(x)=x2, заданная на множестве действительных чисел, инъективной? Почему? Изменится ли ответ, если функцию определить на множестве натуральных чисел? 6.4 Заданы множества: A= {a1, a2, a3}, B= {b1, b2, b3}, а также их отношение: R= {(a1, b1), (a2, b2), (a3, b3)}. Определите, является ли данное отношение сюръективным, инъективным, биективным? Имеет ли заданное отношение R обратное R-1? 6.5 Задано множество: A= {1, 2, 3, 4} и на его квадрате задано отношение R= {(1,4), (2,3), (3,2), (4,1)}. Определите, является данное отношение биекцией? Имеет ли оно обратное отношение R-1? 6.6 Заданы: X - множество пальто; Y - множество крючков; Определите, при каких условиях размещения пальто на крючках можно получить инъективное, сюръективное, биективное отображения? Вариативная часть 6.7 Найдите область определения DR и область значения PR отношения R= {(1,5), (1, 6), (1,7)}. Является ли данное отношение функцией? 6.8 Среди следующих отображений укажите сюръективные отображения: 1) X - множество кругов, Y - множество действительных чисел, каждому кругу сопоставляется его площадь; 2) X - множество кругов, Y- множество положительных действительных чисел, каждому кругу сопоставляется его площадь; 3) X= {x: -3£ x £ 5}, Y= R, f:x ®x2 (R - множество действительных чисел); 4) X= {x: -3£ x £5}, Y= {x:0 £x £25}, f: x ® x2. 6.9 Отношение R задано на декартовом произведении множеств В и Р, где В – множество книг в магазине, Р – множество цен. Пара (х, у) принадлежавшей R, только и если только книга х имеет цену у. Является ли R функцией? Если да. то является ли данная функция сюръективной, инъективной, биективной? 6.10. Является ли отношение R = {(1,4), (2,3), (3,2), (4,1)} заданное на декартовом квадрате множества А = {1,2,3,4} биективным отображением? 7 Порядок выполнения работы: Выполните практическую работу в соответствии с заданиями (основная часть 6.1 – 6.6) и сдайте зачет. В случае получения зачета, выполните вариативную часть (6.7– 6.10). 8 Содержание отчета: Решения задач в соответствии с заданием. 9 Контрольные вопросы: 1 Что является отображением множества А во множестве В? 2 Что такое функция? 3 Приведите определения инъекции, сюръекции, биекции.
Приложение к практическому занятию по ЭМЛ № 14 Бинарное отношение f Í A´B называется функцией или отображением из множества А в множество В, если Df = A, Rf ÍB и из (x,y1)Îf, (x,y2)Îf следует, что y1 = y2. Область определения функции обозначается Df,область значений – Rf. Определяются они так же, как для бинарных отношений. Если же вместо Df=A выполняется Df,ÍA, то f называется частичной функцией. В этом случае говорят, что функция f задана на множестве А со значениями во множестве В и осуществляет отображение множества А во множество В. Функция f из А в В обозначается через f: A®B или A®B. Функция называется инъективной (равнозначной), если отношение f -1 является частичной функцией, т.е для любых элементов x1,x2ÎD из x1 ¹ x2 следует f(x1) ¹ f(x2). Функция f: A®B называется функцией А на В или сюръективной функцией, если Rf =B. Для сюръективной функции для любого yÎB существует xÎA такой, что f(x)= y. Функция f называется биективной, если она одновременно сюръективна и инъективна. В этом случае говорят, что f осуществляет взаимно однозначное соответствие между множествами А и В. Пример 1. На рис.1 показаны функции fi: A®B, i=
рис.1
Отображение f: A®B имеет обратное отображение f-1: B®A тогда и только тогда, когда f - биекция, т.е если f: A«B, то f-1: B«A, f °f-1= idA, f-1 °f= idB.
Пример 2. Определите, какие из изображенных на рисунке функций инъективны, а какие сюръективны. Перечислите все биекции. Какие, из функций имеют обратные. Какие функции являются обратимыми?
а) не инъекция, т.к. в области значений 1 соответствует a и b из области определения. Не сюръекция, т.к. элементу 2 из области значений не соответствует ни один элемент из области определения.
б) инъекция, т.к. каждый элемент из области значений переходит в один элемент из области определения. Сюръекция, т.к. множество значений функции совпадает со всей областью значений, т.к. функция инъективна и сюръективна, то она биективна.
в) не инъекция (а, b ® 1). Сюръекция: в множество значений функции входят все элементы области значений.
г) инъекция, но не сюръекция, т.к. заняты не все элементы множества значений.
Среди вышеперечисленных примеров, обратима лишь функция примера (б), т.е. обратимы лишь биекции.
Пример 3. Является ли отношение R = {(1,4), (2,3), (3,2), (4,1)}, заданное на декартовом квадрате множества А= {1, 2, 3, 4}, биективным отображением? 1) отображением является. Т.к. каждый элемент х (из области значений это 1, 2, 3,4) входит в пары вида (x,y) один раз; 2) отображение инъективно, т.к. для различных первых элементов вторые тоже различны; 3) сюръективно, т.к. правая часть отношения R сопадает с множеством A (область значений) 4) т.к. отображение инъективно и сюръективно, то оно биективно.
Пример 4. Пусть А= {0, 2, 4, 6}, B = {1,3, 5, 7}. Какие из нижеперчисленных отношений между множествами A и B являются функциями, определенными на A со значениями в B. а) {(6,3), (2,1), (0,3), (4,5)}; б) {(2,3), (4,7), (0,1), (6,5)}; в) {(2,1), (4,5), (6,3)}; г) (6,1), (0,3), (4,1), (0,7), (2,5)
Какие функции инъективны, какие сюръективны? а) функция не инъективна, т.к. 6 и 0 переходят в один элемент – в "3"Î B, не сюръективна, т.к. элемент "7"Î B не входит в множество её значений; б) f инъективна (каждый образ имеет свой прообраз) и сюръективна в множество значений входят все элементы этого множества; в) не функция, т.к. элементу 0 из множества А не поставлен в соответствии ни один элемент из множества B; г) не функция, т.к. элементу 0 из множества А соответствут 2 элемента: 3,7Î B.
Пример 5. Участниками математической олимпиады предложено 5 задач. Являются ли функцией соответствие, сопоставляющее каждому участнику: а) номера решений задач; б) å № - ов решений задач. а) нет – т.к. некоторым участникам будет сопосталяется несколько номеров б) да, при условии, что участнику олимпиады, не решившему ни одной задачи, сопоставляется число 0. Работу составила преподаватель Т.С. Пронина Практическое занятие № 15 1 Наименование работы: Предикаты. Область определения и область истинности предикатов. Операции над предикатами. 2 Цель работы: Научиться выделять предикаты, находить область определения и область истинности предикатов, выполнять операции над предикатами. Формирование ОК 1, 3, 4-6, 9; овладение знаниями и умениями, необходимыми для освоения ПК 3.4. (спец. 09.02.03.), ПК 1.1, 1.2. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: Предикаты. 4 Литература: 4.1 Конспект лекций по учебной дисциплине «Элементы математической логики», 2016 4.2 Приложение к ПЗ №15. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: Основная часть 6.1 Какие из следующих выражений являются предикатами? Для предикатов определите их местность.
а)
6.2 Какие вхождения переменных являются свободными, а какие связанными в следующих формулах: а)
6.3 На множестве M = {3, 6, 9, 12......... 42} определены предикаты: P(x) - "число Х делится на 6" Q(x) - "число Х Найдите область истинности предиката
6.4 Заданы предикаты:
Запишите следующие высказывания: а) б) в) г) Т (Джон, Сью, Мэри) 6.5 Определите область истинности предиката P (x, y): ((x+y) нечетно Ù (|x-y| £ 1)), где x= {5, 8, 9}, y= {4, 7, 8, 10}.
Вариативная часть 6.6 Рассмотрите зависимость значения истинности предиката от его области определения на примерах:
Укажите такую область определения для каждого предиката, чтобы предикат был истинен.
6.7 Запишите приведенные ниже утверждения в символьной форме с помощью предикатов и кванторов. а) Сумма любых трех последовательностей целых чисел делится на 3. б) Среди трех любых целых чисел, найдутся два, сумма которых четна. Истинно ли это утверждение?
6.8 Запишите в виде высказывания а) ("DABC)($!окр l)(A,B,CÎ б) (" a, b,Î R, a ¹0)($!Î R)(ax = b)
7 Порядок выполнения работы: Выполните практическую работу в соответствии с заданиями (основная часть 6.1 – 6.5) и сдайте зачет. В случае получения зачета, выполните вариативную часть (6.6- 6.8). 8 Содержание отчета: Решения задач в соответствии с заданием. 9 Контрольные вопросы: 1 Что называется предикатом? 2 Может ли предикат стать высказыванием? Если да, то при каких условиях? 3 Приведите примеры одно-, двух-, и трехместного предикатов. 4 Какой предикат называется разрешимым? Тождественно истинным, тождественно ложным? 5 Что обозначают и как читаются кванторы 6 Какая переменная считается свободной, а какая связанной?
Приложение к практическому занятию по ЭМЛ № 15 Рассмотрим пример: «х простое число». Это выражение не является высказываем, но если в нем переменную х заменить на определенное число, то получим высказывание. Причем при замене х на число 3 получим истинное высказывание, тогда как при замене х на 8 получим ложное высказывание. Таким образом, выражение: «х простое число» можно рассматривать как функцию Р(х), зависящую от переменной х. Область определения Р(х) – множество чисел, а область значения – высказывание. Предикаты – функция, значениями которой являются высказывания о n объектах, представляющих значения аргументов. Чтобы задать n – местный предикат Р (х1, х2, …, хn), следует указать множества Х1, Х2, …, Хn – области изменения переменных х1, х2, …, хn, причем чаще всего рассматривается случай, когда Х1 = Х2 = … = Хn. С теоретико-множественной точки зрения предикат определяется заданием подмножества M в декартовом произведении Х1, Х2, …, Хn, которые называются предметными переменными. Элементы множеств Х1, Х2, …, Хn называются предметами. Множество М – множество кортежей длины n < х1, х2, …, хn > называется полем предиката Р (х1, х2, …, хn). Будем обозначать предметные переменные малыми буквами конца латинского алфавита (иногда будем снабжать эти буквы индексами) x, y, z, … х1, х2, …, хn. Предметы их множеств Х1, Х2, …, Хn – малыми буквами начала латинского алфавита a, b, c, …, a1, a2, a3 …. Предикаты – большими буквами латинского алфавита с приписанными предметными переменными или без них A(х), В, F(x, y), Р (х1, …, хn). Число переменных будем указывать как верхний индекс у предиката: Рk (х1, х2, …, хk) – k местный предикат, Q2(х, у) – двуместный предикат, Р(х) – одноместный предикат. Итак, n – местный предикат – Рn (х1, х2, …, хn) есть функция, предметные переменные которой принимают значения из некоторого множества Mk, а сама она принимает только два значения: истина (1) или ложь (0), т.е. предикат - Предикат называется разрешимым (выполнимым), если существуют такие кортежи, компоненты которых обращают предикат в истинное высказывание. Если предикат при подстановке любых конкретных элементов из соответствующих множеств обращается в ложное высказывание, он называется тождественно ложным. Если предикат при подстановке любых конкретн
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 873; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.61.142 (0.26 с.) |

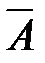 . Это соответствует логической операции отрицания. Диаграмма Эйлера-Венна для дополнения изображена на рис.8, а таблица истинности логической операции высказывания
. Это соответствует логической операции отрицания. Диаграмма Эйлера-Венна для дополнения изображена на рис.8, а таблица истинности логической операции высказывания 
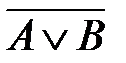 и А|В =
и А|В = 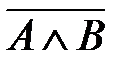 .
.


 . Диаграмма Эйлера-Венна для разности изображена на рис.12, а таблица истинности логической операции высказывания представлена таблицей 6.
. Диаграмма Эйлера-Венна для разности изображена на рис.12, а таблица истинности логической операции высказывания представлена таблицей 6.
 . Поэтому множество для X®Y будет тем же, что и множество истинности для
. Поэтому множество для X®Y будет тем же, что и множество истинности для 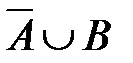 (рис. 13, таблица 7).
(рис. 13, таблица 7).
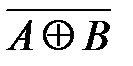 .
.
 и
и 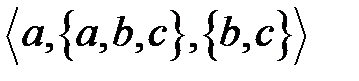 ;
;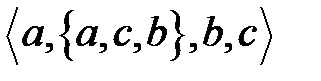 ;
; ;
;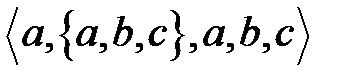 .
. y, x£ 3}.
y, x£ 3}.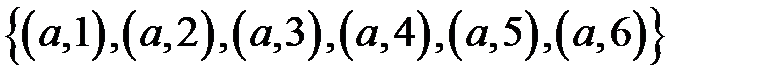 ;
; ;
;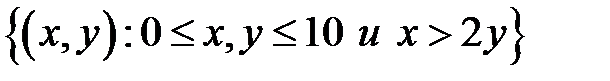 .
.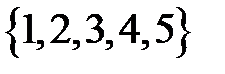 ;
; ;
;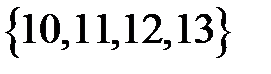 ;
; .
.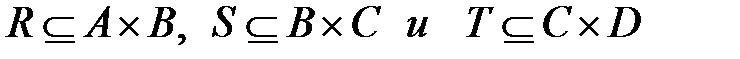 определены следующим образом
определены следующим образом ;
;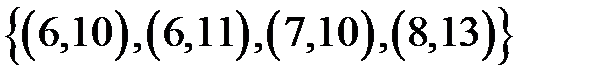 ;
;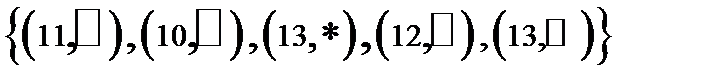 ;
;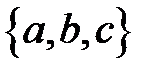 . Задайте рефлексивное отношение, которое не являлось бы симметричным и транзитивным.
. Задайте рефлексивное отношение, которое не являлось бы симметричным и транзитивным. Xk.
Xk.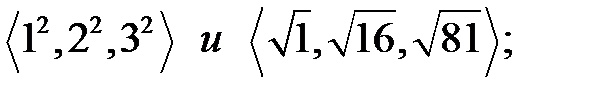 б)
б) 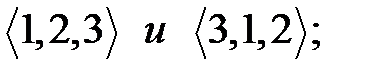 в)
в) 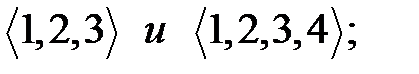
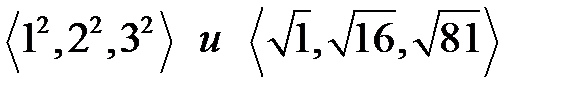 равны, поскольку 12 =
равны, поскольку 12 = 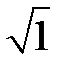 ; 22 =
; 22 = 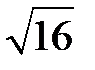 ; 32 =
; 32 =  ;
; различны, хотя имеют одинаковую длину и одно и то же множество координат, но эти координаты располагаются в разном порядке;
различны, хотя имеют одинаковую длину и одно и то же множество координат, но эти координаты располагаются в разном порядке; различны, так как имеют разную длину.
различны, так как имеют разную длину.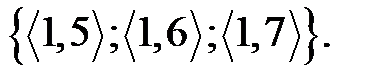
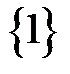 ; PR =
; PR = 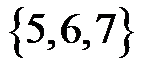 .
.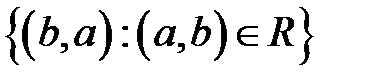 .
.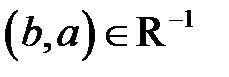 тогда и только тогда, когда
тогда и только тогда, когда  или, что равносильно, bR-1a тогда и только тогда, когда aRb. Отношение R-1 называется обратным отношением к данному отношению R.
или, что равносильно, bR-1a тогда и только тогда, когда aRb. Отношение R-1 называется обратным отношением к данному отношению R.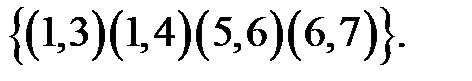 Определите обратное бинарное отношение
Определите обратное бинарное отношение
 существует такой элемент b из B
существует такой элемент b из B 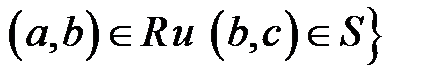 .
.

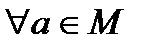
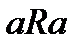 или (при задании бинарных отношений в матричном виде) главная диагональ
или (при задании бинарных отношений в матричном виде) главная диагональ 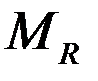 матрицы содержит только единицы. Отношение «быть равным», «меньше или равно» и т.д. является рефлексивным.
матрицы содержит только единицы. Отношение «быть равным», «меньше или равно» и т.д. является рефлексивным.
 или главная диагональ
или главная диагональ 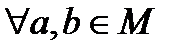
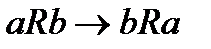 . В матричном виде задания бинарного отношения
. В матричном виде задания бинарного отношения 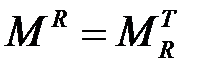 , т.е. матрица отношения симметрична относительно главной диагонали (например, с13= с31; с36= с63 и т.д.
, т.е. матрица отношения симметрична относительно главной диагонали (например, с13= с31; с36= с63 и т.д.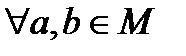
 и
и 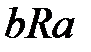 следует
следует 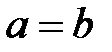 - условие антисиметричности или
- условие антисиметричности или 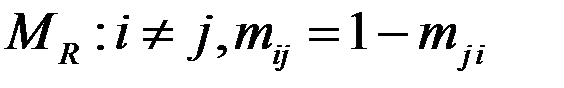 . Если для несовпадающих элементов (
. Если для несовпадающих элементов (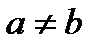 ) верно отношение,
) верно отношение, 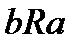 , антисимметрично «быть строго меньше», «строго больше», «быть делителем» на N «быть младше» на множестве людей.
, антисимметрично «быть строго меньше», «строго больше», «быть делителем» на N «быть младше» на множестве людей.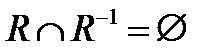 (быть отцом» «быть сыном»)
(быть отцом» «быть сыном»)
 и
и 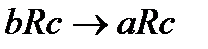 . Для транзитивности отношения R необходимо и достаточно, чтобы
. Для транзитивности отношения R необходимо и достаточно, чтобы 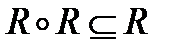 ,
,

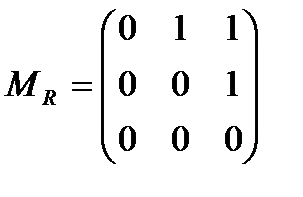

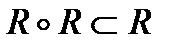 , т.е. R – транзитивно
, т.е. R – транзитивно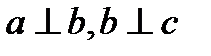 , но неверно, что
, но неверно, что  ).
). . Функция f1 сюръективна, но не инъективна, функция f2 инъективна, но не сюръективна, функция f3 биективна, функция f4 не инъективна и не сюръективна.
. Функция f1 сюръективна, но не инъективна, функция f2 инъективна, но не сюръективна, функция f3 биективна, функция f4 не инъективна и не сюръективна.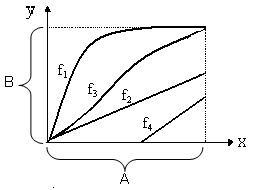
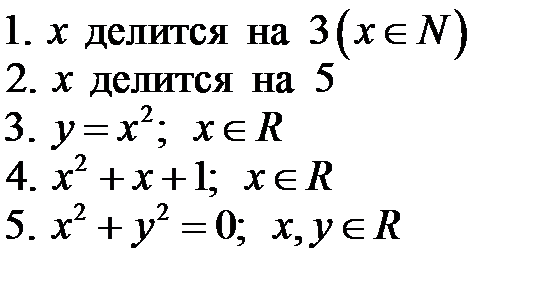

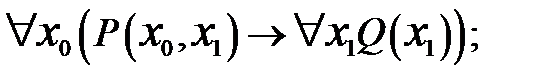 б)
б) 
 30"
30"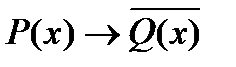

 ;
;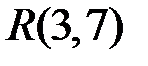 ;
;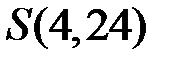 ;
;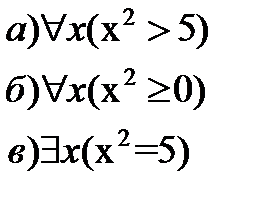
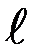 )*
)* ?
?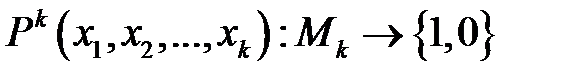 - это связное повествовательное предложение, содержащее n переменных и обладающее следующим свойством: при фиксации значений всех переменных о нем (предложении) можно сказать, истинно оно или ложно.
- это связное повествовательное предложение, содержащее n переменных и обладающее следующим свойством: при фиксации значений всех переменных о нем (предложении) можно сказать, истинно оно или ложно.


