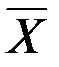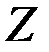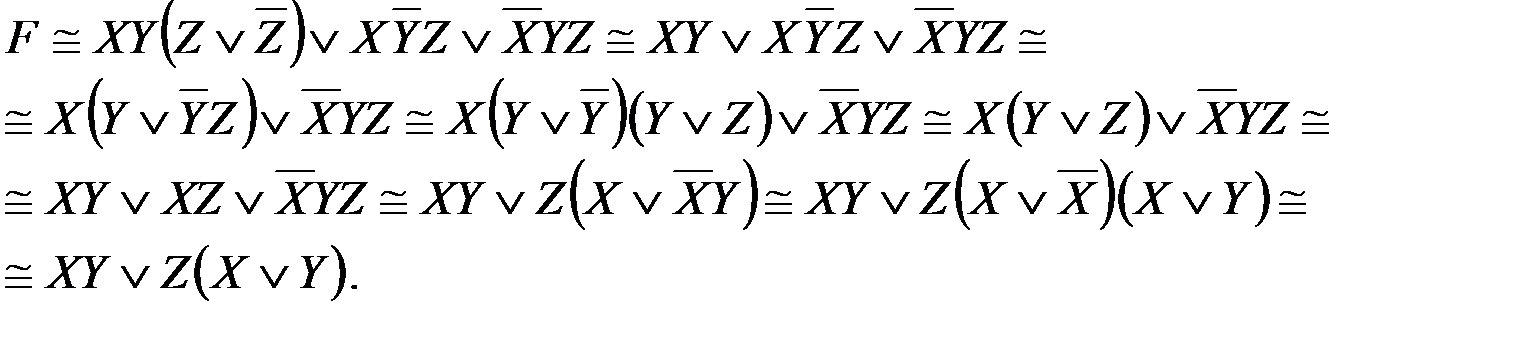Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Совершенные нормальные формы
СДНФ можно определить, используя таблицы истинности. При этом для нахождения СДНФ следует выделить строки со значением f= 1 и выписать все элементарные конъюнкции, а затем соединить их знаками дизъюнкций. При написании элементарных конъюнкций следует включить их с отрицанием, если переменная функции принимает в таблице истинности значение 0 и без отрицания, если переменная функции принимает значение 1. Для построения СКНФ следует в таблице истинности выделить строки, где функция принимает значение 0 и выписать совершенные элементарные дизъюнкции, заключить их в скобки и соединить знаками конъюнкции. При написании совершенных элементарных дизъюнкций следует брать переменные, входящие в совершенную элементарную дизъюнкцию с отрицанием, если переменная функции принимает значение 1 и без отрицания, если переменная принимает значение 0. Формулы, описывающие СДНФ и СКНФ функции, позволяют сформулировать следующие утверждения: 1. Каждая булева функция от n переменных, отличная от константы 0, имеет единственную СДНФ. 2. Каждая булева функция от n переменных, отличная от константы 1, имеет единственную СКНФ. Эти утверждения называются теоремой о функциональной полноте.
Пример 1. Найдите СДНФ и СКНФ функции f (x1, x2, x3), заданной следующей таблицей истинности:
СДНФ имеет вид:
СКНФ имеет вид:
Описанный способ нахождения СДНФ и СКНФ по таблице истинности бывает часто более трудоемким. Второй способ нахождения СДНФ описан ниже. Для нахождения СДНФ данную формулу приводим сначала к ДНФ, а затем преобразовываем ее конъюнкции с помощью следующих действий: а) если в конъюнкцию входит некоторая переменная без отрицания и со своим отрицанием, то мы удаляем эту конъюнкцию из ДНФ; б) если в конъюнкцию одна и та же переменная входит несколько раз, то все они удаляются, кроме одной; в) если в конъюнкцию не входят некоторые переменные, то для каждой из них к конъюнкции добавляется соответствующая формула вида: г) если в полученной ДНФ имеется несколько одинаковых конъюнкций, то оставляем только одну из них.
В результате получается СДНФ.
Пример 2. Найдите СДНФ для ДНФ Решение. 1. Удаляем конъюнкцию 2. Из конъюнкции 3. В первой конъюнкции нет переменных у и z, поэтому к ней добавляется формула
4. Используем дистрибутивные законы:
5. К первой и второй конъюнкциям добавляем
6. Используем дистрибутивные законы:
7. В полученной формуле имеется две одинаковые конъюнкции
В итоге мы получили соответствующую СДНФ. Пример 3. Найдите СКНФ для КНФ ______________ Для упрощения понимания * в прямоугольниках показаны порядковые номера дизъюнкций, которые затем объединятся знаками дизъюнкций. Решение. Алгоритм приведения КНФ к СКНФ аналогичен вышеизложенному приведению ДНФ К СДНФ. 1. Во второй дизъюнкции не хватает переменной y, поэтому в дизъюнкцию добавим
2. В третью дизъюнкцию добавим
3. Объединим все дизъюнкции знаками конъюнкции:
4. Избавляемся от одинаковых дизъюнкций, оставляя только одну. В результате получается СКНФ:
Функция может быть задана не таблицей истинности, а набором переменных, значение функции на котором равно 1. Пример 4. Используя СДНФ, найдите булеву функцию, принимающую значение 1 на следующих наборах переменных, и только на них: f (0, 1, 0) = f (1, 0, 1) = f (1, 1,1) = 1. Решение. Алгоритм построения СДНФ. 1. Наборам 010; 101; 111 соответствуют конъюнкции:
2. Составим дизъюнкцию полученных конъюнкций, т.е. составляем СДНФ функции: f (x1, x2, x3)=
Единичный n -мерный куб Множество двоичных наборов длины n образует n – мерный булев (или двоичный) куб, который называют также единичным n – мерным кубом и обозначают Вn или Наборы
Такой n – мерный куб будет однозначно задавать любую булеву функцию
рис.1
Пример 5. Функция трех переменных задана на единичном трехмерном кубе. Найдите ее СДНФ.
СДНФ будет выглядеть так:
Работу составила преподаватель Т.С. Пронина
Практическое занятие №7 1 Наименование работы: Минимизация нормальных форм. 2 Цель работы: Научиться минимизировать СКНФ и СДНФ с помощью карты Карно и алгебраических преобразований. Формирование ОК 1,2,3; овладение знаниями и умениями, необходимыми для освоения ПК 2.4, 3.4. (спец. 09.02.03.), ПК 1.4, 2.4. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: Минимизация нормальных форм. 4 Литература: 4.1 Конспект лекций по учебной дисциплине «Элементы математической логики», 2016 4.2 Приложение к ПЗ №7. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: Основная часть 6.1 Минимизируйте СДНФ а) б) в) г) 6.2 Определите СДНФ и минимизируйте ее с помощью карты Карно и логических преобразований. Сравните результаты, если f (x,y,z) = 6.3 Минимизируйте СДНФ функций, заданных набором переменных. а) f (0,0,0) = f (0,0,1) = f (1,0,1) = f (1,1,1) =1 б) f (0,0,0) = f (1,1,1) = f (1,1,0) = 0 в) f (1,0,0) = f (0,1,1) = f (0,1,0) = 0 г) f (0,1,1) = f (0,1,0) = f (1,0,1) = f (1,1,1)= 0 д) f (0,1,1) = f (1,0,0) = f (1,0,1) = 1 Вариативная часть 6.4 Найдите СДНФ функции:
6.5 Перейдите от СКНФ к СДНФ, используя закон двойственности, минимизируйте ее:
6.6 Минимизируйте СДНФ функций f1, f2, f3 (см. таблицу 1). 1) методом карт Карно; 2) с помощью логических преобразований.
Таблица 1
7 Порядок выполнения работы: Выполните практическую работу в соответствии с заданиями (основная часть п.п. 6.1 – 6.3) и сдайте зачет. В случае получения зачета, выполните вариативную часть (6.4-6.6). 8 Содержание отчета: Решения задач в соответствии с заданием. 9 Контрольные вопросы:
1 Какими способами можно минимизировать СДНФ, СКНФ? 2 Как минимизировать СДНФ, СКНФ с помощью логических операций? 3 Как минимизировать СДНФ с помощью карты Карно? Приложение к практическому занятию по ЭМЛ № 7 Минимизация нормальных форм с помощью эквивалентных преобразований Под упрощением булевой функции подразумевается эквивалентное выражение, использующее после проведенного преобразования меньше символов, чем исходное. Метод состоит в упрощении дизъюнктивной нормальной формы булевой функции, несмотря на то, что эта форма может оказаться более громоздкой, чем сама функция. Ниже приведены преобразования булевых функций от трех переменных. При желании разработанную технику можно будет обобщить на функции с любым числом аргументов. Пример 1. Минимизировать выражение: Прежде всего, записывая функцию, следует опускать символ аналогично тому, как в обычной алгебре опускают символ умножения. Например, мы будем писать Это выражение – дизъюнктивная нормальная форма. Его можно упростить следующим образом:
= Мы получили выражение, существенно более простое, чем исходная функция. Последовательность шагов, которые мы совершили, упрощая функцию, можно делать почти автоматически. 1) На первом шаге мы сделали перегруппировку: переставили и взяли в скобки два слагаемых, отличающиеся только в одном символе. 2) Закон дистрибутивности позволил на втором шаге вынести одно из слагаемых за скобки, исключив из него булеву переменную y.
Карта Карно Упрощение функций можно делать с помощью карты Карно, метода, изобретенного в 1950-ых годах для разработки логических схем. Карта Карно – эта наглядная схема, предназначенная для обнаружения пар слагаемых, которые можно сгруппировать и преобразовать в одно простое выражение. В случае булевых функций трех переменных x, y и z карта Карно представляет собой таблицу с двумя строками и четырьмя столбцами (рис.1). Столбцы обозначены дизъюнкциями, которые можно получить из двух переменных x и y и их отрицаний, а строки – переменной z и ее отрицанием xy z
рис. 1 Форма карты Карно для функций трех переменных Метки расставлены таким образом, что от столбца к столбцу в них происходит изменение ровно в одном символе. Ячейки карты Карно соответствуют восьми слагаемым, которые можно построить из трех булевых переменных. Если нам дано булево выражение в дизъюнктивной нормальной форме, то в ячейки, соответствующие слагаемым, участвующим в ней, мы записываем цифру 1.
Пример 2. Составить карту Карно для выражения
рис. 2 Карта Карно выражения
Затем предлагается «группировать» пары «соседних единиц» в карте Карно (похожих на ту, которая выделена на рис.2). Такая пара в нашем примере только одна. Она соответствует именно тем слагаемым, которые мы объединили в сделанных ранее алгебраических преобразованиях, т.е. ответ: При этом нужно учитывать, что при сворачивании карты в кольцо пары xyz и
Пример 3. Минимизировать СДНФ:
рис. 3 Карта Карно выражения
Поэтому выражение
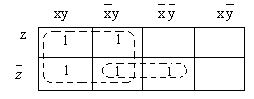
Пример 4. Упростите булево выражение На рис.5 изображена соответствующая карта Карно.
рис. 5 Карта Карно выражения
Из нее следует, что в данном выражении есть группа из четырех слагаемых:
которую мы обозначим через (А), и группа из двух слагаемых: Ее мы обозначим через (Б). Первые два слагаемых в группе А преобразуются в Группа Б преобразуется следующим образом: По карте Карно четырехкратный блок можно описать, используя только одну компоненту, в данном случае y, а двукратный блок – двумя компонентами: Таким образом, исходное выражение упрощается до Внимательно следя за таким преобразованиями, можно заметить, что слагаемое
Пример 5. Построить карту Карно для четырех переменных. Дано выражение:
Размещая единицы в карте Карно, получаем карту, изображенную на рис.6, которую можно покрыть восьмикратным, четырехкратным и двукратным блоками. Восьмикратный блок можно описать, используя только одну из компонент x, y, z, t. В данном случае восьмикратный блок описывает y. Четырехкратный блок можно описать, используя только два простых высказывания. В данном случае этот блок можно описать, используя xÙt. Двукратный блок можно описать, используя три простых высказывания. В данном случае это
рис.6 Карта Карно для четырех переменных
Практическое занятие № 8 1 Наименование работы: Применение булевых функций к релейно- контактным схемам.
2 Цель работы: Научиться производить анализ и синтез релейно- контактных схем. Формирование ОК 1- 5, 8, 9; овладение знаниями и умениями, необходимыми для освоения ПК 2.4, 3.4. (спец. 09.02.03.), ПК 1.4, 2.4. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите темы: Анализ и синтез релейно- контактных схем. 4 Литература: 4.1 Конспект лекций по учебной дисциплине «Элементы математической логики», 2016 4.2 Приложение к ПЗ №8. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: Основная часть 6.1 Постройте РКС с заданной функцией проводимости 1) 2) 3) 4)
6.2 Найдите функции проводимости следующих схем, если возможно, упростите схемы.
 2) 2)
3)
6.3 Постройте наиболее простую РКС с тремя переключателями а) переключатель б) переключатель в) только два переключателя разомкнуты. Вариативная часть: 6.4 Постройте РКС с заданной функцией проводимости 1. 2.
6.5 Найдите функции проводимости следующих схем, если возможно, упростите схемы. 1.
2.
6.6 Комитет из 4 человек принимает решение в случае, когда не менее трех человек, один из которых председатель проголосовали «за». Построить схему так, чтобы голосование проходило нажатием кнопок и, в случае принятия решения, загоралась лампочка.
7 Порядок выполнения работы: Выполните практическую работу в соответствии с заданиями (основная часть 6.1 – 6.3) и сдайте зачет. В случае получения зачета, выполните вариативную часть (6.4- 6.6). 8 Содержание отчета: Решения задач в соответствии с заданием. 9 Контрольные вопросы: 1 Что называется релейно- контактной схемой? 2 Как на чертежах изображаются все замыкающие и размыкающие контакты, подключенные к переключателю? 3 Какие две РКС называются равносильными? 4 Каждой ли РКС можно поставить в соответствие булеву функцию, и наоборот? 5 Какие две основные задачи выделяют в теории РКС?
Приложение к практическому занятию по ЭМЛ № 8 Под релейно-контактной схемой понимают устройство из проводников и двухпозиционных контактов, через которые полюсы источника тока связаны с некоторым потребителем. Контакты могут быть замыкающие или размыкающие. Каждый контакт подключен к некоторому переключателю (реле). Когда переключатель находится в рабочем состоянии, все подключенные к нему замыкающие контакты замкнуты, размыкающие контакты разомкнуты, в противном случае наоборот. Каждому переключателю ставится в соответствие булева переменная, которая принимает значение 1, если переключатель находится в рабочем состоянии, и 0 в противном случае. На чертежах все замыкающие контакты, подключенные к переключателю
а размыкающие изображаются
Всей РКС ставится в соответствие булева функция от переменных Две РКС называются равносильными, если одна из них проводит ток тогда и только тогда, когда другая схема проводит ток. Из двух равносильных схем более простой считается та, которая содержит меньшее число контактов.
Рис.1 Рис. 2 Рис. 3
Первая схема состоит из двух последовательно соединенных контактов Вторая схема состоит из двух параллельно соединенных контактов Третья схема, состоящая из размыкающего контакта, проводит ток тогда и только тогда, когда переменная Любая булева функция может быть представлена в виде формулы алгебры высказываний, которая может быть записана в КНФ или в ДНФ. Следовательно, каждой булевой функции можно поставить в соответствие некоторую РКС, и, наоборот, каждой РКС можно поставить в соответствие некоторую булеву функцию или формулу алгебры высказываний. Поэтому возможности схемы можно выяснить, изучая соответствующую ей формулу, а упрощение схемы можно свести к упрощению формулы. Выделяют следующие основные задачи теории релейно-контактных схем. 1. Задачи синтеза. Эта задача состоит в построении РКС с заданными условиями работы. Для этого по заданным условия составляется таблица значений функции проводимости 2. Задача анализа схем. Эта задача состоит в нахождении функции проводимости данной схемы, анализе этой функции, построении более простой схемы, имеющей такую же функцию проводимости. Решение задач синтеза и анализа РКС продемонстрируем на примере. Пример 1. Постройте наиболее простую РКС с тремя переключателями Используя условие, составим таблицу значений функции проводимости этой схемы.
По таблице составим СДНФ для функции
Построим схему для функции
Упростим построенную РКС с помощью равносильных преобразований формулы
Тогда упрощенная схема выглядит так.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 973; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.72.78 (0.209 с.) |
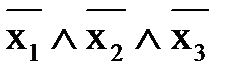
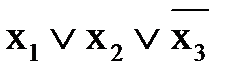
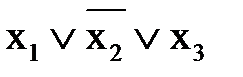


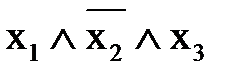
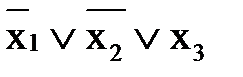
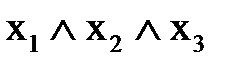


 ;
;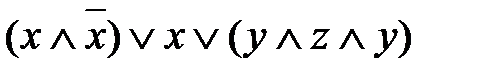 .
.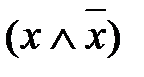 , так как здесь переменная вместе со своим отрицанием. Остается
, так как здесь переменная вместе со своим отрицанием. Остается  .
. удаляем переменную y, так как она входит сюда два раза. Остается
удаляем переменную y, так как она входит сюда два раза. Остается  .
.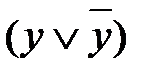 , а также
, а также  , а во второй конъюнкции нет переменной x, поэтому к ней добавляется формула
, а во второй конъюнкции нет переменной x, поэтому к ней добавляется формула  , действия производим поэтапно. Получаем:
, действия производим поэтапно. Получаем: .
.
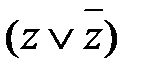 и получаем:
и получаем: .
.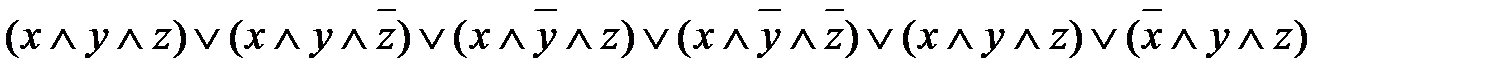
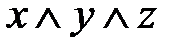 . Удалив одну из них, получим:
. Удалив одну из них, получим: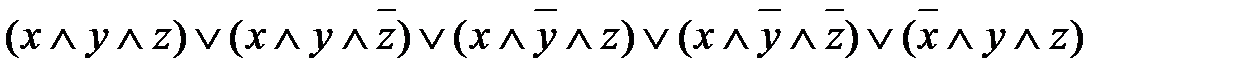 .
.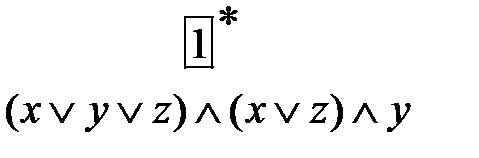 .
.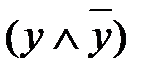 и, используя дистрибутивные законы, получаем:
и, используя дистрибутивные законы, получаем: 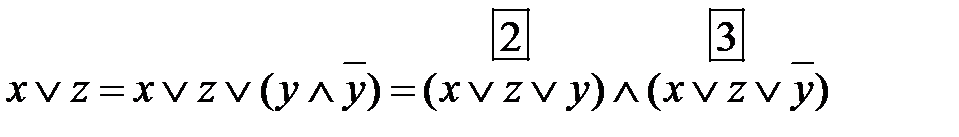 .
. и получим две дизъюнкции:
и получим две дизъюнкции: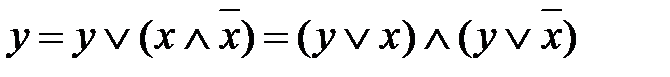 . Добавив в каждую из них
. Добавив в каждую из них 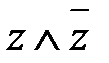 , получим:
, получим: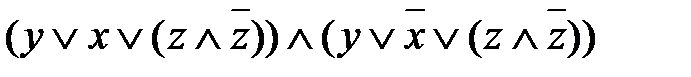 =
= 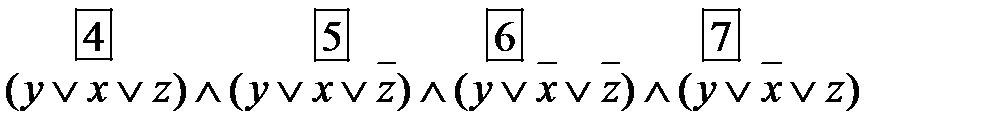 .
.
 .
.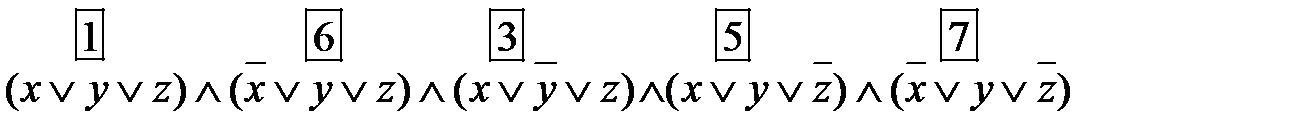 .
.
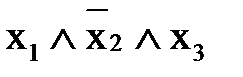

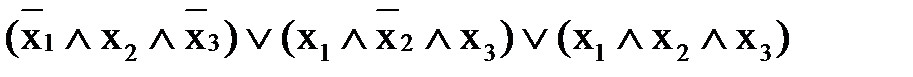 .
.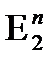 .
.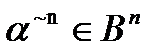 называют вершинами куба Вn . Каждой вершине n – мерного единичного куба можно приписать конкретное значение 0 или 1, которое принимает булева функция при соответствующем наборе аргументов (векторов
называют вершинами куба Вn . Каждой вершине n – мерного единичного куба можно приписать конкретное значение 0 или 1, которое принимает булева функция при соответствующем наборе аргументов (векторов 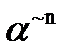 ). Если значение функции равно 0, то точка не рисуется (выкалывается). Если же значение функции равно 1, то точка рисуется – выделяется полужирно.
). Если значение функции равно 0, то точка не рисуется (выкалывается). Если же значение функции равно 1, то точка рисуется – выделяется полужирно.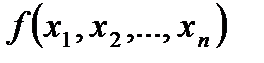 . Например, для двух переменных геометрическая интерпретация булевой функции будет на плоскости иметь вид квадрата или «двумерного куба» (рис. 1), а для трех переменных – трехмерного куба – куба в пространстве (рис. 2).
. Например, для двух переменных геометрическая интерпретация булевой функции будет на плоскости иметь вид квадрата или «двумерного куба» (рис. 1), а для трех переменных – трехмерного куба – куба в пространстве (рис. 2).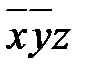
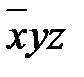
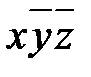
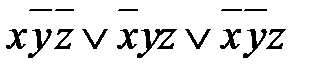 .
.
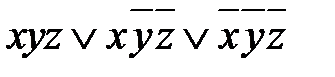
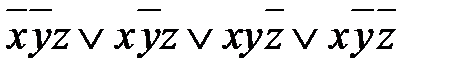
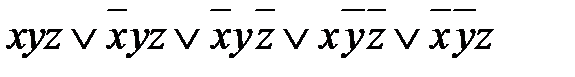
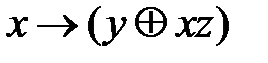
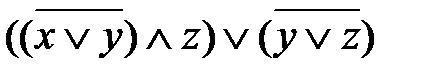 , минимизируйте её.
, минимизируйте её.
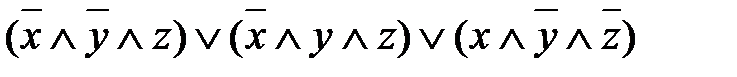
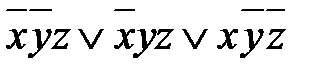 вместо
вместо  = по законам коммутативности и ассоциативности;
= по законам коммутативности и ассоциативности;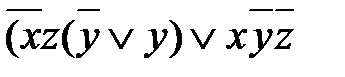 =
= 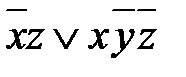 - по закону дистрибутивности, так как
- по закону дистрибутивности, так как 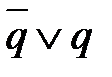 = 1.
= 1.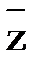 .
.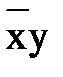
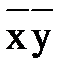
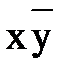
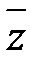
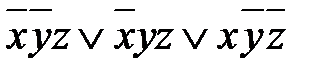 и минимизировать его (рис. 2).
и минимизировать его (рис. 2).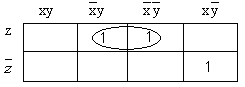
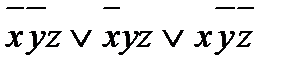
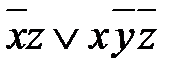 .
.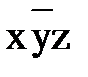 окажутся соседними и их тоже можно группировать.
окажутся соседними и их тоже можно группировать.


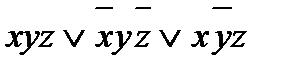 =
= 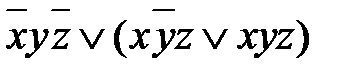 =
= 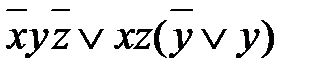 =
=  .
.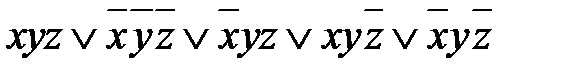

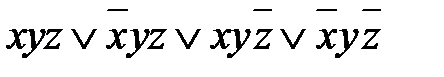 ,
,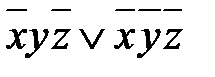
 ). Аналогично, но вторые два слагаемых в группе А преобразуются в
). Аналогично, но вторые два слагаемых в группе А преобразуются в  . Т.о.
. Т.о. 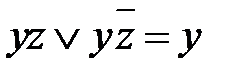 .
.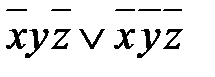 =
= 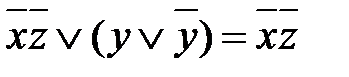 .
.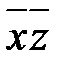 .
.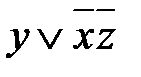 .
.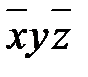 здесь используется дважды, хотя в исходном выражении оно задействовано только один раз. Тем не менее, ошибки никакой нет. Это связано с законом идемпотентности: f = f Ú f, где f – произвольная булева функция.
здесь используется дважды, хотя в исходном выражении оно задействовано только один раз. Тем не менее, ошибки никакой нет. Это связано с законом идемпотентности: f = f Ú f, где f – произвольная булева функция.
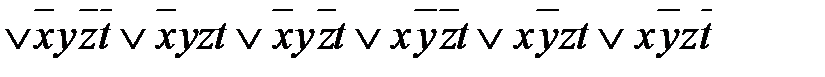
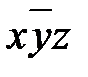 . Следовательно, исходное выражение можно упростить и привести к виду yÚxt Ú
. Следовательно, исходное выражение можно упростить и привести к виду yÚxt Ú 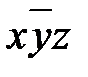 . Поскольку z находится на обоих концах строки, а t находится на обоих концах столбца, «скручивание» карты Карно объединяет эти случаи, так что верхний край можно считать прилегающим к нижнему, а левый – прилегающим к правому.
. Поскольку z находится на обоих концах строки, а t находится на обоих концах столбца, «скручивание» карты Карно объединяет эти случаи, так что верхний край можно считать прилегающим к нижнему, а левый – прилегающим к правому.
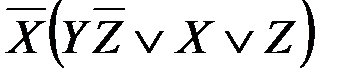



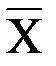
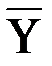
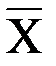


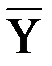
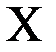
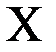
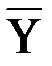


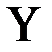



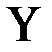
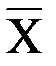
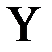
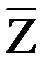
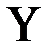
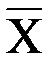
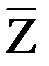
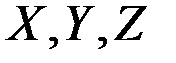 , которая проводит ток тогда и только тогда, когда выполняются по меньшей мере одно из следующих условий:
, которая проводит ток тогда и только тогда, когда выполняются по меньшей мере одно из следующих условий: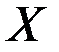 замкнут и только один из оставшихся переключателей замкнут;
замкнут и только один из оставшихся переключателей замкнут;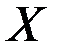 разомкнут, а хотя бы один из оставшихся переключателей замкнут;
разомкнут, а хотя бы один из оставшихся переключателей замкнут;
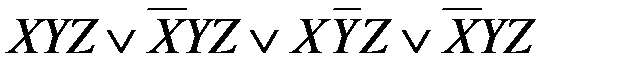

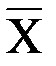
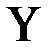

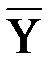
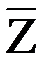
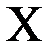




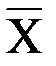
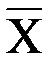
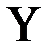
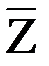
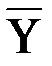

 , изображаются
, изображаются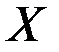
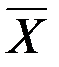

 соответствующих переключателей. Эта функция равна 1, если схема проводит ток, и 0 в противном случае и называется функцией проводимости схемы.
соответствующих переключателей. Эта функция равна 1, если схема проводит ток, и 0 в противном случае и называется функцией проводимости схемы.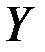
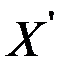
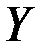
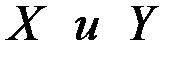 , которая проводит ток тогда и только тогда, когда оба контакта
, которая проводит ток тогда и только тогда, когда оба контакта  .
.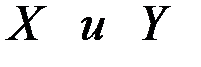 , которая проводит ток тогда и только тогда, когда хотя бы один из контактов
, которая проводит ток тогда и только тогда, когда хотя бы один из контактов 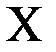 или
или 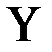 замкнут, то есть тогда и только тогда, когда хотя бы одна из переменных
замкнут, то есть тогда и только тогда, когда хотя бы одна из переменных  или
или  принимает значение 1. Булева функция от двух аргументов, удовлетворяющая такому условию есть дизъюнкция
принимает значение 1. Булева функция от двух аргументов, удовлетворяющая такому условию есть дизъюнкция 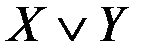 .
.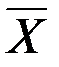 .
.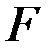 . По таблице составляется СДНФ и СКНФ функции
. По таблице составляется СДНФ и СКНФ функции 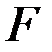 . СДНФ или СКНФ реализуются РКС.
. СДНФ или СКНФ реализуются РКС.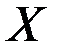

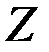


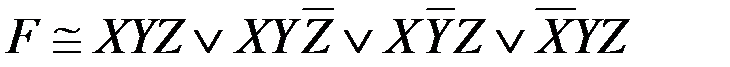 .
.