
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм построения многочлена Жегалкина через сднфСодержание книги
Поиск на нашем сайте
Как известно, любую функцию, отличную от константы 0, можно представить в виде СДНФ. Если сравним таблицы истинности дизъюнкции и суммы по модулю два, видим, что они отличаются только последней строкой, т.е. на наборе 11. Так как в СДНФ на каждом наборе только одна конъюнкция равна 1, то все дизъюнкции можно заменить суммами по модулю два. Кроме того, известно, что 1. Находим множество тех двоичных наборов, на которых функция принимает значение 1. 2. Составляем СДНФ. 3. В СДНФ каждый знак дизъюнкции меняем на знак суммы Жегалкина. 4. Упрощаем, если можно, полученное выражение, используя тождество
5. В полученной формуле каждое отрицание 6. Раскрываем скобки в полученной формуле, содержащей только функции «Ù» и «Å» и константу1. 7. Приводим подобные члены, используя тождество xiÅxi=0.
Пример 1. f (x1, x2, x3) = СДНФ функции = f (x1, x2, x3)= Построим многочлен Жегалкина с помощью СДНФ: выписываем СДНФ функции заменяем знак дизъюнкции на знак суммы Жегалкина Å вынесем из 1 и 2 конъюнкции Проделаем замены
Алгоритм перехода к полиному Жегалкина методом логических преобразований Метод, базирующийся на преобразовании формул над множеством связок {Ù, Пример 2. x®y =
Алгоритм нахождения многочлена Жегалкина методом неопределенных коэффициентов Составляем систему линейных уравнений относительно неизвестных коэффициентов, решением которой являются коэффициенты многочлена Жегалкина. Число уравнений – 2n, где n – число неизвестных Пример 3. Пусть f = xÚy. Запишем полином Жегалкина P(x,y) в общем виде P(x,y) = α0 Å α1х Å α2y Å α3xy. Придавая возможные значения, выписываем систему уравнений для коэффициентов: f (0,0) = 0 = α0 Å α1 ×0 Å α2×0 Å α3×0, отсюда α0 = 0
f (0,1) = 1 = α0 Å α1 ×0 Å α2×1 Å α3×0, отсюда α2 = 1 f (1,0) = 1 = α0 Å α1 ×1 Å α2×0 Å α3×0, отсюда α1 = 1 f (1,1) = 1 = α0 Å α1 ×1 Å α2×1 Å α3×1, отсюда α3 = 1 Т.е. решая эту систему, получаем: α0 =0, α1= α2= α3=1. Следовательно, xÚy = xÅyÅxy. Для проверки составим таблицы истинности левой и правой части равенства.
Таблица истинности
Вывод: преобразование выполнено верно. Линейные функции Функция, у которой полином Жегалкина имеет вид ai, gÎ{0,1}, называется линейной. Иными словами, многочлен Жегалкина называется нелинейным, если он содержит конъюнкции переменных, а если он не содержит конъюнкции переменных, то он называется линейным. Класс линейных функций обозначается Ln (L). Из определения вытекает, что |Ln|= 2n+1. В частности, xÅyÎ L, 0ÎL, xy
Пример 4. Функция f =1001011010010110 = x2Å x3Å x4Å1 линейна.
Работу составила преподаватель Т.С. Пронина
Практическое занятие №10 1 Наименование работы: Операции над множествами. 2 Цель работы: Научиться выполнять операции над множествами. Формирование ОК 2- 5; овладение знаниями и умениями, необходимыми для освоения ПК 1.2. (спец. 09.02.03.), ПК 1.1, 1.2, 2.4. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: Операции над множествами. 4 Литература: 4.1 Конспект лекций по учебной дисциплине «Элементы математической логики», 2016 4.2 Приложение к ПЗ №10. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: Основная часть 6.1 Опишите множества, заданные ниже: а) {0,1,2,…,10} – {xÎZ: x= k, 0£ k £10 } б) {1,4,9,16,25} – {xÎN: x= k2, 1£ k £5 } в) {1,2,3,4,6,12} – {xÎN: 12:x }
6.2 Заданы множества: U = {1,2,3,4,5,6,7} А = {1,2,3,4} В = {3,4,5,6} С = {4,6,7} Выполните операции:
6.3 Заданы множества: A= {1,2,3,4,5,6,7} B= {3,4,5,6,7,8,9} C= {-3,-2,-1,0,1,2,3,4}
D= {2,3,4,5,6} Выполните операции:
6.4 Заданы два множества А = {1, 2, 3}, B = {a, b, c}. Определите декартово произведение AxB. Вариативная часть 6.5 Перечислите элементы множества {x: x- целое и x2 < 100}.
6.6 Опишите множества {Вологда, Владимир, Волгоград, Волгодонск} при помощи характеристического свойства.
6.7 Перечислите подмножества множества {а}.
6.8 Установите истинность или ложность каждого из следующих высказываний: а) Æ Í Æ; б) Æ Ì Æ; в) Æ Î Æ; г) Æ Í А, где А- произвольное множество; д) Æ Î А, где А- произвольное множество.
6.9 Определите количество элементов в каждом множестве: а) {Æ, {Æ}}; б) {{Æ, {Æ}}}; в) {1, 2, 3,{1, 2, 3}}; г) {Æ, {Æ}, a, b,{a, b},{a, b{a, b}}}; д) {Æ, {Æ}, {Æ, {Æ}}}. 7 Порядок выполнения работы: Выполните практическую работу в соответствии с заданиями (основная часть 6.1 – 6.4) и сдайте зачет. В случае получения зачета, выполните вариативную часть (6.5 – 6.9). 8 Содержание отчета: Решения задач в соответствии с заданием. 9 Контрольные вопросы: 1 Что такое множество, подмножество? 2 Что такое булеан? 3 Что такое пустое множество? 4 Как выполнить операции: объединение, пересечение, разность для двух множеств, дополнение множества А, симметрическая разность? Приложение к практическому занятию по ЭМЛ № 10 Множество – это совокупность объектов, называемых элементами множества. Например, {Саратов, Владимир, Тверь}; {2, 3, 5, 7, 11}; {cыр, яйцо, молоко, сметана}. В этом примере элементы каждого множества заключены в фигурные скобки. Чтобы обеспечить возможность ссылок будем обозначать множества латинскими буквами. Например А= {3, 2, 11, 5, 7} – множество, содержащее данные элементы. Заметим, что множество А совпадает с одним из множеств, выписанных выше, поскольку порядок, в котором записываются элементы множества, значения не имеет. В общем случае запись а Î А означает, что объект а – элемент множества А. Часто говорят, что элемент а принадлежит множеству А. Если объект а не принадлежит множеству А, то пишется аÏА. Мы не можем выписать все элементы очень больших, в особенности бесконечных множеств. В этом случае множества определяются с помощью подходящих предикатов. Формально мы пишем: А= {x:P(x)} для описания множества, состоящего из элементов x, для которых предикат P(x) имеет истинное значение. Например, запись A= {x: x – нечетное натуральное число} описывает множество A= {1, 3, 5, 7, …}. Поскольку любое натуральное нечетное число может быть записано в виде 2n-1, где n- любое натуральное число, альтернативное допустимое определение того же множества задается формулой: А= {2n-1: n – натуральное число}.
Пример 1. Найдите более простое описание множеств, перечисляющие их элементы. а) A= {x: x – целое и x2 +4x =12}; б) B= {x: x - название дня недели, не содержащее буквы "е"}; в) C= {n2: n – целое}. Решение. а) Если x2 +4x =12, то x(x+4) = 12. Поскольку x – целое число, делящее 12, то оно может быть равно только ±1, ±2, ±3, ±4, ±6 и ±12. С другой стороны, x+4 тоже делит 12. Поэтому остается только два значения: x= -6 или x=2. Другой способ решения заключается в отыскании корней квадратного уравнения x2 +4x-12 =0. Он приводит к тому же ответу x= -6 или x=2. Следовательно, А= {-6, 2}. б) B= {вторник, пятница, суббота}. в) С= {0, 1, 4, 9, 16,...}.
Некоторые множества чисел столь часто используются, что имеют стандартные названия и обозначения.
N= {1, 2, 3, …} – множество натуральных чисел; Z= {0, ±1, ±2, ±3, …} – множество целых чисел; Q= {p/q: p, q ÎZ, q¹0} – множество рациональных чисел; R= {все десятичные дроби} – множество вещественных чисел. В некоторых книгах натуральные числа включают и 0. Существует несколько способов конструирования нового множества из 2 данных. Опишем коротко эти операции на множествах. Прежде всего отметим, что в вышеприведенных примерах все элементы некоторых множеств принадлежали другим большим множествам. Например, все элементы множества С= {0, 1, 4, 9, 16,…} содержатся в множестве Z= {0, ±1, ±2, ±3,…}. Говорят, что множество С является подмножеством множества Z, если каждый элемент множества С автоматически является элементом множества Z. Довольно часто при этом говорят, что множество C содержится в множестве Z. Этот факт обозначают как C Ì Z. Два множества считаются равными, если каждое из них содержится в другом.
Пример 2. Пусть A= {n: n2 – нечетное целое число}; B= {n: n – нечетное целое число}. Показать, что A=B. Решение. Если xÎA, то x2 – нечетное целое число. Само число x - целое и нечетное. Следовательно, xÎB, т.е. А Ì В. В обратную сторону, пусть xÎB. Тогда x - нечетное целое число. В этом случае x2 тоже будет нечетным целым числом, а значит, xÎА. В виду произвольности взятого элемента xÎB мы можем утверждать, что все элементы из В принадлежат А т.е. В Ì А. Итак, А=В. Объединением двух множеств А и В называется множество АÈВ={x: xÎА или xÎB}. Оно состоит из тех элементов, которые принадлежат либо множеству А, либо множеству В, а возможно и обоим сразу. Пересечением двух множеств А и В называется множество АÇВ= {x: xÎA и xÎB}. Оно состоит из элементов, которые принадлежат как множеству А, так и множеству В. Дополнением множества В до множества А называется А\В= {x: xÎA и xÏВ}. Дополнение А\В состоит из всех элементов множества А, которые не принад-лежат В. Если мы оперируем подмножествами некоего большого множества U, мы называем U универсальным множеством для данной задачи. Для подмножества А универсального множества U можно рассматривать дополнение А до U, т.е. U\А. Поскольку в каждой конкретной задаче универсаль-ное множество фиксировано, множество U\А обычно обозначают
Симметрической разностью двух множеств А и В называют множество А∆В= {x: (xÎA и xÏB) или (xÎB и xÏA) }. Оно состоит из всех тех и только тех элементов универсального множества, которые либо принадлежат А и не принадлежат В, либо наоборот, принадлежат В, но не А. Грубо говоря, симметрическая разность состоит из элементов, лежащих либо в А, либо в В, но не одновременно.
Пример 3. Пусть A= {1, 3, 5, 7}; B= {2, 4, 6, 8}; C= {1, 2, 3, 4, 5}. Найдите АÈС, ВÇС, А\С и В∆С. Решение. АÈС= {1, 3, 5, 7, 2, 4}; ВÇС= {2, 4}; А\С= {7}; В∆С= (В\С) È (С\В)= {6, 8} È {1, 3, 5}= {6, 8, 1, 3, 5}.
Пример 4. Пусть А= {x: 1£ x £12 и x четное целое число}; B= {x: 1£ x £12 и x целое число, кратное 3}. Убедитесь, что Решение. Прежде всего заметим, что универсальным множеством здесь служит U= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. Кроме того, А= {2, 4, 6, 8, 10, 12}и В={3, 6, 9, 12}. Поэтому
и
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 1038; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.101.22 (0.013 с.) |

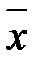 = xÅ1. На этом и основан первый алгоритм построения многочлена Жегалкина:
= xÅ1. На этом и основан первый алгоритм построения многочлена Жегалкина: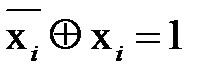 .
.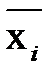 заменяем на xi Å1.
заменяем на xi Å1.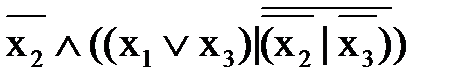 ;
;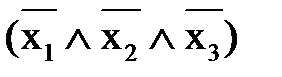 Ú
Ú 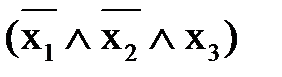 Ú
Ú 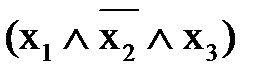
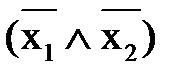 :
: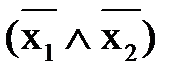 Ù
Ù 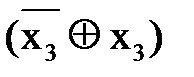 Å
Å  =
= 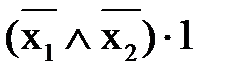 Å
Å 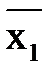 = x1Å1;
= x1Å1; 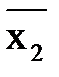 = x2Å1, получаем:
= x2Å1, получаем: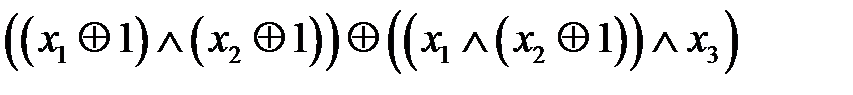 =
= 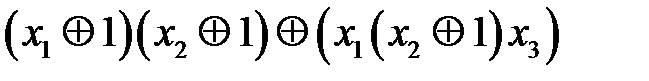 =
=  =
= 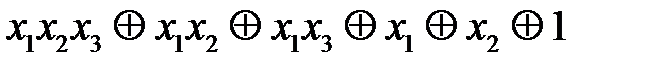 .
. }. Строят некоторую формулу над множеством связок {Ù,
}. Строят некоторую формулу над множеством связок {Ù, 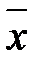 на xÅ1, раскрывают скобки, пользуясь дистрибутивным законом x(yÅz) = xyÅxz, и применяют эквивалентности xx=x, x×1=x, xÅx =0, xÅ0 =x.
на xÅ1, раскрывают скобки, пользуясь дистрибутивным законом x(yÅz) = xyÅxz, и применяют эквивалентности xx=x, x×1=x, xÅx =0, xÅ0 =x.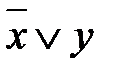 =
= 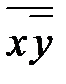 = x (yÅ1) Å1= xy Å x Å1.
= x (yÅ1) Å1= xy Å x Å1.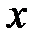
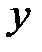
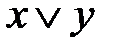
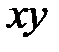
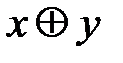
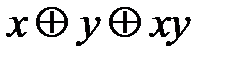
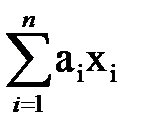 Å g, где
Å g, где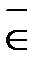 L. Все функции от одной переменной линейны. Линейными функциями от двух переменных являются xÅy и x«y
L. Все функции от одной переменной линейны. Линейными функциями от двух переменных являются xÅy и x«y 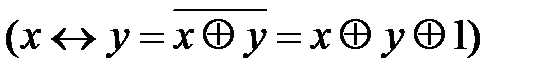 .
.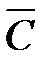 )\B
)\B
 - пустое множество;
- пустое множество;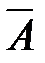 и называют просто дополнением множества А. Таким образом, понимая, что мы работаем с подмножествами универсального множества U, можно записать
и называют просто дополнением множества А. Таким образом, понимая, что мы работаем с подмножествами универсального множества U, можно записать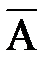 = {x: не (xÎА)}Û
= {x: не (xÎА)}Û 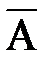 = {x: xÏA}.
= {x: xÏA}.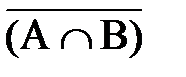 =
= 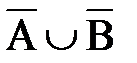
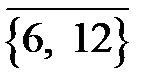 = {1, 2, 3, 4, 5, 7, 8, 9, 10, 11}
= {1, 2, 3, 4, 5, 7, 8, 9, 10, 11}


