
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Термодинамические процессы идеальных газовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
в закрытых системах
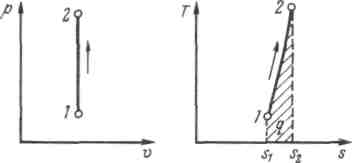
Основными процессами, весьма важными и в теоретическом, и в прикладном отношениях, являются: изохорный, протекающий при постоянном объеме; изобарный, протекающий при постоянном давлении; изотермический, происходящий при постоянной температуре; адиабатный — процесс, при котором отсутствует теплообмен с окружающей средой, и политропный, удовлетворяющий уравнению Опыт показывает, что отдельные процессы, происходящие в тепловых машинах, нередко полностью или частично с достаточной точностью описываются уравнением вида pvn=const, где n - постоянная величина, которая может принимать значения от +∞ до -∞. Метод исследования процессов, не зависящий от их особенностей и являющийся общим, состоит в следующем: выводится уравнение процесса, устанавливающее связь между начальными и конечными параметрами рабочего тела в данном процессе; вычисляется работа изменения объема газа; определяется количество теплоты, подведенной (или отведенной) к газу в процессе; определяется изменение внутренней энергии системы в процессе; определяется изменение энтропии системы в процессе. Изохорный процесс. При изохорном процессе выполняется условие dv = 0 или v = const. Из уравнения состояния идеального газа следует, что p/T=R/v=const, т. е. давление газа прямо пропорционально его абсолютной температуре: Работа расширения в этом процессе равна нулю, так как dv= 0. Количество теплоты, подведенной к рабочему телу в процессе 1-2 при
Рис.2.1.5. Изображение изохорного процесса в р,v- и T, s-координатах
При переменной теплоемкости
где Так как l = 0, то в соответствии с первым законом термодинамики (первый закон имеет вид -
Поскольку внутренняя энергия идеального газа является функцией только его температуры, то полученные формулы справедливы для любого термодинамического процесса идеального газа. Изменение энтропии в изохорном процессе определяется по формуле
т.е. зависимость энтропии от температуры на изохоре при сv=const имеет логарифмический характер. Изобарный процесс. Из уравнения состояния идеального газа при р=const находим
Рис.2.1.6. Изображение изобарного процесса в p,v- и T,s-координатах
Из выражения Так как
Количество теплоты, сообщаемое газу при нагревании (или отдаваемое им при охлаждении):
где Изменение энтропии при ср = const согласно равно
т.е. температурная зависимость энтропии при изобарном процессе тоже имеет логарифмический характер, но поскольку ср>сv, то изобара в Т,s-диаграмме идет более полого, чем изохора. Изотермический процесс. При изотермическом процессе температура постоянна, следовательно, pv = RT = const, или
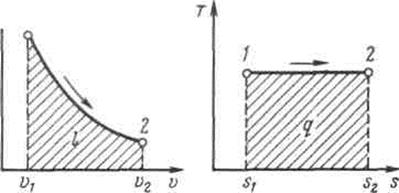
т.е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении — падает (закон Бойля - Мариотта, 1662 г.). Графиком изотермического процесса в р,v – координатах является равнобокая гипербола, для которой координатные оси служат асимптотами (рис.2.1.7). Работа процесса:
Так как температура не меняется, то внутренняя энергия идеального газа в данном процессе остается постоянной (
Рис.2.1.7. Изображение изотермического процесса в р, v- и T, s-координатах
При изотермическом сжатии от газа отводится теплота в количестве, равном затраченной на сжатие работе. Изменение энтропии в изотермическом процессе выражается формулой
Адиабатный процесс. Процесс, происходящий без теплообмена с окружающей средой, называется адиабатным, т.е. Уравнения первого закона термодинамика для адиабатного процесса принимают вид:
Интегрируя последнее уравнение при условии, что k =cp/cv=const, находим
После потенцирования имеем Это и есть уравнения адиабаты идеального газа при постоянном отношении теплоемкостей (k = const). Величина Подставив cp = cv-R, получим k. Согласно классической кинетической теории теплоемкость газов не зависит от температуры, поэтому можно считать, что величина k также не зависит от температуры и определяется числом степеней свободы молекулы. Для одноатомного газа k=1,66 для двухатомного k=1,4, для трех- и многоатомных газов k=l,33. Поскольку k>1, то в координатах р,v линия адиабаты идет круче линии изотермы: при адиабатном расширении давление понижается быстрее, чем при изотермическом, так как в процессе расширения уменьшается температура газа (рис.2.1.8).
Рис.2.1.8. Изображение адиабатного процесса в р, v- и Т, s-координатах
Определив из уравнения состояния, написанного для состояний 1 и 2, отношение объемов или давлений, получим уравнение адиабатного процесса в форме, выражающей зависимость температуры от объема или давления:
Работа расширения при адиабатном процессе согласно первому закону термодинамики совершается за счет уменьшения внутренней энергии и может быть вычислена по одной из следующих формул:
Так как
В данном процессе теплообмен газа с окружающей средой исключается, поэтому q=0. Выражение Поскольку при адиабатном процессе Политропный процесс и его обобщающее значение. Любой произвольный процесс можно описать в р,v - координатах (по крайней мере на небольшом участке) уравнением
подбирая соответствующее значение n. Процесс, описываемый таким уравнением, называется политропным. Показатель политропы n может принимать любое численное значение в пределах от Из уравнения Клапейрона нетрудно получить выражения, устанавливающие связь между р, v и Т в любых двух точках на политропе, аналогично тому, как это было сделано для адиабаты:
Работа расширения газа в политропном процессе имеет вид Так как для политропы в соответствии с (2.1.8)
то
Уравнение (2.1.9) можно преобразовать к виду:
Количество подведенной (или отведенной) в процессе теплоты можно определить с помощью уравнения первого закона термодинамики: Поскольку
где
представляет собой теплоемкость идеального газа в политропном процессе. При постоянных cv, k и n теплоемкость сn = const, поэтому политропный процесс иногда определяют как процесс с постоянной теплоемкостью. Изменение энтропии
Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов. В табл. 2.1.3 приведены характеристики термодинамических процессов. На рис.2.1.9 показано взаимное расположение на р, V- и Т, s-диаграммах политропных процессов с разными значениями показателя политропы. Все процессы начинаются в одной точке («в центре»).
Изохора (n= ± Таблица 2.1.3 Характеристики термодинамических процессов
Рис. 2.1.9. Изображение основных термодинамических процессов идеального газа в р, v- и Т, s-координатах
Процессы, расположенные правее и выше адиабаты, идут с подводом теплоты к рабочему телу; процессы, лежащие левее и ниже адиабаты, протекают с отводом теплоты. Для процессов, расположенных над изотермой (n = 1), характерно увеличение внутренней энергии газа; процессы, расположенные под изотермой, сопровождаются уменьшением внутренней энергии. Процессы, расположенные между адиабатой и изотермой, имеют отрицательную теплоемкость, так как
Порядок проведения расчетов
Рассмотрим расчет основных термодинамических параметров состояния рабочего тела на основе примеров. Пример 1. Смесь, состоящая из М1 киломолей углекислого газа и М2 киломолей окиси углерода с начальными параметрами р1 = 5 МПа и Т1 = 2000 К, расширяется до конечного объема V2 = εV1. Расширение может осуществляться по изотерме, по адиабате, по политропе с показателем n. Определить газовую постоянную смеси, ее массу и начальный объем, конечные параметры смеси, работу расширения, теплоту процесса, изменение внутренней энергии, энтальпии и энтропии. Дать сводную таблицу результатов и ее анализ. Показать процессы на p-v и T-s диаграммах. Указания. Показатель адиабаты, а, следовательно, изохорную и изобарную теплоемкости принять независящими от температуры. Для расчета необходимо знать молекулярную массу и газовую постоянную смеси газов. Молекулярная масса смеси газов вычисляется как отношение массы смеси (сумма масс компонентов) к числу молей смеси (сумме числа молей компонентов). Необходимые величины для этого расчета имеются в исходных данных к задаче. Газовая постоянная смеси газов вычисляется как отношение универсальной газовой постоянной к молекулярной массе газовой смеси. При определении теплоемкостей воспользоваться формулой для теплоемкости газовой смеси. Показатель адиабаты определить как отношение изобарной и изохорной теплоемкостей газовой смеси. Расчет начального объема, конечных параметров смеси, работы расширения, теплоты процесса, изменения внутренней энергии, энтальпии и энтропии осуществляется с использованием уравнения состояния идеального газа, уравнения первого закона термодинамики, уравнений соответствующих термодинамических процессов (изотермического, адиабатного, политропного). Основные расчетные формулы имеются в данном пособии, а также в рекомендованной для самостоятельного изучения литературе.
Решение. Исходные данные Количества молей компонентов смеси (кмоль): М1=0.1; М2=0.9 Температура газовой смеси (К): T1 =2000 Давление газовой смеси (Па): р1=5∙106 Степень сжатия: ε=20 Показатель политропы: n= 1.12 Молекулярные массы компонентов (кг/кмоль): μ1 = 44 μ2 = 28
Расчёт 1. Расчёт молекулярной массы смеси в кг/кмоль проводим по формуле: 2. Расчёт массы смеси (кг): mсм = М1∙μ1 + М2∙μ2, mсм =29,6. 3. Расчёт газовой постоянной смеси, Дж/(кг К). R=8134/μсм, R=274,797. 4. Определение первоначального объёма смеси (м3): V1 = mсм∙R∙(T1/p1),, V1 =3.254. 5. Расчёт изотермического процесса 5.1. Работа процесса (Дж): Lt= mсм∙(R∙T1∙ln(ε)), Lt=4.873∙107. 5.2. Теплота процесса равна работе процесса (Дж): qt=Lt =4.873∙107. 5.3. Изменение внутренней энергии (Дж): Δut =0. 5.4. Изменение энтальпии (Дж): Δit =0. 5.5. Изменение энтропии (Дж/К): Δst= qt/ T1, Δst =2.437∙104. 6. Расчёт адиабатного процесса. 6.1. Определение показателя адиабаты. 6.1.1. Изобарные и изохорные теплоёмкости компонентов, кДж/(кмоль К) - справочные ср1=37.4 ср2=29.1 cvl =29.1 cv2 = 20.8 6.1.2. Показатель адиабаты 6.2. Работа адиабатного процесса, Дж:
6.3. Теплота адиабатного процесса равно нулю, Дж: qs=0 6.4. Изменение внутренней энергии адиабатного процесса равно работе процесса с обратным знаком, Дж. Δus = -Ls, Δus = -2.896∙107. 6.5. Изменение энтальпии адиабатного процесса, Дж:
6.6. Изменение энтропии в адиабатном процессе равно нулю: Δs=0. 7. Политропный процесс 7.1. Работа политропного процесса (Дж):
7.2. Теплота политропного процесса (Дж) 7.3. Изменение внутренней энергии политропного процесса (Дж): 7.4. Изменение энтальпии политропного процесса: 7.4.1. Изобарная теплоёмкость ср (Дж/(кг К)) и конечная температура Т2 (К) политропного процесса: 7.4.2. Изменение энтальпии (Дж): Δip=mсм∙cp∙(T2-T1), Δip=-1.771∙107. 7.5. Изменение энтропии политропного процесса: 7.5.1. Теплоёмкость политропного процесса сn (Дж/(кг К)):
7.5.2. Изменение энтропии (Дж/К):
Результаты расчётов
Пример 2. Расход газа в поршневом одноступенчатом компрессоре составляет V1 при давлении р1 = 0,1 МПа и температуре t1. При сжатии температура газа повышается на 200 оС. Сжатие происходит по политропе с показателем n. Определить конечное давление, работу сжатия и работу привода компрессора, количество отведенной теплоты, а также теоретическую мощность привода компрессора. Указания. Показатель адиабаты принять постоянной величиной. Расчеты следует вести по формулам для политропного процесса. При расчете работы привода компрессора следует иметь в виду то, что компрессор работает циклично, периодически всасывая и выталкивая рабочее вещество (открытая термодинамическая система). Таким образом при определении работы привода должны быть учтены затраты на смену рабочего вещества в компрессоре. То есть работе привода соответствует располагаемая работа. Теоретическая мощность привода должна соответствовать расходу газа через компрессор. Основные расчетные формулы имеются в данном пособии, а также в рекомендованной для самостоятельного изучения литературе.
Решение. Исходные данные Расход газа через компрессор (м3/мин) – V21 =20. Начальная температура газа (К) – T21= 273. Молекулярная масса газа (кг/кмоль) – μ21=29. Показатель политропы – n2=1.35. Конечная температура политропного сжатия (К) – T22=473. Начальное давление газа (Па) – p21 =105. Показатель адиабаты газа (справочный) – k2 =1.4.
Расчёт 1. Конечное давление при политропном сжатии (Па):
2. Работа сжатия компрессора 2.1. Газовая постоянная воздуха (кДж/кг К):
2.2. Массовый расход газа (кг/с):
2.3. Работа сжатия (кВт):
3. Работа привода компрессора равна располагаемой работе (кВт): L2р=n2 ×L2, L2р = - 94,192. 4. Количество отводимой теплоты - теплота процесса (кВт). 4.1. Изохорная теплоемкость газа (кДж/(кг К)):
4.2. Теплоемкость воздуха в политропном процессе (кДж/(кг К))
4.3. Теплота процесса (кВт): 5. Теоретическая мощность привода компрессора равна располагаемой работе выраженной в кВт: N2 = -L2р N2 = 94,192.
Результаты расчета
Задание для лабораторной работы
Задание 1. Определить газовую постоянную смеси, ее массу и начальный объем, конечные параметры смеси, работу расширения, теплоту процесса, изменение внутренней энергии, энтальпии и энтропии. Дать сводную таблицу результатов и ее анализ. Показать процессы на p-v и T-s диаграммах (построить графики процессов с координатными осями p-v и T-s). Решение провести для своего варианта на базе исходных данных, приведенных в табл.2.1.4. Использовать пример 1 и алгоритм его решения, указанный в §2.1.5. Задание 2. Определить конечное давление, работу сжатия и работу привода компрессора, количество отведенной теплоты, а также теоретическую мощность привода компрессора. Решение провести для своего варианта на базе исходных данных, приведенных в табл.2.1.5. Использовать пример 2 и алгоритм его решения, указанный в §2.1.5. Задание 3. Письменно ответить на следующие вопросы. 1. Привести термодинамические параметры состояния рабочего тела. 2. Дать определения и привести формульные зависимости основных функций состояния. 3. Привести формулировки и формульные зависимости законов (начал) термодинамики. 4. Перечислить и записать условия термодинамических процессов идеальных газов в закрытых системах 5. Как зависит работа от показателя политропы и почему? 6. Как изменятся (численно) результаты расчетов адиабатного процесса, если учесть, что показатель адиабаты зависит от температуры? 7. Как влияет показатель политропы на конечное давление при фиксированных значениях p1, t2 и t1? Указание. Номер варианта указывает преподаватель (при получении работы по электронной почте номер варианта берется по последней цифре зачетной книжки, причем для цифры «0» берется 10 вариант задания).
Структура отчета
По материалам работы каждым студентом составляется отчет по установленной форме с использованием Microsoft WORD. Расчеты, диаграммы, графики, структурно-следственные схемы следует выполнять с использованием ПЭВМ или чертежных принадлежностей. Особое внимание при оформлении отчета студенты должны обратить на составление выводов по выполненной работе. В выводах нужно сопоставить результаты проведенных исследований с известными из теоретического курса закономерностями и выяснить согласованность полученных результатов с теоретическими. Полностью оформленный исполнителем отчет представляется каждым студентом преподавателю на следующем занятии. Отчет по лабораторной работе должен содержать: 1. Титульный лист, оформленный по образцу. 2. Исходные данные. 3. Результаты расчетов по заданиям, графики, таблицы. 4. Ответы на поставленные в задании вопросы. 5. Выводы по заданиям. К отчету прилагаются программы табличного процессора Microsoft EXCEL в электронном виде (если работа выполнялась на ПК). Представленные в отчете результаты, порядок их получения, расчетов и графиков студенты обязаны уметь четко пояснить. За проведенную работу и оформленный отчет преподаватель выставляет дифференцированную оценку.
Исходные данные Таблица 2.1.4 Данные для задания 1 Номер варианта | М1 | М2 | ε=V 1 / V 2 | n | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| кмоль | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 0.1 | 0,9 | 20 | 1.12 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 0.2 | 0,8 | 18 | 1.16 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 0.3 | 0,7 | 16 | 1.27 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 0,4 | 0.6 | 14 | 1.25 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 0,5 | 0,5 | 12 | 1.22 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 0.6 | 0.4 | 10 | 1.55 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 0.7 | 0,3 | 8 | 1.45 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 0.8 | 0,2 | 6 | 1.52 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 0.9 | 0,1 | 14 | 1.28 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 0.5 | 0,5 | 16 | 1,25 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица 2.1.5
Данные для задания 2
| Номер варианта | V1, м3/мин. | t1, 0C | Газ | n |
| 1 | 20 | 0 | Воздух | 1.35 |
| 2 | 25 | 7 | Не | 1,45 |
| 3 | 30 | 10 | О2 | 1.32 |
| 4 | 35 | 12 | N2 | 1.33 |
| 5 | 40 | 15 | СО | 1.35 |
| 6 | 45 | 17 | N2 | 1.34 |
| 7 | 50 | 20 | О2 | 1.29 |
| 8 | 55 | 22 | Не | 1.5 |
| 9 | 60 | 25 | СО2 | 1.28 |
| 10 | 65 | 30 | Воздух | 1.32 |
|
| Поделиться: |

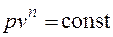 .
.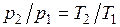 .
.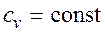 , определяется как (рис.2.1.5):
, определяется как (рис.2.1.5):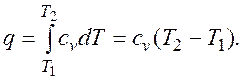
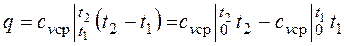 ,
,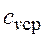 - средняя массовая изохорная теплоемкость в интервале температур от t1 до t2.
- средняя массовая изохорная теплоемкость в интервале температур от t1 до t2.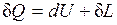 )
)  и
и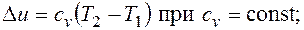
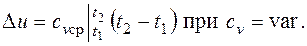
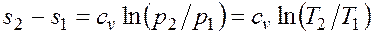 ,
,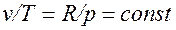 , или
, или 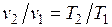 , т.е. в изобарном процессе объем газа пропорционален его абсолютной температуре (закон Гей-Люссака, 1802 г.). На рис.2.1.6 изображен график процесса.
, т.е. в изобарном процессе объем газа пропорционален его абсолютной температуре (закон Гей-Люссака, 1802 г.). На рис.2.1.6 изображен график процесса.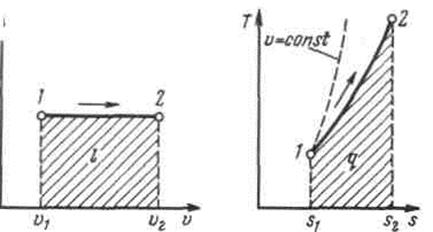
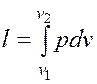 следует, что
следует, что 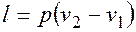 .
.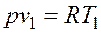 и
и 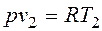 , то одновременно
, то одновременно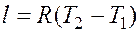
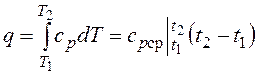 ,
,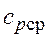 - средняя массовая изобарная теплоемкость в интервале температур от t1 до t2 при
- средняя массовая изобарная теплоемкость в интервале температур от t1 до t2 при 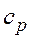 = const
= const 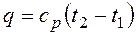 .
.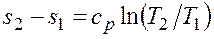 ,
,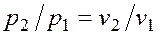 ,
, .
.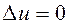 ) и вся подводимая к газу теплота полностью превращается в работу расширения:
) и вся подводимая к газу теплота полностью превращается в работу расширения: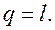
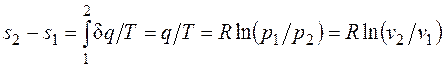 .
.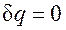 . Для того чтобы осуществить такой процесс, следует либо теплоизолировать газ, т.е. поместить его в адиабатную оболочку, либо провести процесс настолько быстро, чтобы изменение температуры газа, обусловленное его теплообменом с окружающей средой, было пренебрежимо мало по сравнению с изменением температуры, вызванным расширением или сжатием газа. Как правило, это возможно, ибо теплообмен происходит значительно медленнее, чем сжатие или расширение газа.
. Для того чтобы осуществить такой процесс, следует либо теплоизолировать газ, т.е. поместить его в адиабатную оболочку, либо провести процесс настолько быстро, чтобы изменение температуры газа, обусловленное его теплообменом с окружающей средой, было пренебрежимо мало по сравнению с изменением температуры, вызванным расширением или сжатием газа. Как правило, это возможно, ибо теплообмен происходит значительно медленнее, чем сжатие или расширение газа.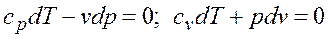 . Поделив первое уравнение на второе, получим
. Поделив первое уравнение на второе, получим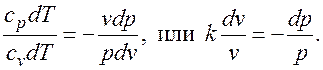
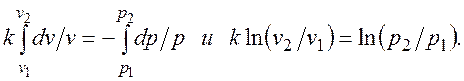
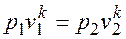 . (2.1.7)
. (2.1.7)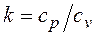 называется показателем адиабаты.
называется показателем адиабаты.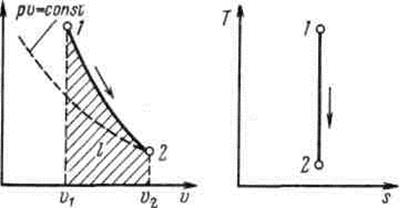
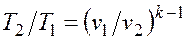 ;
;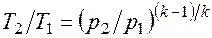 .
.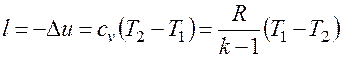 .
.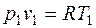 и
и 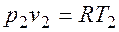 , то
, то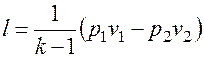 .
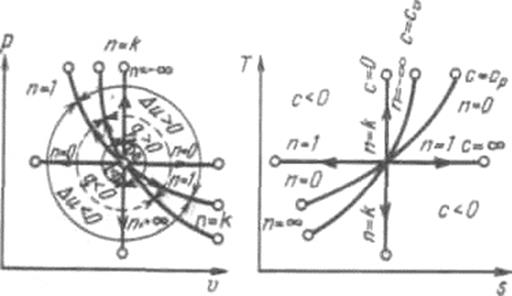
.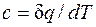 показывает, что теплоемкость адиабатного процесса равна нулю.
показывает, что теплоемкость адиабатного процесса равна нулю.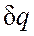 = 0, энтропия рабочего тела не изменяется (ds=0 и s=const). Следовательно, на Т,s-диаграмме адиабатный процесс изображается вертикалью.
= 0, энтропия рабочего тела не изменяется (ds=0 и s=const). Следовательно, на Т,s-диаграмме адиабатный процесс изображается вертикалью.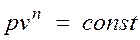 ,
,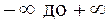 , но для данного процесса он является величиной постоянной.
, но для данного процесса он является величиной постоянной.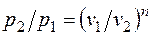 ;
; 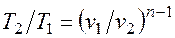 ;
; 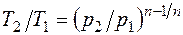 . (2.1.8)
. (2.1.8) .
.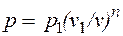 ,
,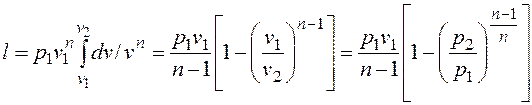 (2.1.9)
(2.1.9)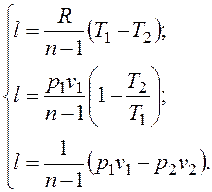
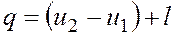 .
.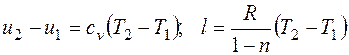 , то
, то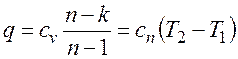 ,
,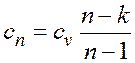
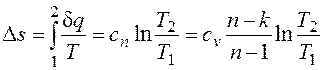 .
.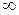 ) делит поле диаграммы на две области: процессы, находящиеся правее изохоры, характеризуются положительной работой, так как сопровождаются расширением рабочего тела; для процессов, расположенных левее изохоры, характерна отрицательная работа.
) делит поле диаграммы на две области: процессы, находящиеся правее изохоры, характеризуются положительной работой, так как сопровождаются расширением рабочего тела; для процессов, расположенных левее изохоры, характерна отрицательная работа.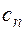
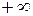
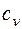
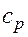
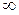
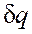 и du (а следовательно, и dT), имеют в этой области противоположные знаки. В таких процессах
и du (а следовательно, и dT), имеют в этой области противоположные знаки. В таких процессах 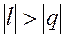 , поэтому на производство работы при расширении тратится не только подводимая теплота, но и часть внутренней энергии рабочего тела.
, поэтому на производство работы при расширении тратится не только подводимая теплота, но и часть внутренней энергии рабочего тела.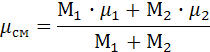 , μсм = 29,6.
, μсм = 29,6.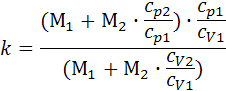 , k = 1.384.
, k = 1.384.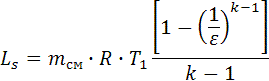 , Ls=2.896∙107.
, Ls=2.896∙107.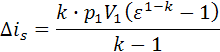 , Δis=-4.008∙107.
, Δis=-4.008∙107.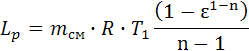 , Lp = 4.094∙107.
, Lp = 4.094∙107.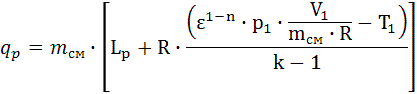 , qp=1.199∙109.
, qp=1.199∙109.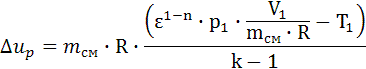 , Δup =-1,28∙107.
, Δup =-1,28∙107.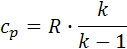 ,
, 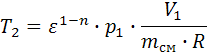
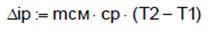 ,
,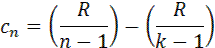 .
.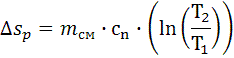 , Δsр=-1.675∙104
, Δsр=-1.675∙104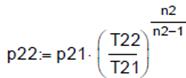 , p22 =8.331∙105
, p22 =8.331∙105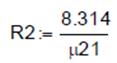 , R2 =0.287.
, R2 =0.287.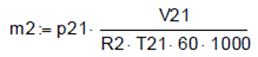 , m2 =0.426.
, m2 =0.426.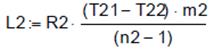 , L2= - 69, 711
, L2= - 69, 711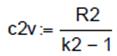 , c2v =0.717.
, c2v =0.717.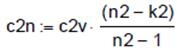 , c2n = -0,102
, c2n = -0,102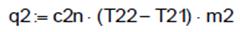 , q2= -8,721.
, q2= -8,721.


