
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 2. Лабораторная работа «Определение основныхСодержание книги
Поиск на нашем сайте
параметров тепломассообмена»
Цель работы
Лабораторная работа выполняется на основе теоретических положений теплотехники, теории теплообмена с использованием табличного процессора Microsoft EXCEL в среде Windows 9*/NT/2000/ХР или с помощью инженерного калькулятора. Цель работы: знакомство с основами теории тепломассообмена; получение умений и навыков: в освоении методики расчета передачи теплоты в процессах теплопроводности, конвекции, теплового излучения, а также в комбинированных процессах теплоотдачи и теплопередачи; в умении делать выводы и давать рекомендации при выборе методов и средств защиты объектов от теплового воздействия; в проведении инженерных расчетов.
Основы теории теплообмена Теплопередача - это процесс переноса теплоты от одного теплоносителя к другому через разделяющую стенку. Теплопередача связана с весьма сложными процессами и при ее изучении необходимо знать законы теории теплообмена и методы анализа, применяемые в физике, термодинамике, гидродинамике и химии. Сложный процесс переноса теплоты разбивают на ряд более простых. Такой прием упрощает его изучение. Кроме того, каждый простой процесс переноса теплоты подчиняется своим законам. Существует три простейших способа передачи теплоты: теплопроводность, конвекция, излучение. Явление теплопроводности состоит в переносе теплоты микрочастицами (молекулами, атомами, электронами и т.п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур. Конвективный теплоперенос (конвекция) наблюдается лишь в жидкостях и газах. Конвекция - это перенос теплоты вместе с макроскопическими объемами вещества. Следует иметь ввиду, что одновременно с конвекцией всегда существует и теплопроводность. Однако конвекция обычно является определяющей, т.к. она интенсивнее теплопроводности. Конвекцией можно передавать теплоту на очень большие расстояния (например, при движении газа по трубам). Движущаяся среда (жидкость или газ), используемая для переноса теплоты, называется теплоносителем. Третьим способом переноса теплоты является излучение. За счет излучения теплота передается во всех лучепрозрачных средах, в том числе и в вакууме. Носителями энергии при теплообмене излучением являются фотоны, излучаемые и поглощаемые телами, участвующими в теплообмене. В большинстве случаев перенос тепла осуществляется несколькими способами одновременно. Например, конвективная теплопередача от газа к стенке практически всегда сопровождается параллельным переносом теплоты излучением.
2.2.2.1. Основные понятия и определения.
Интенсивность переноса теплоты характеризуется плотностью теплового потока. Плотность теплового потока - это количество теплоты, передаваемое в единицу времени через единичную плотность поверхности, q [Вт/м2]. Мощность теплового потока или просто тепловой поток - это количество теплоты, передаваемое в единицу времени через произвольную поверхность F, [Вт]. q=Q/F, Вт/м2 поверхность теплообмена F - это поверхность, через которую происходит передача тепла. Например, при остывании теплоносителя в трубе диаметром d и длиной l, тепло передается от горячего теплоносителя к окружающей среде через цилиндрическую поверхность трубы. В этом случае Перенос теплоты зависит от распределения температуры по объему тела или пространства. Температурным полем называется совокупность мгновенных значений температуры во всех точках тела или системы тел в данный момент времени. Математическое описание температурного поля имеет вид: t=f(x,y,z,t), (2.2.1) где t - температура; x,y,z - пространственные координаты; τ - время. Температурное поле, описываемое приведенным уравнением, называется нестационарным. В этом случае температуры зависят от времени. В том случае, когда распределение температуры в теле не изменяется со временем, температурное поле называется стационарным t=f(x,y,z,), (2.2.2) если температура изменяется только по одной или двум пространственным координатам, то температурное поле называется соответственно одно- и двухмерным: t=f(x,t), Температурные поля (2.2.1) и (2.2.2) называются трехмерными. Поверхность, во всех точках которой температура одинакова, называется изотермической. Изотермические поверхности могут быть замкнутыми, но не могут пересекаться. Быстрее всего температура изменяется при движении в направлении, перпендикулярном изотермической поверхности. Скорость изменения температуры по нормали к изотермической поверхности характеризуется градиентом температуры. Градиент температуры (grad t) - есть вектор, направленный по нормали к изотермической поверхности и численно равный производной пот температуры по этому направлению (рис.2.2.1):
где
Рис. 2.2.1. Расположение градиента температуры и вектора теплового потока относительно изотермы t2=Const температурного поля
Теория теплопроводности. Закон Фурье. Теория теплопроводности рассматривает тело как непрерывную среду. Согласно основному закону теплопроводности - закону Фурье - вектор плотности теплового потока, передаваемого теплопроводностью, пропорционален вектору градиента температуры:
где λ - коэффициент теплопроводности, Вт/(м×К). Он характеризует способность вещества, из которого состоит рассматриваемое тело, проводить теплоту. Знак «-» указывает на противоположное направление вектора теплового потока и вектора градиента температуры. Вектор плотности теплового потока q всегда направлен в сторону наибольшего уменьшения температуры. скалярная величина вектора плотности теплового потока:
Из формулы следует, что коэффициент теплопроводности λ определяет плотность теплового потока при градиенте температуры 1 К/м. Коэффициент теплопроводности является физическим параметром и зависит от химической природы вещества и его физического состояния (плотности, влажности, давления, температуры). Диапазоны изменения
Рис.2.2.2. Теплопроводность при стационарном режиме Однослойная плоская стенка. Рассмотрим однородную плоскую стенку толщиной d, на поверхностях которой поддерживаются температуры tс1 и tс2, причем tс1>tс2 (рис.2.2.3). Температура изменяется только по толщине стенки - по одной координате х, коэффициент теплопроводности
или
где
Рис.2.2.3. Изменение температур по толщине однородной плоской стенки
Распределение температур в плоской однородной стенке - линейное. В большинстве практических задач приближенно предполагается, что коэффициент теплопроводности λ не зависит от температуры и одинаков по всей толщине стенки. значение λ находят в справочниках при средней температуре Тепловой поток (мощность теплового потока) определяется по формуле:
|
||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 143; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.60.175 (0.008 с.) |

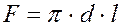 .
.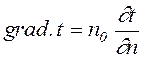 ,
, -единичный вектор, направленный в сторону возрастания температур нормально к изотермической поверхности.
-единичный вектор, направленный в сторону возрастания температур нормально к изотермической поверхности.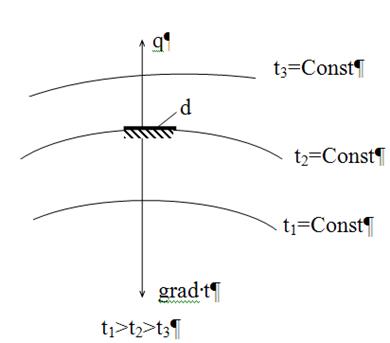
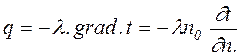 ,
,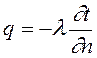 ,
, для различных материалов приведены на рис.2.2.2.
для различных материалов приведены на рис.2.2.2.
 . Теплового потока в этом случае, в соответствии с законом Фурье, определяется по формуле:
. Теплового потока в этом случае, в соответствии с законом Фурье, определяется по формуле: ,
,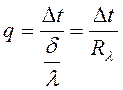 ,
,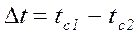 , причем tс1>tс2;
, причем tс1>tс2;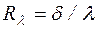 - внутреннее термическое сопротивление теплопроводности стенки, (м2×К)/Вт.
- внутреннее термическое сопротивление теплопроводности стенки, (м2×К)/Вт.
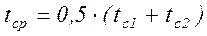 .
.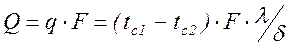 .
.


