
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Использование частных производных для нахождения абсолютных и относительных погрешностей косвенных измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для функций, зависящих от нескольких аргументов, вводят понятия частного и полного дифференциалов. В данном пособии мы не будем вводить эти понятия, а лишь запишем готовые формулы. Так, выражение Чтобы найти частный дифференциал функции нескольких переменных по какому-либо аргументу, нужно найти частную производную функции по этому аргументу и умножить ее на приращение этого аргумента. Пример. Найдите частные дифференциалы функции
Полный дифференциал равен сумме частных дифференциалов:
Полные дифференциалы функций нескольких переменных используют для вычисления абсолютных и относительных погрешностей косвенных измерений. Косвенными называют измерения, проводимые с использованием результатов прямых измерений (снимаемых непосредственно со школ измерительных приборов), числовых констант и связывающих их закономерностей. Фактически косвенные измерения – это расчеты по формулам, в которые входят результаты прямых измерений, как аргументы функции (рассчитываемой величины). Подробнее о проведении измерений и их обработке см. [указать номер в литературе методички по погрешностям] Здесь же мы приведем готовые формулы для расчета абсолютной и относительной погрешностей косвенно измеренной величины.
Пример. Произведены серии прямых измерений диаметра
Найдем средний объем цилиндра:
Выведем формулы для расчета абсолютной и относительной погрешностей данного косвенного измерения. Для этого найдем следующие частные производные:
Составим формулу для вычисления абсолютной погрешности косвенного измерения объема:
Для того, чтобы составить формулу для относительной погрешности косвенного измерения объема, сначала нужно прологарифмировать исходную функцию, так как в формулу для
Теперь составим формулу для вычисления относительной погрешности косвенного измерения объема:
Вычислим погрешности:
Обратим внимание на то, что абсолютная и относительна погрешности связаны соотношением Также учтите, что при расчетах относительная погрешность выражается в долях. Для более удобного восприятия принято выражать ее в процентах В методическом пособии [наша методичка по погрешностям] рассказано, как правильно записать результат измерения, округлив его по правилам. Здесь мы сразу запишем результат косвенного измерения с учетом округления по форме:
Следует отметить, что если формула для расчета в косвенном измерении величины представляет собой произведение или частное прямо измененных величин (как в рассмотренном примере), то выгоднее выводить формулу для расчета относительной погрешности косвенного измерения. Как правило, она получается проще и короче, нежели формула, полученная для расчета абсолютной погрешности этого косвенного измерения. Если же исходная формула представляет собой сумму или разность некоторых слагаемых, то лучше выводить формулу для расчета абсолютной погрешности, формула для расчета относительной погрешности в этом случае получится более сложной. И, как сказано выше, зная величину одной из погрешностей и среднее значение функции легко найти другую погрешность. 2.3. Задания для самостоятельного решения
I. Найдите частные производные функции
II. Найти все вторые частные производные следующих функций:
III. Выведите формулы для расчета абсолютной и относительной погрешностей косвенно измеренной величины. 1) В лабораторной работе по изучению сухого трения коэффициент трения качения, как косвенно измеренная величина, определяется по формуле 2) В лабораторной работе по изучению вязкого трения коэффициент вязкого трения, как косвенно измеренная величина, определяется по формуле
Вместо этих формул нужно написать формулу для расчета коэффициента вязкости!!!
, где
3) Некоторая величина
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 5080; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

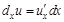 есть частный дифференциал функции, зависящей от нескольких переменных, по аргументу
есть частный дифференциал функции, зависящей от нескольких переменных, по аргументу 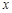 . Аналогично
. Аналогично 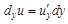 – частный дифференциал функции по аргументу
– частный дифференциал функции по аргументу 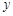 ,
, 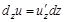 – частный дифференциал функции по аргументу
– частный дифференциал функции по аргументу  .
.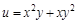 .
.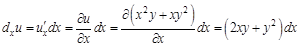 – частный дифференциал функции по аргументу
– частный дифференциал функции по аргументу 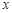 .
.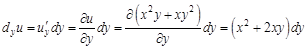 – частный дифференциал функции по аргументу
– частный дифференциал функции по аргументу 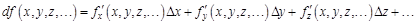
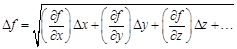 – формула для расчета абсолютной погрешности измерения косвенной величины
– формула для расчета абсолютной погрешности измерения косвенной величины 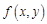 ;
;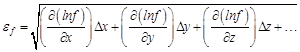 – формула для расчета относительной погрешности измерения косвенной величины
– формула для расчета относительной погрешности измерения косвенной величины  и высоты
и высоты  сплошного цилиндра. Найдены их средние значения
сплошного цилиндра. Найдены их средние значения 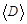 и
и 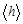 и определены абсолютные погрешности
и определены абсолютные погрешности 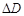 и
и 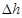 прямых измерений диаметра и высоты. По приведенным численным данным рассчитайте средний объем цилиндра
прямых измерений диаметра и высоты. По приведенным численным данным рассчитайте средний объем цилиндра 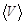 и оцените абсолютную и относительную погрешности этого косвенного измерения.
и оцените абсолютную и относительную погрешности этого косвенного измерения.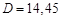 мм,
мм, 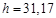 мм,
мм, 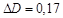 мм,
мм, 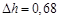 мм
мм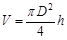 ,
, 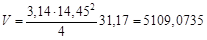 мм 3
мм 3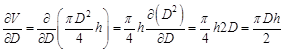 ;
;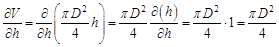 .
.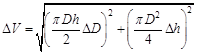 .
. входят частные производные от логарифма функции. Итак:
входят частные производные от логарифма функции. Итак: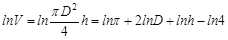 ;
;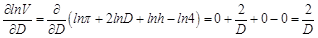 ;
;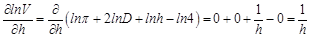 .
.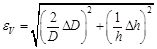 .
.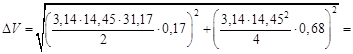
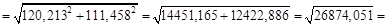
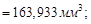
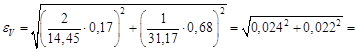
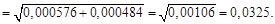
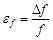 . Поэтому, зная одну из погрешностей и среднее значение функции, легко найти другую погрешность по этому соотношению без вычисления для нее соответствующих частных производных. Предлагаем Вам самостоятельно проделать эти расчеты для рассмотренного примера.
. Поэтому, зная одну из погрешностей и среднее значение функции, легко найти другую погрешность по этому соотношению без вычисления для нее соответствующих частных производных. Предлагаем Вам самостоятельно проделать эти расчеты для рассмотренного примера.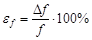 .
.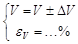 . Имеем:
. Имеем: 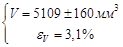
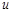 по всем ее переменным:
по всем ее переменным: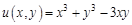
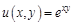
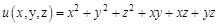
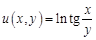
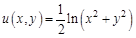
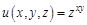
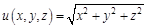
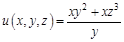
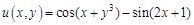
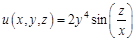
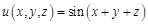
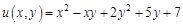
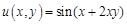
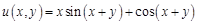
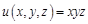
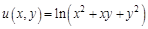
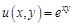
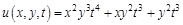
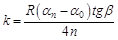 , где
, где 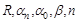 – прямо измененные величины. Выведите формулы для расчета абсолютной и относительной погрешностей косвенного измерения коэффициента
– прямо измененные величины. Выведите формулы для расчета абсолютной и относительной погрешностей косвенного измерения коэффициента 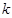 . Оцените, какую из полученных формул было сразу выгоднее выводить. Почему?
. Оцените, какую из полученных формул было сразу выгоднее выводить. Почему?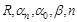 – прямо измененные величины. Оцените, какую из формул для расчета абсолютной или относительной погрешности выгоднее выводить. Выведите ее.
– прямо измененные величины. Оцените, какую из формул для расчета абсолютной или относительной погрешности выгоднее выводить. Выведите ее.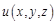 является косвенным измерением и рассчитывается по формуле
является косвенным измерением и рассчитывается по формуле 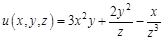 , где
, где 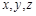 – прямо измененные величины.
– прямо измененные величины.


