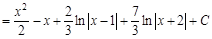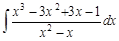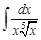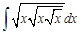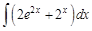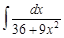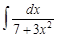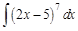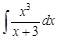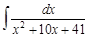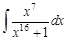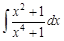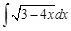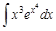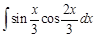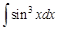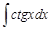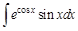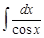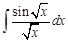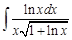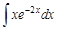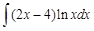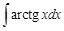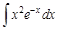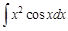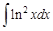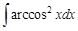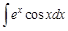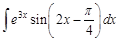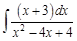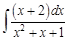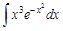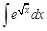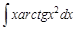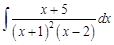Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование рациональных дробейСодержание книги
Поиск на нашем сайте
Метод основан на том, что рациональную дробь можно представить в виде суммы рациональных дробей. Способ интегрирования таких дробей зависит от того, имеет ли знаменатель дроби корни, и является ли дробь правильной. На примерах рассмотрим, как решают такие интегралы. Пример 1. Подынтегральная функция является правильной дробью. Ее знаменатель имеет два корня
Последнюю дробь можно представить, как сумму дробей:
Приводя сумму дробей к общему знаменателю, получим:
Таким образом, получаем, что:
Если дроби равны, следовательно, равны их числители и знаменатели. Тогда:
Раскроем скобки в правой части равенства и приведем подобные слагаемые:
Если многочлены равны, то коэффициенты при переменных в соответствующих степенях тоже равны:
Решая эту систему относительно
При решении последних интегралов «подделали» дифференциал, чтобы интеграл принял табличный вид. При таком «подделывании» дифференциала нужно помнить, что если переменную умножаем на какое-либо число, то нужно и поделить на это число. Причем не нужных по форме множитель можно вынести за знак дифференциала и далее за знак интеграла. Пример 2. В данном случае знаменатель подынтегрального выражение имеет два одинаковых корня
Если дроби равны, следовательно равны их числители и знаменатели. Тогда:
Раскроем скобки в правой части равенства и приведем подобные слагаемые:
Если многочлены равны, то коэффициенты при переменных в соответствующих степенях тоже равны:
Решая эту систему относительно
Пример 3. В данном случае знаменатель подынтегрального выражение не имеет действительных корней. Представим подынтегральную функцию в виде следующей суммы:
Если дроби равны, следовательно равны их числители и знаменатели. Тогда:
Если многочлены равны, то коэффициенты при переменных в соответствующих степенях тоже равны:
Решая эту систему относительно
Пример 4. Теперь мы имеем дело с неправильной рациональной дробью под интегралом. В таких случаях неправильную дробь представляют в виде целой части и правильной рациональной дроби. В данном случае получим:
Теперь интеграл можно представить в виде суммы:
и теперь работать с правильной рациональной дробью во втором интеграле. Многочлен в знаменателе этой дроби имеет два корня
Если дроби равны, следовательно равны их числители и знаменатели. Тогда:
Раскроем скобки в правой части равенства и приведем подобные слагаемые:
Если многочлены равны, то коэффициенты при переменных в соответствующих степенях тоже равны:
Решая эту систему относительно
3.6. Задания для самостоятельного решения
I. Решите следующие интегралы методом непосредственного интегрирования
II. Решите следующие интегралы методом замены переменной
III. Найдите интегралы, применяя метод интегрирования по частям
IV. Найдите интегралы от рациональных дробей
IV. Применяя различные методы, найдите интегралы
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 297; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.102.0 (0.006 с.) |

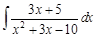
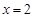 и
и  (это можно выяснить, решив квадратное уравнение, которое представляет знаменатель). Тогда подынтегральную дробь можно представить так:
(это можно выяснить, решив квадратное уравнение, которое представляет знаменатель). Тогда подынтегральную дробь можно представить так:
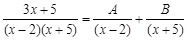
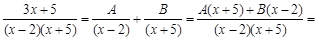

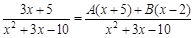
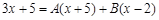
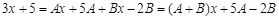
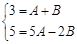
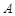 и
и 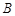 , получим, что
, получим, что 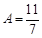 , а
, а 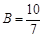 . Зная коэффициенты
. Зная коэффициенты  и
и 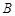 , мы может заменить исходную подынтегральную дробь на сумму дробей. При этом получим более простые интегралы:
, мы может заменить исходную подынтегральную дробь на сумму дробей. При этом получим более простые интегралы: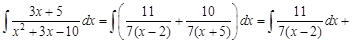
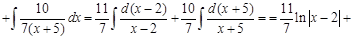
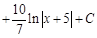
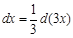 . Здесь подправили дифференциал, помножив его на 3, и компенсировали это изменение, поделив дифференциал на 3. А вот прибавить или вычесть число под дифференциалом можно без исправлений. Действительно,
. Здесь подправили дифференциал, помножив его на 3, и компенсировали это изменение, поделив дифференциал на 3. А вот прибавить или вычесть число под дифференциалом можно без исправлений. Действительно, 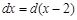 , так как
, так как 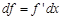 . В нашем примере
. В нашем примере 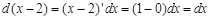 . Именно так и поступили, решая последние интегралы в приведенном выше примере.
. Именно так и поступили, решая последние интегралы в приведенном выше примере.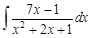
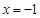 , и подынтегральную дробь нужно представить в такой суммы:
, и подынтегральную дробь нужно представить в такой суммы: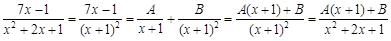
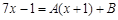
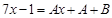
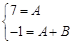
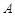 и
и 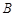 , получим, что
, получим, что 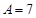 , а
, а  . Зная коэффициенты
. Зная коэффициенты  и
и 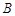 , мы может заменить исходную подынтегральную дробь на сумму дробей. При этом получим более простые интегралы:
, мы может заменить исходную подынтегральную дробь на сумму дробей. При этом получим более простые интегралы: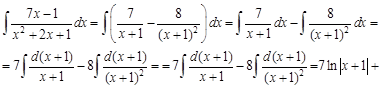
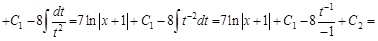
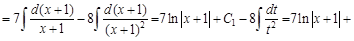
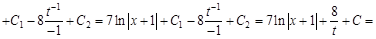


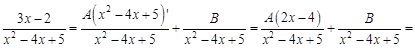


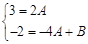
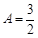 , а
, а 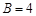 . Зная коэффициенты
. Зная коэффициенты 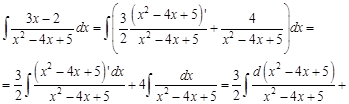
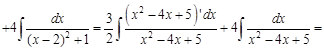
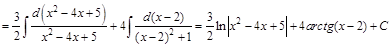

 .
. .
.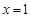 и
и 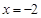 . Имеем:
. Имеем:

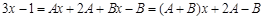

 , а
, а  . Зная коэффициенты
. Зная коэффициенты