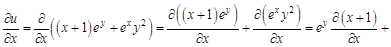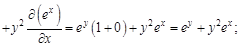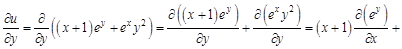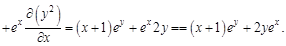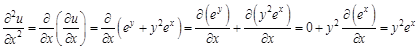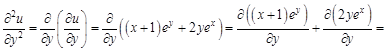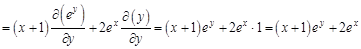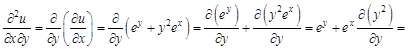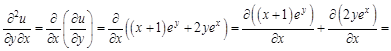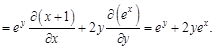Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о частных производных функцииСодержание книги
Поиск на нашем сайте Нескольких переменных Мы уже отмечали, что реальные процессы сложны и многогранны. На их протекание влияет множество факторов, что при математическом описании отражается в зависимости функции от нескольких переменных. Но нельзя изучать влияние на функцию всех переменных одновременно. Это делают поочередно, рассматривая, как изменяется результат (функция) при изменении одного фактора (одной переменной), затем другого фактора (следующей переменной) и т.д. Одновременное же изучение зависимости функции от нескольких факторов может дать неверный результат, так как одни факторы могут усиливать друг друга, другие ослаблять или компенсировать. Поэтому и возникает задача изучения быстроты изменения результата (функции) от каждого конкретного, влияющего на нее фактора (переменной). Нахождение изменения функции в частности от данной, конкретной переменной – по сути и есть вычисление частной производной. Частной производной функции
Аналогично дают определение частной производной функции по любому другому ее аргументу, например, по
Обращаем внимание на то, что при вычислении частной производной функции по какому-либо ее аргументу, все остальные аргументы считают постоянными величинами. Фактически частную производную ищут как обыкновенную производную функции одной переменной, полагая остальные переменные константами. Выражения Рассмотрим примеры нахождения частных производных функций. Будем помнить, что те аргументы, по которым в данном случае не ищем производную, считаем константами. А все постоянные величины можно выносить за знак производной. Поэтому для того, чтобы было проще решать, сначала будем выносить все константы за знак производной, а затем искать производную от оставшегося выражения. Пример 1.
Отметим, что второе слагаемое функции
Напомним, что производную от а) представить ее как степенную функцию, стоящую в числителе б) найти производную этой функции по правилу для производной частного:
Как видим, результаты получаются одинаковые. Пример 2.
Пример 3.
Так же, как и для функций одной переменной, для функций, зависящих от нескольких переменных, можно искать производные высших порядков. Рассмотрим это на примере функции двух переменных. Частными производными второго порядка или вторыми частными производными функции Частные производные высших порядков, взятые только по одной переменной, называют чистыми производными, а те, что берут по разным переменным, называют смешанными производными. Частные производные второго порядка функции двух переменных обозначают так:
Как видим, вторые смешанные производные отличаются друг от друга порядком дифференцирования. Отметим, что существует теорема о том, что, если вторые смешанные производные функции двух переменных существуют и непрерывны в точке дифференцирования, то они равны между собой. Покажем вычисление вторых производных функции двух переменных на примере. Пример 1.
Теперь найдем вторые частные производные функции. Сначала дважды по
Теперь дважды по
А теперь найдем смешанные производные второго порядка. Сначала по
Найдем смешанную производную второго порядка по
Видим, что смешанные производные второго порядка равны. Пример 2. Найдем частные производные первого порядка.
Найдем частные производные второго порядка.
Видим, что смешанные производные второго порядка равны. Можно искать частные производные функций и более высоких порядков. Аналогично рассмотренному выше находят частные производные функций, зависящих от трех и более аргументов.
|
||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

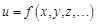 по аргументу
по аргументу 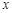 называют предел отношения
называют предел отношения 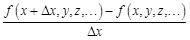 при стремлении приращения
при стремлении приращения 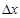 к нулю и записывают:
к нулю и записывают: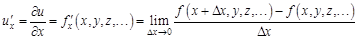 .
.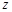 :
: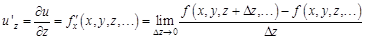 .
.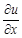 ,
, 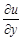 ,
, 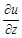 не воспринимают как отношение дифференциалов, их рассматривают как неразрывные символы частных производных.
не воспринимают как отношение дифференциалов, их рассматривают как неразрывные символы частных производных.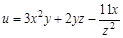 . Найдите частные производные функции
. Найдите частные производные функции 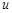 по всем ее переменным.
по всем ее переменным.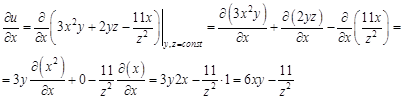
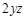 не содержит переменной
не содержит переменной 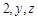 сейчас считаем константами, а производная постоянной величины равна нулю.
сейчас считаем константами, а производная постоянной величины равна нулю.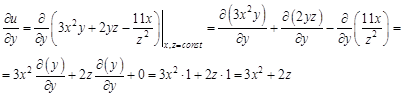
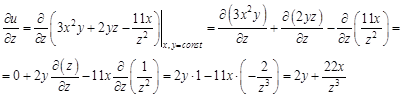
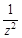 можно найти двумя способами:
можно найти двумя способами: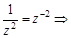
 ;
;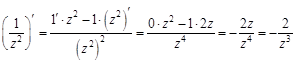 .
.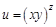 . Найдите частные производные функции
. Найдите частные производные функции 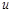 по всем ее переменным.
по всем ее переменным.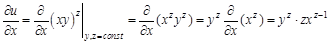
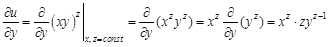
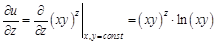
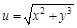 . Найдите частные производные функции
. Найдите частные производные функции 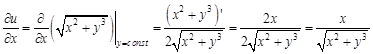
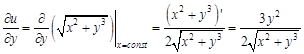
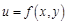 называют частные производные от частных производных этой функции первого порядка.
называют частные производные от частных производных этой функции первого порядка.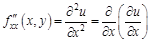 – вторая частная производная функции
– вторая частная производная функции 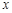 , то есть сначала взяли первую частную производную функции
, то есть сначала взяли первую частную производную функции 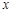 , а затем взяли частную производную по переменной
, а затем взяли частную производную по переменной 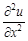 читают так «дэ два у по дэ икс дважды»; обращаем внимание, что в этой записи цифры 2 означают порядок производной (вверху) и сколько раз взята производная данной функции по переменной
читают так «дэ два у по дэ икс дважды»; обращаем внимание, что в этой записи цифры 2 означают порядок производной (вверху) и сколько раз взята производная данной функции по переменной 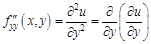 – вторая частная производная функции
– вторая частная производная функции 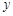 ;
;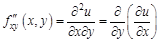 – вторая смешанная производная функции
– вторая смешанная производная функции 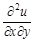 читают так «дэ два у по дэ икс дэ игрек»;
читают так «дэ два у по дэ икс дэ игрек»;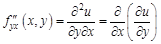 – вторая смешанная производная функции
– вторая смешанная производная функции 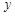 , а затем от полученной производной взяли частную производную по переменной
, а затем от полученной производной взяли частную производную по переменной 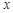 ; запись
; запись 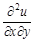 читают так «дэ два у по дэ икс дэ игрек».
читают так «дэ два у по дэ икс дэ игрек». . Найдем вторые частные производные этой функции. Для этого сначала найдем ее первые частные производные.
. Найдем вторые частные производные этой функции. Для этого сначала найдем ее первые частные производные.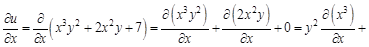
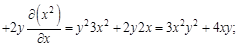
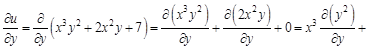
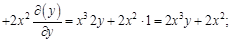
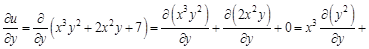
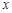 :
: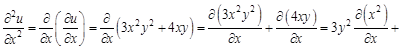
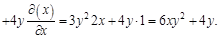
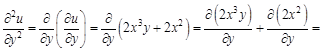
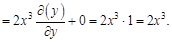
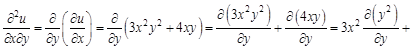
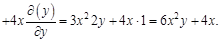
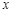 :
: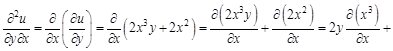
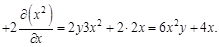
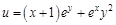 . Найти для указанной функции все частные производные второго порядка.
. Найти для указанной функции все частные производные второго порядка.