
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения первого порядка с разделяющимися переменными ⇐ ПредыдущаяСтр 10 из 10
Дифференциальным уравнением первого порядка с разделяющимися переменными называют уравнение, которое может быть представлено в виде: Решение этого уравнения основано на разделении переменныхпо разным частям уравнения, то есть на преобразовании уравнения к такому виду, когда искомая функция
Разделим обе части уравнения на функции
Заметим, что дифференциалы могут стоять только в числителе. Для решения этого уравнения достаточно проинтегрировать его левую и правую части:
В результате получим общее решение исходного дифференциального уравнения в неявном виде:
Рассмотрим решение этого вида дифференциальных уравнений на примерах. Пример 1. Решите уравнение Данное уравнение является дифференциальным уравнением первого порядка (так как содержит производную первого порядка Если производную
Разделим переменные, то есть перенесем все, что касается
Чтобы решить это уравнение проинтегрируем его:
Константы
Получили общее решение нашего дифференциального уравнения. Это множество функций указанного вида с различными коэффициентами
Используя начальное условие
Мы нашли определенное значение произвольной постоянной
Пример 2. Решите уравнение Запишем производную
Разделим переменные, получим дифференциальное уравнение с разделенными переменными:
Чтобы решить это уравнение проинтегрируем его:
В левой части воспользуемся определением дифференциала функции
Обозначим
В решении константы
Получили общее решение дифференциального уравнения. Это множество функций указанного вида с различными коэффициентами
Мы нашли определенное значение произвольной постоянной
Мы рассмотрели абстрактные примеры решения обыкновенных дифференциальных уравнений с разделяющимися переменными. Теперь обратимся к уравнениям, описывающим реальную действительность. Уже отмечалось, что протекающие в окружающем нас мире процессы многогранны. Их описание часто является сложной задачей. Для облегчения решения таких задач применяют модели – упрощения реальных объектов, процессов, явлений. Подробнее о моделировании биофизических процессов см. [Антонов В.Ф., Черныш А.М. Физика и биофизика: Учебник / Антонов В.Ф., Черныш А.М., Козлова Е.К., Коржуев А.В. – ГЭОТАР-Медиа, 2008.], [Ремизов А.Н. Медицинская и биологическая физика: Учеб. для мед. спец. Вузов. – М.: Высш. Школа, 1999.]. Здесь же мы рассмотрим решение наиболее простых дифференциальных уравнений, описывающих некоторые процессы, происходящие в биологических системах.
Пример 3. Модель изменения численности популяции (модель Мальтуса). Кратко опишем модель. Реальная система: некоторая популяция одного вида (микроорганизмы, зайцы и т.п.), в которой происходят жизненные процессы во всем их многообразии. Задача: найти закон изменения численности популяции с течением времени, если в начальный момент времени численность популяция составляет Допущения: 1) пусть существуют только процессы размножения и естественной гибели членов популяции, и скорости этих процессов пропорциональны численности особей в данный момент времени; 2) не будем учитывать результаты биохимических и физиологических процессов; 3) не учитываем внутривидовую борьбу, то есть борьбу между особями популяции за место обитания, за пищу, за партнера и пр.; 4) рассматриваем только одну популяцию, то есть не учитываем межвидовую борьбу, нет хищников. Введем следующие обозначения:
Составим уравнение баланса:
Получили обыкновенное дифференциальное уравнение первого порядка с разделяющимися переменными. В правой части вынесем
Разделим переменные в этом уравнении и решим его:
Мы получили общее решение данного дифференциального уравнения. Теперь найдем частное решение нашего уравнения. Для этого, используя условие, что в начальный момент времени численность популяции составляла
Окончательно получаем:
Анализ полученного уравнения, его графическое представление, границы применимости модели Мальтуса будут рассмотрены на практических занятиях. Пример 4. Модель изменения численности популяции с учетом внутривидовой конкуренции (модель Ферхюльста). Данная модель отличается от модели Мальтуса отсутствием 3-го допущения, то есть учитывает внутривидовую борьбу. Соответственно в обозначениях при описании модели появится еще одна величина. Это убыль популяции за счет конкуренции между особями, которая пропорциональна вероятности встречи двух особей,
Разделим переменные:
Для решения проинтегрируем полученное уравнение:
В левой части равенства стоит интеграл рациональной дроби. Найдем его отдельно (см. п. 3.5). Представим подынтегральную дробь в виде суммы рациональных дробей:
Найдем коэффициенты
С учетом найденных коэффициентов запишем интегральное равенство:
Теперь найдем полученные интегралы:
В решении сняты знаки модуля, так как численность популяции не может быть отрицательной. Если из последней формулы выразить
Получили частное решение дифференциального уравнения. Эта формула является законом изменения численности популяции в условиях, обозначенных в задаче. Анализ полученного уравнения, его графическое представление, границы применимости модели Ферхюльста будут рассмотрены на практических занятиях. Для нахождения частного решения дифференциального уравнения можно поступить иначе, если известны конкретные значения аргумента и соответствующие им значения рассматриваемой функции. Тогда можно вычислить определенный интеграл с использованием этих условий, и сразу выразить искомую функцию, которая и будет являться частным решением дифференциального уравнения. В нашей задаче к указанным конкретным значениям можно отнести знание величины численности популяции
Подставим пределы интегрирования и выразим функцию
Получили формулу, такую же, как и в рассуждениях выше. Если выразим из нее Пример 5. Модель изменения массы лекарственного препарата в крови человека при инъекции, инфузии и комбинированном введении вещества (фармакокинетическая модель). В рамках этой модели рассмотрим три случая, соответствующие различным способам введения лекарственного препарата в кровь: однократное введение лекарственного препарата – инъекция (что соответствует случаю, когда пациенту сделали только укол), непрерывное введение препарата с постоянной скоростью – инфузия (это соответствует случаю, когда пациенту поставили только капельницу) и сочетание инъекции и инфузии (когда пациенту сделали укол и одновременно поставили капельницу). Упрощая процессы, протекающие в организме человека при введении лекарственного препарата, сделаем следующие допущения: 1) не будем рассматривать систему органов, через которые последовательно проходит лекарство. Исключим многостадийность процессов ввода, переноса, вывода лекарственного вещества; 2) не будем учитывать молекулярные механизмы процессов такие, как проницаемость вещества, химические превращения и пр.;
3) процессы ввода лекарственного препарата в кровь и вывода его из крови сведем к скорости поступления препарата в кровь и скорости его выхода из крови. Учтем, что скорость выведения препарата из крови пропорциональна его массе в крови в данный момент времени. 4) будем считать процесс инъекции мгновенным, то есть в момент времени Для описания модели введем следующие обозначения:
Составим уравнение баланса:
Это общее уравнение. Рассматривая перечисленные случаи, мы будем накладывать на него некоторые условия и получать уравнение для конкретного случая. Перед слагаемым 1) Инъекция. Считаем, что лекарственный препарат вводится однократно мгновенно. Следовательно, скорость ввода препарата равна нулю
Это обыкновенное дифференциальное уравнение первого порядка с разделяющимися переменными. Решим его.
Получили общее решение дифференциального уравнения. Найдем частное решение, полагая, что в начальный момент времени
Эта функция есть частное решение дифференциального уравнения. Она представляет собой закон, описывающий изменение массы лекарственного препарата в крови при инъекции в соответствии с заданной моделью. Можно получить этот же закон, решая определенные интегралы в левой и правой частях уравнения с учетом начального условия
Анализ полученного уравнения, его графическое представление, границы применимости модели будут рассмотрены на практических занятиях. 2) Инфузия. В этом случае в начальный момент времени лекарственного препарата в крови нет
Получили общее решение дифференциального уравнения. Найдем частное решение, полагая, что в начальный момент времени
Подставим значение
Эта функция есть частное решение дифференциального уравнения. Она представляет собой закон, описывающий изменение массы лекарственного препарата в крови при инфузии в соответствии с заданной моделью. Можно получить этот же закон, решая определенные интегралы в левой и правой частях уравнения с учетом начального условия
3) Сочетание инъекции и инфузии. В этом случае в начальный момент времени в кровь пациента мгновенно вводится некоторая масса лекарственного препарата
Получили общее решение дифференциального уравнения. Найдем частное решение, полагая, что в начальный момент времени Подставим значение
Эта функция есть частное решение дифференциального уравнения. Она представляет собой закон, описывающий изменение массы лекарственного препарата в крови при сочетании инъекции и инфузии в соответствии с заданной моделью. Можно получить этот же закон, решая определенные интегралы в левой и правой частях уравнения с учетом начального условия
Анализ полученного уравнения, его графическое представление, границы применимости модели будут рассмотрены на практических занятиях.
4.3. Задания для самостоятельного решения
I. Найдите общие и частные решения обыкновенных дифференциальных уравнений первого порядка с разделяющимися переменными:
II. Составьте дифференциальное уравнение для решения задачи, найдите его общее и частное решения и проанализируйте полученные результаты. 1) Скорость охлаждения тела пропорциональна разности температур тела и окружающей среды. До какой температуры охладится тело за 30 минут, если за 10 минут оно охладилось от 2) Уменьшение интенсивности света при прохождении через поглощающее вещество пропорционально интенсивности падающего света и толщине поглощающего слоя. Найдите закон убывания интенсивности света, если известно, что при прохождении слоя 3) Найдите закон убывания массы лекарственного препарата в организме человека после инъекции, если через 1 час после введения 10 мг препарата его масса в организме человека уменьшилась вдвое. Какое количество препарата останется в организме через 2 часа. 4) Найдите закон изменения концентрации лекарственного препарата в крове человека после инфузии. Какова будет концентрация препарата в крови через 20 минут, после того, как поставили капельницу, если через 10 минут его концентрация была,,,??? Определите максимальную концентрацию препарата в крови, учитывая, что вместе с тем, что лекарство поступает в организм человека, оно параллельно выводится из крови.
Литература
1. Антонов В.Ф., Черныш А.М. Физика и биофизика: Учебник / Антонов В.Ф., Черныш А.М., Козлова Е.К., Коржуев А.В. – М: ГЭОТАР-Медиа, 2009. – 480 с. 2. Баврин И.И. Высшая математика для химиков, биологов и медиков: Учебник и практикум / И.И. Баврин. – 2-е изд., испр. и доп. – Электрон. дан. – Москва: Издательство Юрайт, 2019. – 398 с. – Режим доступа: https://www.biblio-online.ru. 3. Выгодский М.Я. Справочник по высшей математике. – М.: АСТ: Астрель, 2008. – 991 с. 4. Гюнтер Н.М., Кузьмин Р.О. Сборник задач по высшей математике. 3 тома. – 13-е изд. перераб. – М.: Государственное издательство физико-математической литературы, 1958. 5. Данко П.Е. Высшая математика в упражнениях и задачах: учеб. пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова, С.П. Данко. – 7-е изд. – Москва: АСТ: Мир и Образование, 2016. – 815 с. 6. Зельдович Я.Б. Высшая математика для начинающих и ее приложения к физике / Я.Б. Зельдович. – 4-е изд., стер. – М.: Наука, 1968. – 576 с. 7. Краткий курс по высшей математике: учеб. пособ. / под ред. Ю.Н. Владимирова. – М.: Окей-книга, 2007. – 220 с. 8. Математика. Алгебра и элементарные функции: учеб. пособ. / Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н.; под ред. Г.Н. Яковлева. – М.: Агар, 1999. – 426 с. 9. Морозов Ю.В. Основы высшей математики и статистики: Учебник. – М.: Медицина, 1998. – 232 с. 10. Ремизов А.Н., Максина А.Г. Сборник задач по медицинской и биологической физике: учеб. пособ. для вузов. – 2-е изд., перераб. и доп. – М.: Дрофа, 2001. – 192 с. 11. Ремизов А.Н. Медицинская и биологическая физика: Учеб. для мед. спец. Вузов. – 3-е изд. испр. М.: Высш. Школа, 1999. – 616 с. 12. Шипачев В.С. Высшая математика: полный курс: учебник для академического бакалавриата: рекомендовано Учебно-методическим отделом высшего образования в качестве учебника для студентов высших учебных заведений, обучающихся по всем направлениям и специальностям / В.С. Шипачев; под ред. акад. А.Н. Тихонова; Московский государственный университет им. М.В. Ломоносова. – 4-е изд., испр. и доп. – Москва: Юрайт, 2015. – 607 с. 13. Наша методичка по погрешностям? Возможно, стоит что-то убрать, чтобы литература умещалась на одной странице или, наоборот, добавить, чтобы была на двух. Учебное издание Манина Елена Анатольевна Шадрин Геннадий Анатольевич
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 225; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.162.179 (0.096 с.) |

 и ее дифференциал
и ее дифференциал  представлены только в одной части уравнения, а аргумент
представлены только в одной части уравнения, а аргумент 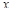 и его дифференциал
и его дифференциал  – в другой. Заметим, что производную
– в другой. Заметим, что производную 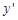 можно записать как
можно записать как 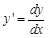 , откуда и появляются дифференциалы
, откуда и появляются дифференциалы  . Тогда уравнение принимает вид:
. Тогда уравнение принимает вид: .
.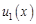 и
и 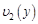 , дополнительно полагая, что они не равны нулю. Получим уравнение, называемое дифференциальным уравнением с разделенными переменными:
, дополнительно полагая, что они не равны нулю. Получим уравнение, называемое дифференциальным уравнением с разделенными переменными: .
.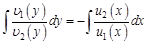 .
.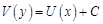 .
. и найдите его частное решение, удовлетворяющее условию
и найдите его частное решение, удовлетворяющее условию  .
.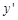 ) с разделяющимися переменными. Обратимся к общему виду таких уравнений:
) с разделяющимися переменными. Обратимся к общему виду таких уравнений: 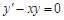 , то видно, что в нашем случае стоящие в уравнении функции имеют вид:
, то видно, что в нашем случае стоящие в уравнении функции имеют вид: 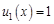 ,
, 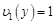 ,
,  ,
, 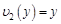 .
. записать через дифференциалы
записать через дифференциалы 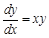 .
. в одну часть уравнения, а что касается
в одну часть уравнения, а что касается 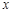 в другую. При это помним, что дифференциалы
в другую. При это помним, что дифференциалы 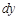 могут быть только в числителе. Получим дифференциальное уравнение с разделенными переменными:
могут быть только в числителе. Получим дифференциальное уравнение с разделенными переменными: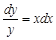 .
.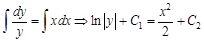 .
.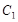 и
и 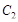 можно перенести в одну часть уравнения, объединить и представить в удобном виде. В нашем случае обозначим общую константу
можно перенести в одну часть уравнения, объединить и представить в удобном виде. В нашем случае обозначим общую константу 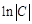 . Это целесообразно делать с целью упрощения дальнейших преобразований в тех случаях, когда при интегрировании дифференциального уравнения с разделенными переменными в левой или правой частях уравнения появляются логарифмы. Тогда имеем:
. Это целесообразно делать с целью упрощения дальнейших преобразований в тех случаях, когда при интегрировании дифференциального уравнения с разделенными переменными в левой или правой частях уравнения появляются логарифмы. Тогда имеем: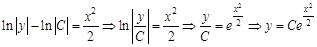 .
.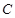 .
.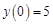 , из общего решения найдем частное решение дифференциального уравнения:
, из общего решения найдем частное решение дифференциального уравнения: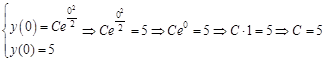 .
. и можем записать соответствующее искомое частное решение дифференциального уравнения:
и можем записать соответствующее искомое частное решение дифференциального уравнения: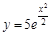 .
.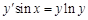 и найдите его частное решение, удовлетворяющее условию
и найдите его частное решение, удовлетворяющее условию  .
.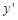 через дифференциалы
через дифференциалы 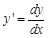 , тогда уравнение примет вид:
, тогда уравнение примет вид: .
.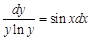 .
.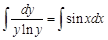 .
. . В нашем случае
. В нашем случае 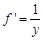 , тогда
, тогда  , следовательно
, следовательно  можно заменить на
можно заменить на 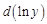 . Получим:
. Получим: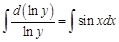 .
.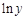 через
через 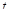 и найдем интегралы:
и найдем интегралы: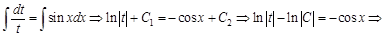
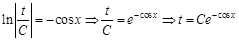
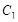 и
и 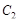 перенесли в одну часть уравнения, объединили и представили в виде общей константы
перенесли в одну часть уравнения, объединили и представили в виде общей константы 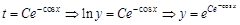 .
. и найдем частное решение дифференциального уравнения:
и найдем частное решение дифференциального уравнения: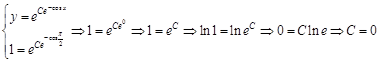 .
.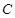 и можем записать соответствующее искомое частное решение дифференциального уравнения:
и можем записать соответствующее искомое частное решение дифференциального уравнения: .
. .
.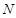 – численность популяции в данный момент времени
– численность популяции в данный момент времени 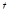 ,
, – коэффициент размножения,
– коэффициент размножения,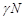 – прирост численности популяции ко времени
– прирост численности популяции ко времени  – коэффициент естественной гибели,
– коэффициент естественной гибели,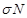 – естественная убыль популяции ко времени
– естественная убыль популяции ко времени 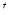 ,
,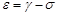 – коэффициент изменения численности популяции,
– коэффициент изменения численности популяции, – скорость изменения численности популяции.
– скорость изменения численности популяции. .
.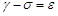 , запишем:
, запишем: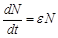 .
.
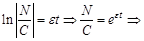
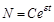 .
. особей, определим значение произвольной постоянной
особей, определим значение произвольной постоянной 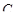 :
: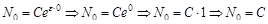 .
. .
.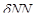 (см. пример 2). Тогда уравнение баланса примет вид:
(см. пример 2). Тогда уравнение баланса примет вид: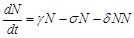 или
или 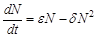 .
.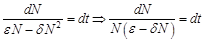 .
.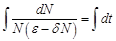 .
. .
.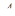 и
и 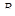 :
: ;
;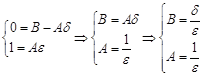 .
.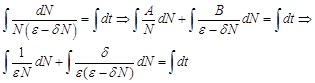
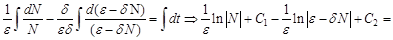
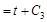
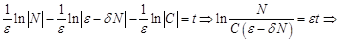
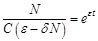
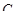 . Для этого используем условие, что в начальный момент времени
. Для этого используем условие, что в начальный момент времени 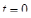 численность популяции составляла
численность популяции составляла  особей:
особей: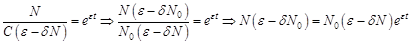
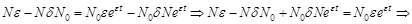
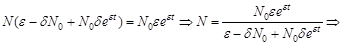
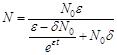 .
. в начальный момент времени
в начальный момент времени  , то есть
, то есть 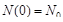 . Вернемся к интегральному уравнению после замены его левой части двумя дробями и найдем определенный интеграл, используя данные о рассматриваемой системе в начальный момент времени:
. Вернемся к интегральному уравнению после замены его левой части двумя дробями и найдем определенный интеграл, используя данные о рассматриваемой системе в начальный момент времени: .
.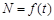 . Снимем знаки модуля, так как численность популяции не может быть отрицательной:
. Снимем знаки модуля, так как численность популяции не может быть отрицательной: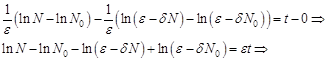
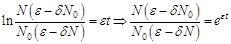
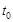 в крови появляется масса препарата
в крови появляется масса препарата 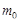 .
.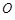 – скорость ввода лекарственного препарата в кровь;
– скорость ввода лекарственного препарата в кровь;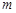 – массе препарата в крови в данный момент времени
– массе препарата в крови в данный момент времени 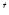 ;
;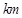 – скорость вывода препарата из крови (в соответствии с п. 3 сделанных допущений пропорциональна массе препарата в крови в данный момент времени,
– скорость вывода препарата из крови (в соответствии с п. 3 сделанных допущений пропорциональна массе препарата в крови в данный момент времени, 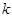 – коэффициент пропорциональности);
– коэффициент пропорциональности);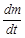 – скорость изменения массы лекарственного препарата в крови с течением времени.
– скорость изменения массы лекарственного препарата в крови с течением времени.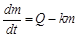 .
.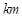 стоит знак минус, что означает убыль препарата в крови.
стоит знак минус, что означает убыль препарата в крови.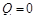 . Тогда из общего уравнения получаем:
. Тогда из общего уравнения получаем: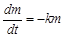 .
.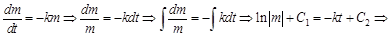
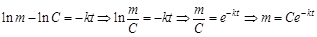 .
. масса лекарственного препарата в крови равна
масса лекарственного препарата в крови равна  :
: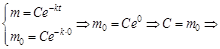
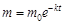 .
.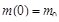 . Покажем это:
. Покажем это:
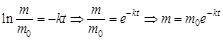
 , он вводится постепенно с постоянной скоростью
, он вводится постепенно с постоянной скоростью  . Параллельно отработанный препарат выводится из крови. Тогда общее дифференциальное уравнение фармакокинетической модели сохраняет свой вид. Решим его:
. Параллельно отработанный препарат выводится из крови. Тогда общее дифференциальное уравнение фармакокинетической модели сохраняет свой вид. Решим его: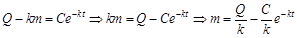
 :
: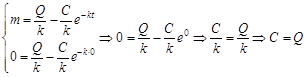 .
.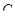 в общее решение:
в общее решение: .
.
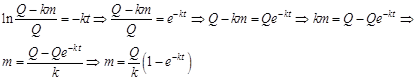 Анализ полученного уравнения, его графическое представление, границы применимости модели будут рассмотрены на практических занятиях.
Анализ полученного уравнения, его графическое представление, границы применимости модели будут рассмотрены на практических занятиях. , полученная порция сразу же начинает выводиться из крови и параллельно через капельницу в кровь добавляют лекарство. Общий вид дифференциального уравнения, описывающего модель сохраняется, но меняются начальные условия. Теперь
, полученная порция сразу же начинает выводиться из крови и параллельно через капельницу в кровь добавляют лекарство. Общий вид дифференциального уравнения, описывающего модель сохраняется, но меняются начальные условия. Теперь 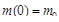 , присутствует
, присутствует  . Решим уравнение в данном случае:
. Решим уравнение в данном случае: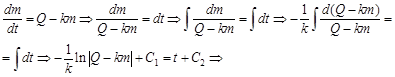
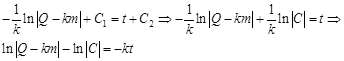

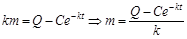
 :
: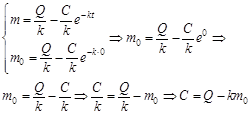 .
. в общее решение:
в общее решение:


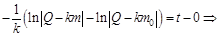

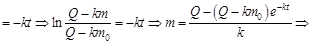
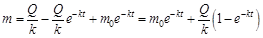 .
.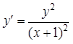 , если
, если 
 , если
, если 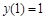
 , если
, если 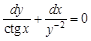 , если
, если 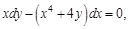 если
если 
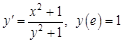 ,
, 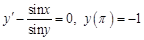

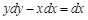 , если
, если 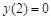
 , если
, если 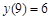
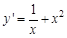 , если
, если 
 ,
, 
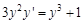 , если
, если 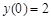
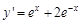 , если
, если 
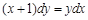 , если
, если 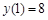
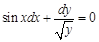 , если
, если 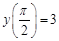
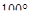 С до
С до 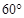 С? Температура окружающей среды поддерживается постоянной и равна
С? Температура окружающей среды поддерживается постоянной и равна 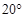 .
.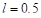 м интенсивность света убывает в два раза.
м интенсивность света убывает в два раза.


