
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра экспериментальной физикиСодержание книги
Поиск на нашем сайте Кафедра экспериментальной физики Манина Е.А., Шадрин Г.А. МАТЕМАТИКА ДЛЯ МЕДИЦИНСКИХ СПЕЦИАЛЬНОСТЕЙ Учебно-методическое пособие Сургут Издательский центр СурГУ 2019 УДК 517 + 53 ББК 22.161.1 + 22.3 М 471
Печатается по решению редакционно-издательского совета СурГУ
Рецензент к.п.н., доцент Саркисян Т.А.
Манина Е. А. М471 Математика для медицинских специальностей: учеб.-метод. пособие / Е.А. Манина, Г.А. Шадрин; Сургут. гос. ун-т. – Сургут: ИЦ СурГУ, 2019.
Учебно-методическое пособие содержит теоретический материал и указания к выполнению практических заданий по математике. Пособие предназначено для студентов медицинского института, обучающихся по направлениям 31.05.01 «Лечебное дело», 31.05.02 «Педиатрия» и изучающих дисциплину «Физика, математика». УДК 517 + 53 ББК 22.161.1 + 22.3
© Е.А. Манина, Г.А. Шадрин, 2019 © БУ ВО «Сургутский государственный университет», 2019 СОДЕРЖАНИЕ
ВВЕДЕНИЕ ПРОИЗВОДНАЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ Производные высших порядков Пусть функция В общем случае n-ой производной функции или производной n-го порядка в точке
Производные порядков выше первого называют производными высших порядков. Порядок таких производных указывают в круглых скобках, чтобы не путать их со степенями функций. Производные высших порядков можно обозначать и через дифференциалы. Например, Рассмотрим примеры нахождения производных высших порядков. Пример 1.
Видим, что эта функция имеет ненулевые производные для первых трех порядков, а производные 4-го и более высоких порядков будут равны нулю. Пример 2.
Заметим, что выражения найденных производных имеют схожие элементы, и можно записать общую формулу для определения производной n-го порядка:
Тогда сотая производная исходной функции будет равна:
Но так красиво бывает далеко не всегда. Довольно часто функция, являющаяся производной очередного порядка, становится более сложной чем та, от которой эту производную нашли. Пример 3.
Как видим, производные более высоких порядков этой функции становятся все более сложными.
1.5. Задания для самостоятельного решения I. Найдите производные функции одной переменной
II. Найдите дифференциалы функций одной переменной
III. Найдите приближенное значение функции
IV. Найдите приближенно числовое значение функции
V. Найдите производные указанных порядков для приведенных функций:
ЧАСТНЫЕ ПРОИЗВОДНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Нескольких переменных Мы уже отмечали, что реальные процессы сложны и многогранны. На их протекание влияет множество факторов, что при математическом описании отражается в зависимости функции от нескольких переменных. Но нельзя изучать влияние на функцию всех переменных одновременно. Это делают поочередно, рассматривая, как изменяется результат (функция) при изменении одного фактора (одной переменной), затем другого фактора (следующей переменной) и т.д. Одновременное же изучение зависимости функции от нескольких факторов может дать неверный результат, так как одни факторы могут усиливать друг друга, другие ослаблять или компенсировать. Поэтому и возникает задача изучения быстроты изменения результата (функции) от каждого конкретного, влияющего на нее фактора (переменной). Нахождение изменения функции в частности от данной, конкретной переменной – по сути и есть вычисление частной производной. Частной производной функции
Аналогично дают определение частной производной функции по любому другому ее аргументу, например, по
Обращаем внимание на то, что при вычислении частной производной функции по какому-либо ее аргументу, все остальные аргументы считают постоянными величинами. Фактически частную производную ищут как обыкновенную производную функции одной переменной, полагая остальные переменные константами. Выражения Рассмотрим примеры нахождения частных производных функций. Будем помнить, что те аргументы, по которым в данном случае не ищем производную, считаем константами. А все постоянные величины можно выносить за знак производной. Поэтому для того, чтобы было проще решать, сначала будем выносить все константы за знак производной, а затем искать производную от оставшегося выражения. Пример 1.
Отметим, что второе слагаемое функции
Напомним, что производную от а) представить ее как степенную функцию, стоящую в числителе б) найти производную этой функции по правилу для производной частного:
Как видим, результаты получаются одинаковые. Пример 2.
Пример 3.
Так же, как и для функций одной переменной, для функций, зависящих от нескольких переменных, можно искать производные высших порядков. Рассмотрим это на примере функции двух переменных. Частными производными второго порядка или вторыми частными производными функции Частные производные высших порядков, взятые только по одной переменной, называют чистыми производными, а те, что берут по разным переменным, называют смешанными производными. Частные производные второго порядка функции двух переменных обозначают так:
Как видим, вторые смешанные производные отличаются друг от друга порядком дифференцирования. Отметим, что существует теорема о том, что, если вторые смешанные производные функции двух переменных существуют и непрерывны в точке дифференцирования, то они равны между собой. Покажем вычисление вторых производных функции двух переменных на примере. Пример 1.
Теперь найдем вторые частные производные функции. Сначала дважды по
Теперь дважды по
А теперь найдем смешанные производные второго порядка. Сначала по
Найдем смешанную производную второго порядка по
Видим, что смешанные производные второго порядка равны. Пример 2. Найдем частные производные первого порядка.
Найдем частные производные второго порядка.
Видим, что смешанные производные второго порядка равны. Можно искать частные производные функций и более высоких порядков. Аналогично рассмотренному выше находят частные производные функций, зависящих от трех и более аргументов.
Решение интеграла по частям Метод интегрирования по частям вытекает из правил дифференцирования и свойств неопределенных интегралов. Возьмем произведение двух функций
Проинтегрируем обе части последнего равенства:
Используя свойство 2 неопределенных интегралов, имеем
Эту формулу называют формулой интегрирования по частям. Суть метода интегрирования по частям заключается в том, что часть подынтегрального выражения, не содержащую дифференциал переменной, обозначают через функцию Рассмотрим примеры интегрирования по частям. Пример 1. Введем обозначения функции
После применения формулы интегрирования по частям получили интеграл более сложный, чем исходный. Это значит, что наша замена была неудачной. Не целесообразно степенную функцию (у нас это Введем другую замену:
Пример 2.
Замена опять проведена неудачно. Опять увеличился показатель степенной функции, но, кроме этого, под интегралом осталась тригонометрическая функция. Функция Введем другую замену:
Пример 3.
Видим, что подынтегральное выражение упростилось (понизился показатель степенной функции). Чтобы совсем вывести степенную функцию из под интеграла, решим новый интеграл также по частям:
Пример 4.
Пример 5. Видим, что в этом примере под интегралом стоят функции
Теперь полученный интеграл также по частям с теми же заменами:
Объедим исходный интеграл и полученный результат:
Заметим, что в левой и правой частях этого равенства стоят одинаковые интегралы. Перенесем их в одну часть и сложим, как подобные слагаемые:
Таким образом, не имея возможности вычислить исходный интеграл, мы сумели найти, чему он будет равен.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ Учебно-методическое пособие
Редактор Верстка
Подписано в печать 00.00.2019 г. Формат 60×84/16. Усл. печ. л.3,5. Уч.-изд. л. 2,8. Тираж 90. Заказ № 00.
Оригинал-макет подготовлен и отпечатан в издательском центре СурГУ. Тел. (3462) 76-30-65, 76-30-66. (3462) 76-30-67
БУ ВО «Сургутский государственный университет» 628400, Россия, Ханты-Мансийский автономный округ, г. Сургут, пр. Ленина, 1. Тел. (3462) 76-29-00, факс (3462) 76-29-29. Кафедра экспериментальной физики Манина Е.А., Шадрин Г.А.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 423; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

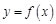 определена на некотором интервале (a, b), и пусть в каждой точке этого интервала она имеет производную
определена на некотором интервале (a, b), и пусть в каждой точке этого интервала она имеет производную 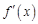 . Эту производную называют первой производной или производной первого порядка для данной функции. Эта производная сама может являться функцией
. Эту производную называют первой производной или производной первого порядка для данной функции. Эта производная сама может являться функцией 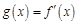 , определенной на интервале (a, b). Если функция
, определенной на интервале (a, b). Если функция 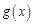 имеет на этом интервале производную в точке
имеет на этом интервале производную в точке  , то эту производную называют второй производной или производной второго порядка для функции
, то эту производную называют второй производной или производной второго порядка для функции 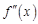 . Аналогично эта производная может являться функцией
. Аналогично эта производная может являться функцией 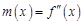 , определенной на интервале (a, b). Если и она имеет на интервале (a, b) в точке
, определенной на интервале (a, b). Если и она имеет на интервале (a, b) в точке 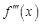 . Такие же рассуждения можно провести для производной любого порядка.
. Такие же рассуждения можно провести для производной любого порядка.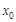 называют производную от производной (n-1)-го порядка в этой точке:
называют производную от производной (n-1)-го порядка в этой точке: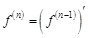 .
.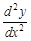 или
или 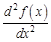 – производная второго порядка функции
– производная второго порядка функции 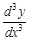 или
или 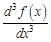 – третья производная функции
– третья производная функции 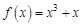 . Найдем все возможные производные высших порядков для этой функции.
. Найдем все возможные производные высших порядков для этой функции.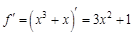
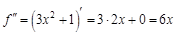
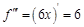
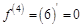
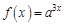 . Найдем 100-ю производную этой функции.
. Найдем 100-ю производную этой функции.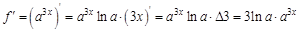
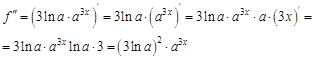
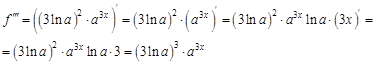
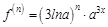 .
.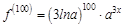 .
.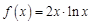 . Найдем несколько первых производных этой функции.
. Найдем несколько первых производных этой функции.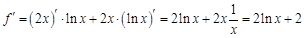
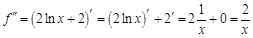
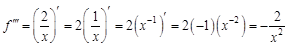
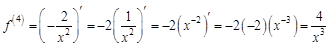
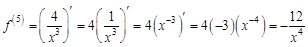
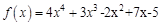
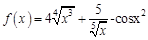
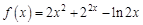
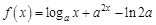
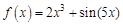
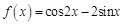
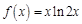
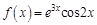
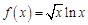
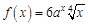
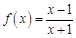
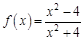
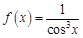
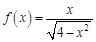
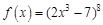
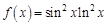
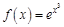
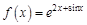
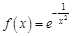
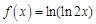
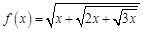
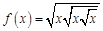
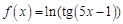
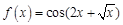
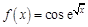
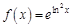
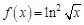
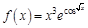
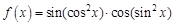
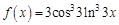
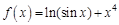
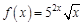
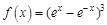
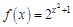
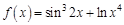
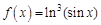
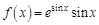
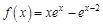
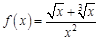
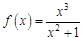
 в точке
в точке 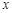 , если известно, что:
, если известно, что: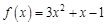 ,
,
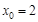 ,
,
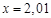
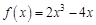 ,
,
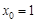 ,
,
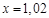
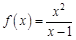 ,
,
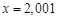
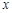 , если известно, что:
, если известно, что: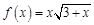 ,
,
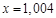
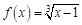 ,
,
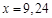
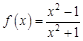 ,
,
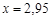
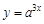
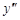
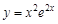
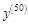
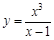
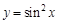
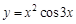
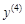
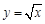
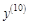
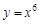
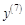
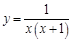
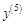
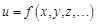 по аргументу
по аргументу 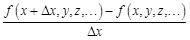 при стремлении приращения
при стремлении приращения 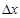 к нулю и записывают:
к нулю и записывают: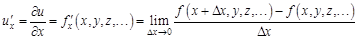 .
.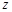 :
: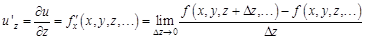 .
.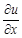 ,
, 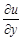 ,
, 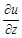 не воспринимают как отношение дифференциалов, их рассматривают как неразрывные символы частных производных.
не воспринимают как отношение дифференциалов, их рассматривают как неразрывные символы частных производных.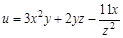 . Найдите частные производные функции
. Найдите частные производные функции 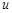 по всем ее переменным.
по всем ее переменным.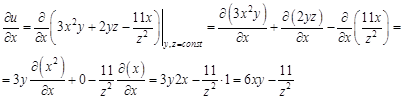
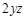 не содержит переменной
не содержит переменной 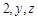 сейчас считаем константами, а производная постоянной величины равна нулю.
сейчас считаем константами, а производная постоянной величины равна нулю.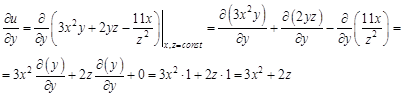
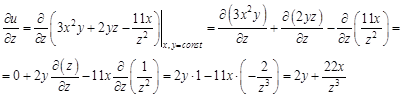
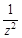 можно найти двумя способами:
можно найти двумя способами: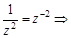
 ;
;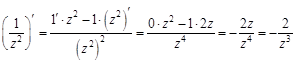 .
.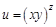 . Найдите частные производные функции
. Найдите частные производные функции 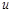 по всем ее переменным.
по всем ее переменным.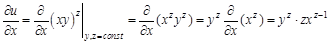
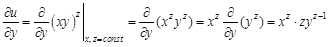
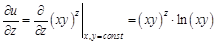
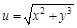 . Найдите частные производные функции
. Найдите частные производные функции 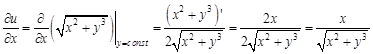
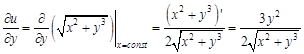
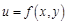 называют частные производные от частных производных этой функции первого порядка.
называют частные производные от частных производных этой функции первого порядка.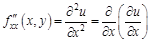 – вторая частная производная функции
– вторая частная производная функции 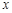 , то есть сначала взяли первую частную производную функции
, то есть сначала взяли первую частную производную функции 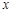 , а затем взяли частную производную по переменной
, а затем взяли частную производную по переменной 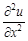 читают так «дэ два у по дэ икс дважды»; обращаем внимание, что в этой записи цифры 2 означают порядок производной (вверху) и сколько раз взята производная данной функции по переменной
читают так «дэ два у по дэ икс дважды»; обращаем внимание, что в этой записи цифры 2 означают порядок производной (вверху) и сколько раз взята производная данной функции по переменной 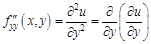 – вторая частная производная функции
– вторая частная производная функции 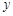 ;
;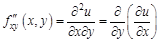 – вторая смешанная производная функции
– вторая смешанная производная функции 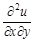 читают так «дэ два у по дэ икс дэ игрек»;
читают так «дэ два у по дэ икс дэ игрек»;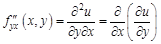 – вторая смешанная производная функции
– вторая смешанная производная функции 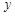 , а затем от полученной производной взяли частную производную по переменной
, а затем от полученной производной взяли частную производную по переменной 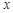 ; запись
; запись 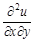 читают так «дэ два у по дэ икс дэ игрек».
читают так «дэ два у по дэ икс дэ игрек». . Найдем вторые частные производные этой функции. Для этого сначала найдем ее первые частные производные.
. Найдем вторые частные производные этой функции. Для этого сначала найдем ее первые частные производные.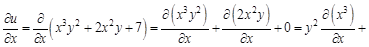
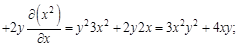
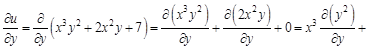
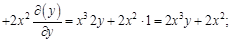
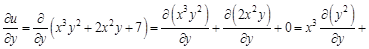
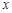 :
: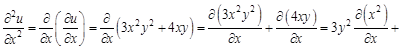
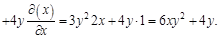
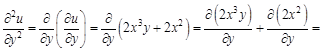
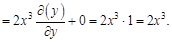
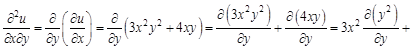
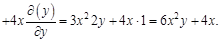
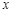 :
: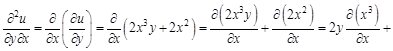
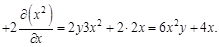
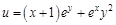 . Найти для указанной функции все частные производные второго порядка.
. Найти для указанной функции все частные производные второго порядка.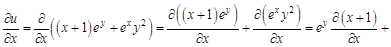
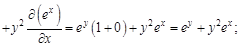
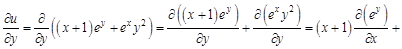
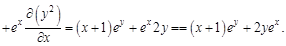
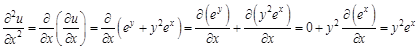
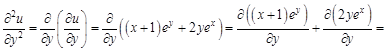
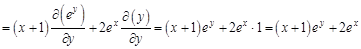
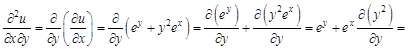
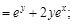
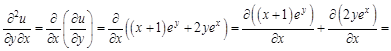
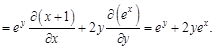
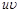 и найдем дифференциал этого произведения:
и найдем дифференциал этого произведения: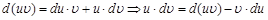
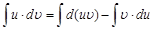
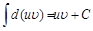 . Тогда получим:
. Тогда получим: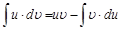
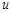 . Тогда оставшаяся часть подынтегрального выражения, в которую входит дифференциал переменной, будет
. Тогда оставшаяся часть подынтегрального выражения, в которую входит дифференциал переменной, будет 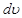 . Согласно формуле интегрирования по частям, еще потребуется найти функцию
. Согласно формуле интегрирования по частям, еще потребуется найти функцию 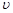 и дифференциал
и дифференциал 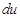 . После чего все величины подставляют, приравнивая исходный интеграл к правой части указанной формулы. При удачном выборе функции
. После чего все величины подставляют, приравнивая исходный интеграл к правой части указанной формулы. При удачном выборе функции 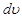 интеграл в правой части упрощается и его можно привести к табличному виду одним из описанных выше способов. Но бывают случаи, когда новый записанный интеграл правой части формулы требуется еще раз взять по частям или применить другой метод интегрирования.
интеграл в правой части упрощается и его можно привести к табличному виду одним из описанных выше способов. Но бывают случаи, когда новый записанный интеграл правой части формулы требуется еще раз взять по частям или применить другой метод интегрирования.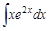
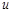 и
и 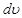 найдем соответственно
найдем соответственно 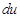 и
и 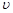 следует каждый раз осуществлять проверку, находя дифференциал от подобранной функции и сравнивая его с
следует каждый раз осуществлять проверку, находя дифференциал от подобранной функции и сравнивая его с 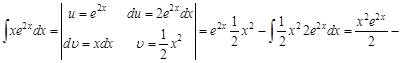
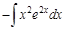 .
.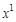 ) вводить в часть выражения, содержащую дифференциал
) вводить в часть выражения, содержащую дифференциал 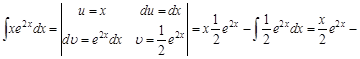
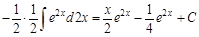 .
.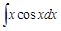
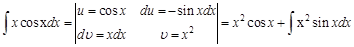 .
.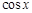 сменилась на ковариантную ей функцию
сменилась на ковариантную ей функцию 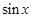 . Работая с функциями
. Работая с функциями  ,
, 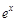 нужно смотреть, в сочетании с какими функциями они стоят в исходном интеграле, и какие замены целесообразно проводить.
нужно смотреть, в сочетании с какими функциями они стоят в исходном интеграле, и какие замены целесообразно проводить.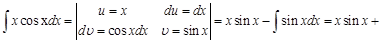
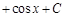
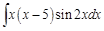
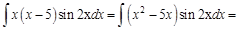
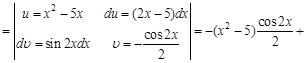
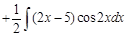
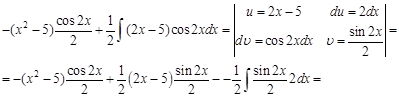
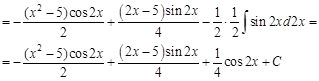
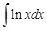
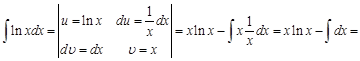
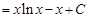
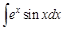
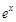 и
и 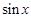 , и какую бы из них мы не обозначали через
, и какую бы из них мы не обозначали через 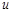 , под интегралом останется
, под интегралом останется 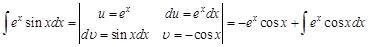 .
.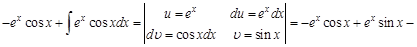
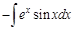 .
.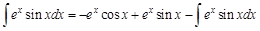 .
.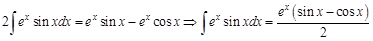 .
.


