
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка характеристик, измеренных в разных шкалахСодержание книги Поиск на нашем сайте
Теория измерений Основные понятия теории измерений Шкалы измерений Обработка характеристик, измеренных в разных шкалах Методы измерений Надежность и достоверность измерений Основные понятия теории измерений В процессе принятия решений ЛПР и эксперты формируют ситуации, цели, ограничения, варианты решений и производят измерение их характеристик. Эти измерения могут носить качественный или количественный характер и быть объективными или субъективными. Объективные измерения производятся измерительными приборами, действие которых основано на использовании физических законов. Теория объективных измерений достаточно хорошо разработана. Субъективные измерения производятся человеком, который выполняет как бы роль измерительного прибора. Естественно, что при субъективном измерении на его результаты влияет психология мышления человека. На основе использования логики и теории отношений построена теория измерений, позволяющая с единых позиций рассматривать как объективные, так и субъективные измерения. Измерение определяется как процедура сравнения объектов по определенным показателям (признакам ). В это определение включены три понятия: объекты, показатели и процедура сравнения. Объектами могут быть предметы, явления, события, решения и т.п. В качестве показателей сравнения объектов используются пространственные, временные, физические, физиологические, социологические, психологические и другие свойства и характеристики объектов. Процедура сравнения включает определение отношений между объектами и способ их сравнения. Введение конкретных показателей сравнения позволяет установить отношения между объектами, например: «больше», «меньше», «равны», «хуже», «предпочтительнее» и т.д. Существуют различные способы сравнения объектов между собой, например, последовательно с одним объектом, принимаемым за эталон, или друг с другом в некоторой последовательности. Для формального описания множества объектов и отношений между ними при фиксированных показателях сравнения вводится понятие эмпирической системы. M=<X, R>, где
Отношение является самой общей формой описания связей между объектами. Частным случаем отношения является функция. Запись вида Рассмотрим основные свойства бинарных отношений, наличие которых позволяет выделить классы отношений, широко используемых при описании взаимосвязей объектов в задаче ПР. Будем рассматривать объекты Полное и неполное отношение R может иметь следующие свойства: Ø рефлексивность Ø антирефлексивность – из Ø симметричность – если Ø антисимметричность – если одновременно Ø транзитивность – если Используя перечисленные свойства, определим отношения эквивалентности, строгого порядка и нестрогого порядка. В табл.3.4 знаком «+» указаны свойства, которыми обладают эти типы отношений. Наличие свойств непосредственно является признаком для определения типа отношения. Табл.3.4 Шкалы измерений В основе оценки лежит процесс сопоставления значений качественных или количественных характеристик исследуемой системы значениям соответствующих шкал. Тип шкалы определяется свойствами допустимого преобразования К наиболее употребимым в практике измерений типам шкал относятся: наименований; порядковая; интервалов; отношений; разностей; абсолютная. Шкала порядка Шкала называется ранговой (шкала порядка), если множество допустимых преобразований состоит из всех монотонно возрастающих допустимых преобразований шкальных значений. Следовательно, шкала порядка единственна с точностью до монотонного преобразования.
Монотонно возрастающим называется такое преобразование Измерение в шкале порядка может применяться, например, в следующих ситуациях: · необходимо упорядочить объекты во времени или пространстве. Это ситуация, когда интересуются не сравнением степени выраженности какого-либо их качества, а лишь взаимным пространственным или временным расположением этих объектов; · нужно упорядочить объекты в соответствии с каким-либо качеством, но при этом не требуется производить его точное измерение; · какое-либо качество в принципе измеримо, но в настоящий момент не может быть измерено по причинам практического или теоретического характера. Примером шкалы порядка может служить шкала твердости минералов, предложенная в 1811 г. немецким ученым Ф. Моосом и до сих пор распространенная в полевой геологической работе. Другими примерами шкал порядка могут служить шкалы силы ветра, силы землетрясения, сортности товаров в торговле, различные социологические шкалы и т.п. Любая шкала, полученная из шкалы порядка с помощью произвольного монотонно возрастающего преобразования шкальных значений, будет также точной шкалой порядка для исходной эмпирической системы с отношениями. Несколько более «сильными», чем порядковые шкалы, являются шкалы гиперпорядка. Допустимыми для этих шкал являются гипермонотонные преобразования, т.е. преобразования
только когда Таким образом, при измерении в шкалах гиперпорядка сохраняется упорядочение разностей численных оценок. Шкала интервалов Шкала интервалов применяется для отображения величины различия между свойствами объектов. Примером использования этой шкалы является измерение температуры в градусах Фаренгейта или Цельсия. При экспертном оценивании шкала интервалов применяется для оценки полезности объектов. Основным свойством шкалы интервалов является равенство интервалов. Интервальная шкала может иметь произвольные точки отсчета и масштаб. Следовательно, шкала интервалов единственна с точностью до линейного преобразования. В этой шкале отношение разности чисел в двух числовых системах определяется масштабом измерения. Одним из наиболее важных типов шкал является тип интервалов. Тип шкал интервалов содержит шкалы, единственные с точностью до множества положительных линейных допустимых преобразований вида
гдеa>0; b –любое значение. Основным свойством этих шкал является сохранение неизменными отношений интервалов в эквивалентных шкалах:
Отсюда и происходит название данного типа шкал. Примером шкал интервалов могут служить шкалы температур. В этом случае функция допустимого преобразования градусов по шкале Цельсия в градусы по шкале Фаренгейта имеет вид
и наоборот, функция допустимого преобразования градусов по шкале Фаренгейта в градусы по шкале Цельсия имеет вид
Другим примером измерения в интервальной шкале может служить признак «дата совершения события», поскольку для измерения времени в конкретной шкале необходимо фиксировать масштаб и начало отсчета. Григорианский и мусульманский календари две конкретизации шкал интервалов. Таким образом, при переходе к эквивалентным шкалам с помощью линейных преобразований в шкалах интервалов происходит изменение как начала отсчета (параметр b ), так и масштаба измерений (параметр a ). Шкалы интервалов так же, как номинальная и порядковая, сохраняют различие и упорядочение измеряемых объектов. Однако кроме этого они сохраняют и отношение расстояний между парами объектов. Запись
означает, что расстояние между В социологических исследованиях в шкалах интервалов обычно измеряют временные и пространственные характеристики объектов. Например, даты событий, стаж, возраст, время выполнения заданий, разницу в отметках на графической шкале и т.д. Однако прямое отождествление замеренных переменных с изучаемым свойством не столь просто. В качестве другого примера рассмотрим испытание умственных способностей, при котором измеряется время, требуемое для решения какой-нибудь задачи. Хотя физическое время измеряется в шкале интервалов, время, используемое как мера умственных способностей, принадлежит шкале порядка. Для того чтобы построить более совершенную шкалу, необходимо исследовать более богатую структуру этого свойства. Типичная ошибка: свойства, измеряемые в шкале интервалов, принимаются в качестве показателей для других свойств, монотонно связанных с данными. Применяемые для измерения связанных свойств исходные шкалы интервалов становятся всего лишь шкалами порядка. Игнорирование этого факта часто приводит к неверным результатам. Наиболее широко при проведении социологических измерений применяются следующие два типа интервальной шкалы. На основе шкалы Лайкерта изучается степень согласия или несогласия респондентов с определенными высказываниями. Эта шкала носит симметричный характер и измеряет интенсивность чувств респондентов. Например, содержит следующие градации: совершенно согласен (1); в какой-то мере согласен (2); отношусь нейтрально (3); в какой-то мере не согласен (4); совершенно не согласен (5). В скобках указаны баллы, приписываемые ответам на вопросы анкеты, содержащимся в определенных градациях.
С помощью шкалы Лайкерта может быть изучено мнение (отношение) сотрудников какой-то организации к различным управленческим аспектам: системе мотивации труда, психологическому климату в коллективе, к политике нововведений и др. Существуют различные варианты модификации шкалы Лайкерта, например, вводится различное число градаций (5—9). Семантическая дифференциальная шкала (семантический дифференции) содержит серию двухполярных определений, характеризующих различные свойства изучаемого объекта. Данная шкала была разработана американским ученым Ч.Осгудом для измерения смысла понятий и слов, и прежде всего для дифференциации эмоциональной стороны объекта измерения при изучении социальных установок. Таким путем определялась реакция человека в отношении изучаемого объекта. Например, при оценке морального климата в коллективе при разработке анкеты вначале выбираются характеризующие его показатели (отношения между сотрудниками, отношения между руководителями, отношения между руководителями и подчиненными и др.). Затем для каждого показателя (вопроса анкеты) составляется шкала, представляющая собой континуум образованный парой антонимичных прилагательных. Континуум содержит семь градаций интенсивности отношений. Например, по вопросу, характеризующему отношения между сотрудниками, шкала имеет следующие градации: - очень хорошие (+3); - хорошие (+2); - скорее хорошие (+1); - ни хорошие, ни плохие (0) - скорее плохие (-1); - плохие (-2); - очень плохие (-3). Каждый респондент выражает свое отношение к изучаемой проблеме по всему набору шкал. Данный тип шкалы также часто используется при определении имиджа торговой марки, магазина и т.п. Шкала отношений Шкалой отношений (подобия) называется шкала, если множество допустимых преобразований состоит из преобразований подобия
гдеа>0 –действительные числа. Нетрудно убедиться, что в шкалах отношений остаются неизменными отношения численных оценок объектов. Действительно, пусть в одной шкале объектам
Данное соотношение объясняет название шкал отношений. Примерами измерений в шкалах отношений являются измерения массы и длины объектов. Известно, что при установлении массы используется большое разнообразие численных оценок. Так, производя измерение в килограммах, получаем одно численное значение, при измерении в фунтах - другое и т.д. Однако можно заметить, что в какой бы системе единиц ни производилось измерение массы, отношение масс любых объектов одинаково и при переходе от одной числовой системы к другой, эквивалентной, не меняется. Этим же свойством обладает и измерение расстояний и длин предметов.
Как видно из рассмотренных примеров, шкалы отношений отражают отношения свойств объектов, т.е. во сколько раз свойство одного объекта превосходит это же свойство другого объекта. Шкалы отношений образуют подмножество шкал интервалов фиксированием нулевого значения параметра b: b = 0. Такая фиксация означает задание нулевой точки начала отсчета шкальных значений для всех шкал отношений. Переход от одной шкалы отношений к другой, эквивалентной ей шкале осуществляется с помощью преобразований подобия (растяжения), т.е. изменением масштаба измерений. Шкалы отношений, являясь частным случаем шкал интервалов, при выборе нулевой точки отсчета сохраняют не только отношения свойств объектов, но и отношения расстояний между парами объектов.
Шкала разностей Шкалы разностей определяются как шкалы, единственные с точностью до преобразований сдвига
b – действительные числа. Это означает, что при переходе от одной числовой системы к другой меняется лишь начало отсчета. Шкалы разностей применяются в тех случаях, когда необходимо измерить, насколько один объект превосходит по определенному свойству другой объект. В шкалах разностей неизменными остаются разности численных оценок свойств. Действительно, если
Примерами измерений в шкалах разностей могут служить измерения прироста продукции предприятий (в абсолютных единицах) в текущем году по сравнению с прошлым, увеличение численности учреждений, количество приобретенной техники за год и т.д. Другим примером измерения в шкале разностей является летоисчисление (в годах). Переход от одного летоисчисления к другому осуществляется изменением начала отсчета. Как и шкалы отношений, шкалы разностей являются частным случаем шкал интервалов, получаемых фиксированием параметра а (а= 1), т.е. выбором единицы масштаба измерений. Точка отсчета в шкалах разностей может быть произвольной Шкалы разностей, как и шкалы интервалов, сохраняют отношения интервалов между оценками пар объектов, но, в отличие от шкалы отношений, не сохраняют отношения оценок свойств объектов. Абсолютная шкала Абсолютная шкала – в которых единственными допустимыми преобразованиями являются тождественные преобразования: Абсолютные шкалы применяются, например, для измерения количества объектов, предметов, событий, решений и т.п. В качестве шкальных значений при измерении количества объектов используются натуральные числа, когда объекты представлены целыми единицами, и действительные числа, если кроме целых единиц присутствуют и части объектов. Абсолютные шкалы являются частным случаем всех ранее рассмотренных типов шкал, поэтому сохраняют любые соотношения между числами оценками измеряемых свойств объектов: различие, порядок, отношение интервалов, отношение и разность значений и т.д. Кроме указанных существуют промежуточные типы шкал, такие, например, как степенная шкала На рис.3.6 изображено соотношение между основными типами шкал в виде иерархической структуры основных шкал.
Рис.3.6. Иерархическая структура основных шкал Здесь стрелки указывают включение совокупностей допустимых преобразований более «сильных» в менее «сильные» типы шкал. При этом шкала тем «сильнее», чем меньше свободы в выборе Шкалы наименований и порядка являются качественными шкалами. В шкале наименований описывается различие или эквивалентность объектов, а в шкале порядка – качественное превосходство, отличие объектов. В этих шкалах нет понятия начала отсчета и масштаба измерения. Шкалы интервалов, отношений, разностей и абсолютная шкала являются количественными шкалами. В этих шкалах существуют понятия начала отсчета и масштаба, которые выбираются произвольно. Количественные шкалы позволяют измерить, на сколько (шкалы интервалов и разностей) или во сколько (шкалы отношений и абсолютная) раз один объект отличается от другого по выбранному показателю. Выбор той или иной шкалы для измерения определяется характером отношений между объектами эмпирической системы, наличием информации об этих отношениях и целями принятия решения. Применение количественных шкал требует значительно более полной информации об объектах по сравнению с применением качественных шкал. Следует обратить внимание на правильное согласование выбираемой шкалы измерения с целями решения. Например, если целью решения является упорядочение объектов, то нет необходимости измерять количественные характеристики объектов, достаточно определить только качественные характеристики. Типичным примером такого решения является подведение определение наилучших предприятий. Для решения этой задачи, как правило, не требуется определять, на сколько или во сколько раз один объект лучше другого, т.е. нет необходимости при таком измерении пользоваться количественными шкалами. Пример балльной оценки свойств систем
По фактическому качеству лучшей является система А, а по результатам экспертизы –Б. Таким образом, способы измерения и обработки результатов оказывают существенное влияние на результаты. Избежать ошибок можно, используя результаты, полученные в теории шкалирования, они определяют правила и перечень допустимых операций осреднения характеристик. Остановимся подробнее на правилах осреднения. Проводить осреднение допускается только для однородных характеристик, измеренных в одной шкале. Это означает, например, что не имеет физического смысла вычисление среднего значения скорости для мобильного абонентского пункта, если слагаемыми являются скорость передачи данных и скорость перемещения этого объекта. Иными словами, осредняются только такие значения Каждое значение показателя Для получения осредненного значения показателя наиболее часто применяют основные формулы осреднения (табл. 3.6). Таблица 3.6 Методы измерений Существуют прямые и косвенные процедуры измерения. В первом случае проводится непосредственное прямое оценивание измеряемого объекта (свойства). Во втором случае оценка приписывается по измеряемому признаку на основе совокупности косвенных ответов. При использовании прямого измерения некоторым индивидуумом осуществляется непосредственная оценка какого-то признака путем, как правило, выбора одного числового балла из некоторой совокупности чисел или путем выбора одного ответа из серии предложенных. В данном случае часто обращаются к респондентам с закрытыми вопросами типа: «Как часто Вы читаете какой-то специализированный журнал?» Вариантами ответов могут быть: «постоянно», «довольно часто», «редко», «никогда». Ответам могут быть приписаны числовые оценки (баллы), например соответственно 4, 3, 2, 1. Для оценки измеряемого качества иногда пользуются графическими шкалами, разделенными на равные части и снабженными словесными или числовыми обозначениями. Респондента просят сделать отметку на шкале в соответствии с его оценкой данного качества. Непосредственные оценки рассмотренного типа производятся в шкале интервалов. В шкале отношений производятся непосредственные измерения, например, возраста или показателей, основанных на денежных единицах. К наиболее употребительным методам субъективных измерений относятся: · ранжирование, · парное сравнение, · непосредственная оценка; · последовательное сравнение. При описании каждого из перечисленных методов будет предполагаться, что имеется конечное число измеряемых объектов 1) построение отношений между объектами эмпирической системы; 2) выбор отображающей функции f; 3) определение типа шкалы измерений. Ранжирование представляет собой процедуру упорядочения объектов, выполняемую ЛПР или экспертом. На основе знаний и опыта ЛПР или эксперт располагает объекты в порядке предпочтения, руководствуясь одним или несколькими выбранными показателями сравнения. В зависимости от вида отношений между объектами возможны различные варианты упорядочения объектов. Рассмотрим эти варианты. Пусть среди объектов нет одинаковых по сравниваемым показателям, т.е. нет эквивалентных объектов. В этом случае между объектами существует только отношение строгого порядка. В результате сравнения всех объектов по отношению строгого порядка составляется упорядоченная последовательность
где объект с первым номером является наиболее предпочтительным из всех объектов, объект со вторым номером менее предпочтителен первому объекту, но предпочтительнее всех остальных объектов, и т. д. Полученная система объектов с отношением строгого порядка при условии сравнимости всех объектов по этому отношению образует полный строгий порядок. Для этого отношения доказано существование числовой системы, элементами которой являются действительные числа, связанные между собой отношением неравенства. Это означает, что упорядочению объектов (4.3) соответствует упорядочение чисел
где
в которой наиболее предпочтительному объекту приписывается наименьшее число и по мере убывания предпочтения в (2.3) объектам приписываются большие числа. Соответствие последовательностей (3.1) и (3.2) или (3.1) и (3.3), т.е. их изоморфизм или гомоморфизм, можно осуществить, выбирая любые числовые представления. Единственным ограничением является монотонность преобразования. Следовательно, допустимое преобразование при переходе, от одного числового представления к другому должно обладать свойством монотонности. Но таким свойством допустимого преобразования обладает шкала порядков, поэтому ранжирование объектов есть измерение в порядковой шкале. В практике ранжирования чаше всего применяется числовое представление последовательности (1) в виде натуральных чисел
Числа
Для эквивалентных объектов удобно с точки зрения технологии последующей обработки оценок назначать одинаковые ранги, равные среднему арифметическому значению рангов, присваиваемых одинаковым объектам. Такие ранги называют связанными. Например, для (3.4) Напомним, что ранги объектов определяют только порядок расположения объектов. Ранги как числа не дают возможности сделать вывод о том, на сколько или во сколько раз предпочтительнее один объект по сравнению с другим. Если, например, ранг объекта равен трем, то отсюда не следует делать вывод о том, что объект, имеющий ранг, равный единице, в три раза предпочтительнее, чем объект, имеющий ранг, равный трем. Достоинством ранжирования как метода субъективного измерения является простота осуществления процедур, не требующая какого-либо трудоемкого обучения экспертов. Недостатком ранжирования является практическая невозможность упорядочения большого числа объектов. Как показывает опыт, при числе объектов, большем 15–20 эксперты затрудняются в построении ранжировки. Это объясняется тем, что в процессе ранжирования эксперт должен установить взаимосвязь между всеми объектами, рассматривая их как единую совокупность. При увеличении числа объектов количество связей между ними растет пропорционально квадрату числа объектов. Сохранение в памяти и анализ большой совокупности взаимосвязей между объектами ограничиваются психологическими возможностями человека. Поэтому при ранжировании большого числа объектов эксперты могут допускать существенные ошибки Парное сравнение представляет собой процедуру установления предпочтения объектов при сравнении всех возможных их пар. По сравнению с ранжированием парное сравнение представляет собой более простую задачу. При сравнении пары объектов возможно либо отношение строгого порядка, либо отношение эквивалентности. Отсюда следует, что парное сравнение есть измерение в порядковой шкале. В практике парного сравнения используются следующие числовые представления:
В табл.3.8 и 3.9 на диагонали всегда будут располагаться 1, т.к. объект всегда эквивалентен себе. Табл.3.8 Табл.3.9 Проверка правильности шкалы · отсутствие разброса ответов по значениям шкалы. Попадание ответов в один пункт свидетельствует о полной непригодности измерительного инструмента — шкалы. Такая ситуация может возникнуть или из-за «нормативного» давления в сторону общепринятого мнения, или из-за того, что градации (значения) шкалы не имеют отношения к распределению данного свойства у рассматриваемых объектов (нерелевантны). Например, при опросе все ответы концентрируются в позитивном или только в негативном конце шкалы. Конечно, это может быть и результатом единодушия оценок, но может быть и результатом того, что сама шкала неудачна, например, содержит какой-то пункт, сформулированный с сильным нормативным давлением на опрашиваемых. Допустим, задан вопрос об употреблении алкоголя и крайне негативный вариант ответа звучит так: «Я пью систематически и обычно до бесчувственного состояния». Сомнительно, чтобы даже заведомый алкоголик отметил такой пункт как показатель своего отношения к спиртному. Скорее всего, он выберет суждение с менее неприятным оттенком, например: «Я выпиваю довольно часто». Крайне отрицательный пункт шкалы здесь «не работает», он отпугивает. Вследствие этого шкала спроектирована неправильно. Другой пример. Если все опрашиваемые респонденты согласны с утверждением: «хорошо, когда используется эффективная система мотивации труда», нет ни одного ответа «не согласен», то подобная шкала не поможет дифференцировать отношение респондентов к разным методам мотивации труда. · использование части шкалы. Довольно часто обнаруживается, что практически работает лишь какая-то часть шкалы, какой-то один из ее полюсов с прилегающей более или менее обширной зоной. Так, если респондентам для оценки предлагается шкала, имеющая положительный и отрицательный полюса, в частности от +3 до —3, то при оценивании какой-то заведомо положительной ситуации респонденты не используют отрицательные оценки, а дифференцируют свое мнение лишь с помощью положительных. · неравномерное использование отдельных пунктов шкалы. Случается, что некоторое значение признака систематически выпадает из поля зрения респондентов, хотя соседние градации, характеризующие более низкую и более высокую степень выраженности признака, имеют существенное наполнение. Так, если конфигурация распределения ответов на вопрос с четырьмя упорядоченными градациями такая, как на рис.3.9, градации данной шкалы, видимо, неудачно сформулированы. Значительное наполнение двух соседних по отношению к пункту 2 пунктов (1 и 3) свидетельствует о «захвате» части голосов из плохо сформулированного пункта 2.
Рис.3.9. Пример неравномерного распределения ответов по шкале
Аналогичная картина наблюдается и в том случае, когда респонденту предлагают шкалу, имеющую слишком большую дробность: будучи не в состоянии оперировать всеми градациями шкалы, респондент выбирает лишь несколько базовых. Например, зачастую десятибалльную шкалу респонденты расценивают как некоторую модификацию пятибалльной, предполагая, что «десять» соответствует «пяти», «восемь» — «четырем», «пять» — «трем» и т.д. При этом базовые оценки используются значительно чаще, чем другие. В процессе измерения иногда возникают грубые ошибки, причиной которых могут быть неправильные записи исходных данных, плохие расчеты, неквалифицированное использование измерительных средств и т. п. Это проявляется в том, что в рядах измерений попадаются данные, резко отличающиеся от совокупности всех остальных значений. Чтобы выяснить, нужно ли эти значения признать грубыми ошибками, устанавливают критическую границу так, чтобы вероятность того, что крайние значения превысят ее, была бы достаточно малой и соответствовала бы некоторому уровню значимости а.. Это правило основано на том, что появление в ответах чрезмерно больших значений хотя и возможно, как следствие естественной вариабельности значений, но маловероятно. Если окажется, что какие-то крайние значения совокупност
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1012; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.191.148 (0.018 с.) |

 – множество объектов, в качестве которых могут рассматриваться, например, ситуация, цели, решения и т.п.;
– множество объектов, в качестве которых могут рассматриваться, например, ситуация, цели, решения и т.п.; – множество отношений между объектами.
– множество отношений между объектами. или
или  означает, что объекты
означает, что объекты  и
и  находятся между собой в отношении
находятся между собой в отношении  . Такое отношение называется бинарным (двухместным), поскольку оно связывает между собой два объекта. Если отношение имеет место одновременно между тремя объектами, то оно называется тернарным (трехместным).
. Такое отношение называется бинарным (двухместным), поскольку оно связывает между собой два объекта. Если отношение имеет место одновременно между тремя объектами, то оно называется тернарным (трехместным).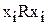 , т.е. это свойство означает, что объект находится в отношении R к самому себе;
, т.е. это свойство означает, что объект находится в отношении R к самому себе;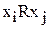 следует, что
следует, что  , т.е. свойство антирефлексивности может выполняться только для несовпадающих объектов;
, т.е. свойство антирефлексивности может выполняться только для несовпадающих объектов; , то и
, то и  , т.е. отношение симметрично к обоим объектам;
, т.е. отношение симметрично к обоим объектам; , то это означает, что
, то это означает, что  ;
; , то
, то  .
. .
. , которое удовлетворяет условию: если
, которое удовлетворяет условию: если  , то и
, то и  для любых шкальных значений
для любых шкальных значений  из области определения
из области определения  :
:
 .
. ,
,
 ,
, .
.
 и
и  в К раз больше расстояния между х3 и х4 и в любой эквивалентной шкале это значение (отношение разностей численных оценок) сохранится. При этом отношения самих оценок не сохраняются.
в К раз больше расстояния между х3 и х4 и в любой эквивалентной шкале это значение (отношение разностей численных оценок) сохранится. При этом отношения самих оценок не сохраняются.
 и
и  соответствуют шкальные значения
соответствуют шкальные значения  и
и  . Тогда имеем:
. Тогда имеем:
 ,
, в одной шкале, а
в одной шкале, а  и
и  - в другой шкале, то имеем:
- в другой шкале, то имеем:
 . Это означает, что существует только одно отображение эмпирических объектов в числовую систему. Отсюда и название шкалы, так как для нее единственность измерения понимается в буквальном абсолютном смысле.
. Это означает, что существует только одно отображение эмпирических объектов в числовую систему. Отсюда и название шкалы, так как для нее единственность измерения понимается в буквальном абсолютном смысле. (
( ) и ее разновидность логарифмическая шкала
) и ее разновидность логарифмическая шкала  (
(
 ).
).

 , которые представляют собой или оценки различных измерений одной и той же характеристики, или оценки нескольких различных однородных характеристик.
, которые представляют собой или оценки различных измерений одной и той же характеристики, или оценки нескольких различных однородных характеристик. может иметь для исследователя различную ценность, которую учитывают с помощью коэффициентов значимости
может иметь для исследователя различную ценность, которую учитывают с помощью коэффициентов значимости  причем
причем  .
. (3.1),
(3.1), , (3.2)
, (3.2) . Возможна и обратная последовательность
. Возможна и обратная последовательность , (3.3)
, (3.3) ,
,  , …,
, …,  .
. ,
,  ,…,
,…,  называются рангами и обычно обозначаются буквами
называются рангами и обычно обозначаются буквами  ,
,  ,…,
,…,  . Возможно при ранжировании получить упорядочение, соответствующее отношению нестрогого порядка
. Возможно при ранжировании получить упорядочение, соответствующее отношению нестрогого порядка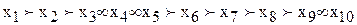 (3.4)
(3.4) и
и  .
.





