
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные типы отношений и их свойстваСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Отношение эквивалентности называется рефлексивное симметричное и транзитивное отношение и содержательно интерпретируется как взаимозаменяемость, одинаковость объектов. Для обозначения отношения эквивалентности используется специальный символ «¥». Запись Отношение строгого порядка является антирефлексивным и транзитивным отношением и может интерпретироваться как предпочтительность в широком смысле одного объекта по сравнению с другим объектом, например «важнее», «лучше», «выше», «больше» и т. п. Для обозначения отношения строгого порядка используется специальный символ « Отношение нестрогого порядка есть объединение отношений строгого порядка и эквивалентности и обладает свойствами рефлексивности, антисимметричности и транзитивности. В соответствии с этим для обозначения этого отношения применяется символ « Разнообразие возможных объектов, показателей сравнения и видов отношений, встречающихся в реальных измерениях, привело к необходимости установления универсальной системы с отношениями. В качестве такой системы используется числовая система N=<C,S>, где С – множество действительных чисел; Числовая система называется полной, если С есть множество всех действительных чисел. Отношениям строгого и нестрогого порядка между объектами соответствуют отношения строгого и нестрогого неравенства между числами. Числовая система используется для унификации процесса измерения. Измерение заключается в отображении объектов эмпирической системы на множество чисел таким образом, чтобы отношения между числами, отображающими объекты, сохраняли отношения между самими объектами. Для того чтобы числовая система сохраняла свойства и отношения объектов, необходимо, чтобы она была изоморфной или по крайней мере гомоморфной эмпирической системе. Числовая система изоморфна эмпирической системе, если они подобны и между ними существует взаимно однозначное отображение (функция) f объектов на множество чисел, такое, что отношение R между объектами имеет место тогда и только тогда, когда имеет место отношение между числами, отображающими объекты на числовой оси. Подобие двух систем с отношениями означает, что количество отношений и их местность в обеих системах одинаково. Условие взаимной однозначности отображения f является в ряде случаев слишком жестким и не всегда необходимым. Если устранить это условие из предыдущего определения изоморфизма, то приходим к понятию гомоморфизма. Таким образом, измерение представляет собой отображение объектов эмпирической системы на множество чисел в числовой системе. Схематически это представляется следующим образом
С помощью отображения (функции) f каждому объекту эмпирической системы приписывается число Основными проблемами теории измерений являются проблемы представления и единственности. Проблема представления заключается в доказательстве возможности представления эмпирической системы с помощью числовой системы, сохраняющей отношения между объектами, т.е. гомоморфной или изоморфной. В теории измерений доказано существование числовых систем для описания множества объектов, связанных отношениями эквивалентности, строгого и нестрогого порядков. Проблема единственности заключается в определении всех возможных способов представления заданной эмпирической системы различными числовыми системами и установления связи между ними. Проблему единственности можно сформулировать как проблему определения типа шкалы. Шкалой называется совокупность эмпирической системы М, числовой системы N и отображения f:
Пусть отображениями
С помощью функции допустимого преобразования можно описать связь между любыми числовыми системами, выбираемыми для отображения одной и той же эмпирической системы. Например, одна и та же температура Шкалы измерений В основе оценки лежит процесс сопоставления значений качественных или количественных характеристик исследуемой системы значениям соответствующих шкал. Тип шкалы определяется свойствами допустимого преобразования К наиболее употребимым в практике измерений типам шкал относятся: наименований; порядковая; интервалов; отношений; разностей; абсолютная.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.253.73 (0.006 с.) |

 ¥
¥  означает эквивалентность объектов. Отношение эквивалентности порождает разбиение множества объектов на классы. В каждый класс попадают эквивалентные, т.е. неразличимые по показателю (или группе показателей), объекты.
означает эквивалентность объектов. Отношение эквивалентности порождает разбиение множества объектов на классы. В каждый класс попадают эквивалентные, т.е. неразличимые по показателю (или группе показателей), объекты. », например если объект
», например если объект  . Отношение полного строгого порядка порождает строгое упорядочение объектов по предпочтительности.
. Отношение полного строгого порядка порождает строгое упорядочение объектов по предпочтительности. ». Запись
». Запись  означает, что объект
означает, что объект  – множество отношений между числами.
– множество отношений между числами.
 . При таком отображении отношения между числами должны сохранять отношения между объектами, т.е. если
. При таком отображении отношения между числами должны сохранять отношения между объектами, т.е. если  .
.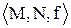 .
.  и
и  – две шкалы, различающиеся отображениями
– две шкалы, различающиеся отображениями 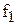 и
и  , тогда возникает вопрос о взаимосвязи числовых значений, полученных при отображении одного и того же объекта. Пусть
, тогда возникает вопрос о взаимосвязи числовых значений, полученных при отображении одного и того же объекта. Пусть 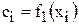 и
и  , где
, где  и
и  – разные числа. Тогда связь между числами
– разные числа. Тогда связь между числами  :
: .
.


