
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные формулы осреднения показателейСодержание книги Поиск на нашем сайте
Простая и взвешенные средние величины различаются не только по величине (не всегда), по способу вычисления, но и по своей роли в решении задач системного анализа. При этом средневзвешенные величины используются для сравнения систем с учетом вклада различных факторов в осредненную оценку. Рассмотрим, например, среднее количество информации, получаемой из сети Интернет организацией, пользующейся услугами различных прикладных служб. Если эта средняя величина входит в систему показателей себестоимости, протоколов работы, типов используемых линий, то следует применять взвешенное среднее, так как произведение невзвешенного среднего на общую пропускную способность линий не даст количества полученной информации, поскольку служба электронной почты используется, например, значительно реже, чем WWW, и, следовательно, вносит меньший вклад в общее количество получаемой информации. Если же необходимо изучить связь количества получаемой информации с днем недели, то следует применять простое среднее количество информации за сутки, полностью абстрагируясь от различий между типами служб. Среднеарифметическое используется в случаях, когда важно сравнить абсолютные значения какой-либо характеристики нескольких систем. Например, скорость вывода на печать текстов (лист/мин) для различных печатающих устройств. Если при замене индивидуальных значений показателя на среднюю величину требуется сохранить неизменной сумму квадратов исходных величин (измерение вариации характеристики в совокупности), то в качестве средней следует использовать среднеквадратичное. Например, при определении местоположения источника радиоизлучения в радиоразведке вычисляется среднеквадратичное отклонение нескольких измерений. Среднегеометрическое, в свою очередь, используется для определения относительной разности отдельных значений при необходимости сохранения произведения индивидуальных величин тогда, когда среднее значение качественно одинаково удалено от максимального и минимального значений, т.е. когда важны не абсолютные значения, а относительный разброс характеристик. В статистике среднегеометрическое находит применение при определении средних темпов роста.
Например, если максимальная производительность процессора на операциях с данными целочисленного типа составляет для сжатия текстового файла миллион условных единиц, а для сжатия изображений графических объектов сто, то какую величину считать средней? Среднеарифметическое (500 000) качественно однородно с максимальным и резко отлично от минимального. Среднегеометрическое по логике дает верный ответ: 10 000. Не миллион, и не сотня, а нечто среднее. Среднегармоническое используется, если необходимо, чтобы неизменной оставалась сумма величин, обратных индивидуальным значениям характеристик. Пусть, например, в режиме обмена данными средняя скорость передачи данных по прямому каналу составляет 64 Кбайт/с, а средняя скорость по обратному каналу 2,4 Кбайт/с. Какова средняя скорость обмена данными? При замене индивидуальных значений скорости у1 = 64 и у2 = 2,4 на среднюю величину необходимо, чтобы неизменной величиной осталось время передачи в обе стороны, иначе средняя скорость может оказаться любой. Таким образом, v = 2(1/64+1/2,4)-1 Приведенные примеры показывают, что в каждом конкретном случае требуется четкое определение допустимых условий применения средних величин. Соотношение между разными типами средних величин определяется правилом мажорантности средних СГр < СГм < СА < СК. Использование необоснованных способов определения средних величин может привести к искусственному завышению или занижению осредненного значения показателя качества системы. Сводные данные по характеристикам разных шкал и перечень допустимых операций осреднения характеристик приведены в табл.3.7, откуда следует, что для величин, измеренных в номинальной шкале, никаких осреднений производить не допускается. Среднеарифметическое применимо для величин, измеренных в шкалах интервалов, разностей, отношений и абсолютной, но недопустимо для шкалы порядка. Более устойчивой оценкой среднего является медиана (50-процентный квантиль), которая рекомендуется как основной показатель для шкал порядка, интервалов, разностей, отношений и абсолютной. Математическое ожидание допустимо для шкал интервалов, разностей, отношений и абсолютных, но не столь устойчиво, как медиана. Применение математического ожидания для величин, измеренных в шкале порядка, является некорректным. Среднегеометрическое является единственно допустимым средним для степенных и логарифмических шкал, а также одним из допустимых для шкалы отношений. Для шкалы отношений допустимы также средневзвешенное арифметическое, среднегармоническое и среднеквадратичное.
Вопрос о применении средних в настоящее время исследован достаточно полно. Этого нельзя сказать о средневзвешенных. Однако для наиболее часто применяемого средневзвешенного арифметического доказан следующий факт. Средневзвешенное арифметическое, часто применяемое как обобщенный линейный критерий (аддитивная свертка при сведении векторной задачи к скалярной, при осреднении показателей и др.), допустимо использовать тогда и только тогда, когда значения частных показателей можно представить мультипликативным метризованным отношением линейного порядка или, другими словами, когда они измерены в шкале отношений. Доказано, что задача линейного программирования корректна, если коэффициенты ее целевой функции и ограничений измерены в шкале отношений.
Будущее развития теории шкалирования и ее применения для нужд математического обеспечения ИС связаны с дальнейшим развитием понятия измерения. Одним из направлений расширения понимания шкалы является привлечение понятий нечеткой и лингвистических переменных, используемых в теории нечетких множеств. Использование понятия функции принадлежности Например, пусть рассматриваемое нечеткое множество возраст людей. Нечеткими переменными (шкальными значениями), означающими возраст, являются лингвистические переменные «молодой», «средний», «старый» с приписанными им функциями принадлежности, которые можно определить так, как показано на рис.3.7. При этом 20-летний человек относится к нечеткому подмножеству возраста «молодой» с функцией принадлежностью
Рис.3.7. Пример нечеткой шкалы Методы измерений Существуют прямые и косвенные процедуры измерения. В первом случае проводится непосредственное прямое оценивание измеряемого объекта (свойства). Во втором случае оценка приписывается по измеряемому признаку на основе совокупности косвенных ответов. При использовании прямого измерения некоторым индивидуумом осуществляется непосредственная оценка какого-то признака путем, как правило, выбора одного числового балла из некоторой совокупности чисел или путем выбора одного ответа из серии предложенных. В данном случае часто обращаются к респондентам с закрытыми вопросами типа: «Как часто Вы читаете какой-то специализированный журнал?» Вариантами ответов могут быть: «постоянно», «довольно часто», «редко», «никогда». Ответам могут быть приписаны числовые оценки (баллы), например соответственно 4, 3, 2, 1. Для оценки измеряемого качества иногда пользуются графическими шкалами, разделенными на равные части и снабженными словесными или числовыми обозначениями. Респондента просят сделать отметку на шкале в соответствии с его оценкой данного качества.
Непосредственные оценки рассмотренного типа производятся в шкале интервалов. В шкале отношений производятся непосредственные измерения, например, возраста или показателей, основанных на денежных единицах. К наиболее употребительным методам субъективных измерений относятся: · ранжирование, · парное сравнение, · непосредственная оценка; · последовательное сравнение. При описании каждого из перечисленных методов будет предполагаться, что имеется конечное число измеряемых объектов 1) построение отношений между объектами эмпирической системы; 2) выбор отображающей функции f; 3) определение типа шкалы измерений. Ранжирование представляет собой процедуру упорядочения объектов, выполняемую ЛПР или экспертом. На основе знаний и опыта ЛПР или эксперт располагает объекты в порядке предпочтения, руководствуясь одним или несколькими выбранными показателями сравнения. В зависимости от вида отношений между объектами возможны различные варианты упорядочения объектов. Рассмотрим эти варианты. Пусть среди объектов нет одинаковых по сравниваемым показателям, т.е. нет эквивалентных объектов. В этом случае между объектами существует только отношение строгого порядка. В результате сравнения всех объектов по отношению строгого порядка составляется упорядоченная последовательность
где объект с первым номером является наиболее предпочтительным из всех объектов, объект со вторым номером менее предпочтителен первому объекту, но предпочтительнее всех остальных объектов, и т. д. Полученная система объектов с отношением строгого порядка при условии сравнимости всех объектов по этому отношению образует полный строгий порядок. Для этого отношения доказано существование числовой системы, элементами которой являются действительные числа, связанные между собой отношением неравенства. Это означает, что упорядочению объектов (4.3) соответствует упорядочение чисел
где
в которой наиболее предпочтительному объекту приписывается наименьшее число и по мере убывания предпочтения в (2.3) объектам приписываются большие числа. Соответствие последовательностей (3.1) и (3.2) или (3.1) и (3.3), т.е. их изоморфизм или гомоморфизм, можно осуществить, выбирая любые числовые представления. Единственным ограничением является монотонность преобразования. Следовательно, допустимое преобразование при переходе, от одного числового представления к другому должно обладать свойством монотонности. Но таким свойством допустимого преобразования обладает шкала порядков, поэтому ранжирование объектов есть измерение в порядковой шкале. В практике ранжирования чаше всего применяется числовое представление последовательности (1) в виде натуральных чисел
Числа
Для эквивалентных объектов удобно с точки зрения технологии последующей обработки оценок назначать одинаковые ранги, равные среднему арифметическому значению рангов, присваиваемых одинаковым объектам. Такие ранги называют связанными. Например, для (3.4) Напомним, что ранги объектов определяют только порядок расположения объектов. Ранги как числа не дают возможности сделать вывод о том, на сколько или во сколько раз предпочтительнее один объект по сравнению с другим. Если, например, ранг объекта равен трем, то отсюда не следует делать вывод о том, что объект, имеющий ранг, равный единице, в три раза предпочтительнее, чем объект, имеющий ранг, равный трем. Достоинством ранжирования как метода субъективного измерения является простота осуществления процедур, не требующая какого-либо трудоемкого обучения экспертов. Недостатком ранжирования является практическая невозможность упорядочения большого числа объектов. Как показывает опыт, при числе объектов, большем 15–20 эксперты затрудняются в построении ранжировки. Это объясняется тем, что в процессе ранжирования эксперт должен установить взаимосвязь между всеми объектами, рассматривая их как единую совокупность. При увеличении числа объектов количество связей между ними растет пропорционально квадрату числа объектов. Сохранение в памяти и анализ большой совокупности взаимосвязей между объектами ограничиваются психологическими возможностями человека. Поэтому при ранжировании большого числа объектов эксперты могут допускать существенные ошибки Парное сравнение представляет собой процедуру установления предпочтения объектов при сравнении всех возможных их пар. По сравнению с ранжированием парное сравнение представляет собой более простую задачу. При сравнении пары объектов возможно либо отношение строгого порядка, либо отношение эквивалентности. Отсюда следует, что парное сравнение есть измерение в порядковой шкале. В практике парного сравнения используются следующие числовые представления:
В табл.3.8 и 3.9 на диагонали всегда будут располагаться 1, т.к. объект всегда эквивалентен себе. Табл.3.8 Табл.3.9
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.64.124 (0.012 с.) |


 4,8 Кбайт/с.
4,8 Кбайт/с.
 , используемой в этой теории, создает базу для введения более тонкой структуры измерения качественных характеристик и учета неопределенностей, свойственных сложным системам, на основе понятия нечеткой шкалы.
, используемой в этой теории, создает базу для введения более тонкой структуры измерения качественных характеристик и учета неопределенностей, свойственных сложным системам, на основе понятия нечеткой шкалы. , и он же с функцией принадлежности
, и он же с функцией принадлежности  относится к нечеткому подмножеству возраста средний (см. рис.3.7)
относится к нечеткому подмножеству возраста средний (см. рис.3.7)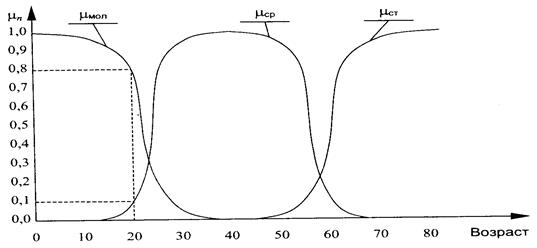
 и сформулирован один или несколько признаков сравнения, по которым осуществляется сравнение свойств объектов. Следовательно, методы измерения будут различаться лишь процедурой сравнения объектов. Процедура сравнения включает:
и сформулирован один или несколько признаков сравнения, по которым осуществляется сравнение свойств объектов. Следовательно, методы измерения будут различаться лишь процедурой сравнения объектов. Процедура сравнения включает: (3.1),
(3.1), , (3.2)
, (3.2) . Возможна и обратная последовательность
. Возможна и обратная последовательность , (3.3)
, (3.3) ,
,  , …,
, …,  .
. ,
,  ,…,
,…,  называются рангами и обычно обозначаются буквами
называются рангами и обычно обозначаются буквами  ,
,  ,…,
,…,  . Возможно при ранжировании получить упорядочение, соответствующее отношению нестрогого порядка
. Возможно при ранжировании получить упорядочение, соответствующее отношению нестрогого порядка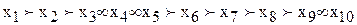 (3.4)
(3.4) и
и  .
.




