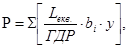Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формули для розрахунків забруднення атмосферного повітряСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Забруднення атмосферного повітря здійснюється однією речовиною. В цьому випадку порівняння ступеня забруднення атмосферного повітря в зонах спостереження проводять за середньомісячними концентраціями з ймовірністю 98%. Для цього спочатку вираховують середньомісячну концентрацію забруднювача за формулою:
де С1, С2, Сn – концентрації за даними аналізу; n - кількість аналізів за місяць.
Для розрахунку слід використовувати максимально разові або середньодобові концентрації, виключаючи з розрахунків «крайні» значення результатів аналізу. Далі розраховують середньо квадратичне відхилення
та коефіцієнт варіації (Сv)
Знаючи коефіцієнт варіації (Сv) за графіком визначають значення коефіцієнту (а), який необхідний для розрахунку середньомісячної концентрації См з ймовірністю 98% за формулою: См= а × С
Саме по значенню середньомісячної концентрації См і співставляють рівні забруднення атмосферного повітря в зонах спостереження. 2. При наявності в атмосферному повітрі кількох речовин, які не мають ефекту біологічної сумації, розраховують сумарний показник забруднення атмосферного повітря (Ксум) за формулою:
де: См1, Смn - концентрації окремих забруднювачів, мг/м3; Смі – інтегрована (узагальнена) середньомісячна концентрація усіх забруднювачів, мг/м3; ГДК1, ГДКn - гранично допустимі концентрації забруднювачів, мг/м3; М - коефіцієнт, величина якого залежить від класу небезпеки забруднювача: І клас (А) – надзвичайно небезпечні, М = 1,0; ІІ клас (Б) – високонебезпечні, М = 1,5; ІІІ клас (В) – помірно небезпечі, М = 2,0; ІV клас (Г) – малонебезпечні, М = 4,0.
3. При наявності в атмосферному повітрі кількох речовин, які мають ефект біологічної сумації, розраховують приведену концентрацію (Смприв) за формулою:
де См1 - концентрація речовини, на яку проводиться сумація, мг/м3; См2, Смn - концентрація забруднювачів, мг/м3; ГДК1 - гранично допустима концентрація речовини, на яку проводиться сумація, мг/м3; ГДК2, ГДКn - гранично допустимі концентрації інших забруднювачів, мг/м3.
4. При наявності в атмосферному повітрі речовин, які мають ефект біологічної сумації та речовин, які не мають ефекту біологічної сумації, розраховують сумарний показник забруднення (Ксум) за формулою:
де Смприв – приведена концентрація, мг/м3; ГДКприв – гранично допустима концентрація речовини, на яку проводять сумацію, мг/м3.
5. Ступінь забруднення атмосферного повітря в балах розраховують за формулою:
де А,Б,В,Г – класи небезпеки речовин; 1,2…n – кількість речовин одного класу небезпеки; Сі – середньомісячна концентрація і-го забруднювача; ГДКі - гранично допустима концентрація і-го забруднювача; bі – ваговий коефіцієнт даної речовини в залежності від класу небезпеки; y - пріоритетний індекс середовища (для повітря = 3).
6. Оцінка рівнів шуму в балах здійснюється за формулою:
де Lекв – фактичний середньоеквівалентний рівнь шуму, дБА; ГДР – гранично допустимий рівень шуму, дБА; b – ваговий коефіцієнт; y – пріоритетний індекс (для шуму = 2).
7. Методика оцінки рівнів забруднення ґрунту екзогенними хімічними речовинами базується на розрахунку середньорічного індексу територіального навантаження. Спочатку розраховують індекс для кожної речовини окремо:
де Мi – кількість технічного препарату, використаного для обробки ґрунту в зоні спостереження за кілька років, кг/га; Z i - % вмісту діючої речовини в технічному препараті; n – кількість років внесення; K i – середній оцінний бал препарату, що враховує такі його властивості, як токсичність, стійкість, летючість і кумуляція. Далі всі індекси, розраховані по кожній речовині, підсумовують і ділять на їхню кількість (m):
8. Стан навколишнього середовища в зоні спостереження, виражений у балах, оцінюють як суму балів окремих середовищ біосфери та оремих факторів: Р = Ратм + Ргрунт + Рвода + Ршум + Рхарч.прод.
9. Оцінку житлово-побутових умов населення в балах проводять, використовуючи формулу:
де К1,2,3 – груповий ваговий коефіцієнт (К1 = 1,0; К2 = 1,0; К3 = 2,0); Ф1,2,3 – фактичне число балів по групі показників; М1,2,3 – максимальне число балів для даного показника (М1 = 10,0; М2 = 12,0; М3 = 10,0); у – пріоритетний індекс фактору. Методика вивчення впливу довкілля на здоров¢я населення
Інформацію про показники, які характеризують стан здоров¢я населення (наприклад – про рівень захворюваності, смертності, інвалідності або фізичного розвитку) отримують з різних джерел інформації, перерахованих на першому занятті цього розділу. Для моделювання взаємозв’язків у системі «навколишнє середовище - здоров¢я населення» та встановлення кількісної величини такого зв’язку використовують математико-статистичний метод, результатом якого є розрахунок узагальнених індексів здоров¢я, що характеризують рівень здоров¢я населення, інтегруючи в собі ряд показників. Вимоги до індексів: 1) доступність даних для розрахунку індексу; 2) повнота охоплення населення; 3) якість (дані не повинні змінюватися в часі та просторі); 4) розрахунковість – простота і невисока вартість розрахунку; 5) прийнятність методу розрахунку та оцінки; 6) відтворюваність різними спеціалістами; 7) специфічність (відбиває зміни тільки в тих явищах, відтворюванням яких є); 8) чутливість до змін відповідних явищ; 9) валідність (міра істинного вираження); 10) репрезентативність; 11) ієрархічність; 12) відповідність меті.
Методика розрахунку інтегрального індексу здоров¢я (за Л.Є.Поляковим та Д.М.Малиським) 1 етап: відбір найбільш інформативних показників, що характеризують здоров¢я населення в зоні спостереження. 2 етап: розрахунок окремих показників здоров¢я для кожної зони спостереження(Мі). 3 етап: розрахунок середніх величин для кожної зони спостереження (М) та середнього квадратичного відхилення і-показника у зоні спостереження (σі). 4 етап: Розрахунок нормованих до середнього рівня показників здоров¢я окремо для кожної зони спостереження за формулою (wі):
wі = (Мі – М) / σ,
де wі – нормований показник здоров’я; Мі – значення окремого показника здоров’я; М – середнє значення показника здоров’я; σ - середнє квадратичне відхилення показника у зоні спостереження. 5 етап: заміна нормованих показників (wі) ймовірними одиницями (bі) за спеціальною таблицею 1: Таблиця 1 Заміна нормованих показників здоров¢я (wі) ймовірними одиницями (bі)
6 етап: розрахунок середньої ймовірності одиниці (у) показників здоров¢я для кожної зони спостереження за формулою:
у = Sbі / n, де Sbі – сума ймовірності одиниць по зоні спостереження; n – кількість відібраних показників здоров¢я. 7 етап: розрахунок інтегрального індексу здоров¢я (К): К=(1–у) х 100% (табл. 2). Таблиця 2 Розрахунок інтегрального індексу здоров¢я
Таким чином, ми отримуємо цифровий індекс, який можна порівнювати. Також слід зазначити, що цей метод розрахунку простий, доступний та інформативний. Якщо всі етапи розрахунку були проведені без помилок, то при повному благополуччі навколишнього середовища узагальнений індекс дорівнює приблизно 65-70%. Таблиця 3
Розподіл населення на групи здоров¢я за його критеріями
Таблиця 4
Орієнтовна шкала структури первинної захворюваності міського населення за зверненнями, %
Таблиця 5
Процент осіб І-ІІ груп здоров¢я в окремих віково-статевих групах населення
4. Методи математичної статистики в аналізі гігієнічних досліджень. Ступінь впливу денатурованої біосфери на здоров’я людей. Поняття про адаптацію та компенсацію організму до впливу чинників навколишнього середовища. Стадії адаптації. Математична статистика — розділ математики, в якому на основі дослідних даних вивчаються імовірнісні закономірності масових явищ. Основними задачами математичної статистики є статистична перевірка гіпотез, оцінка розподілу статистичних імовірностей та його параметрів, вивчення статистичної залежності, визначення основних числових характеристик випадкових вибірок, якими є: вибіркове середнє, вибіркові дисперсії, стандартне відхилення. Прикладом перевірки таких гіпотез є з'ясування питання про те, змінюється чи не змінюється виробничий процес з часом. Прикладом оцінки параметрів є оцінка середнього значення статистичної змінної за дослідними даними. Для вивчення статистичної залежності використовують методи теорії кореляції. Загальні методи математичної статистики є основою теорії похибок. Математичною статистикою називається наука, що займається розробкою методів отримання, опису і обробки експериментальних даних з метою вивчення закономірностей випадкових масових явищ. Всі задачі математичної статистики умовно можна розділити на дві групи. Першою з них є розробка методів збору і групування статистичних даних, отриманих в результаті спостережень, опрацювання статистичних звітів чи даних в результаті спеціально поставлених експериментів. Друга задача полягає в розробці методів аналізу статистичних даних залежно від мети. Сюди належать: а) оцінка ймовірності події; знаходження функції розподілу випадкової величини; оцінка залежності випадкової величини від інших випадкових величин, тощо; оцінка невідомих параметрів розподілу; б) перевірка статистичних гіпотез про зроблені вище припущення. Висновки за допомогою методів математичної статистики, зроблені зі зібраних статистичних даних, повинні правильно відображати загальні ймовірнісні характеристики процесу, що досліджується. Сучасна математична статистика розробляє способи визначення числа необхідних випробувань до початку дослідження (планування експерименту), а в ході досліджень вказує, як проводити послідовний аналіз даних. Тому, в деяких підручниках, її визначають як науку про прийняття рішень в умовах невизначеності. [8] Математична статистика широко використовує методи теорії ймовірностей. Методи математичної статистики широко застосовують в організації виробництва, радіотехніці, військовій справі, теорії автоматичного керування, біології, економіці, статистичній фізиці, зоряній астрономії тощо. Математичну статистику використовують також при розв'язанні теоретичних і практичних задач кібернетики. Порівняно новим напрямом розвитку математичної статистики є послідовний аналіз та загальна теорія статистичних рішень, яка тісно пов'язана з теорією ігор. [7] В будь-якому дослідженні об'єктивність результатів залежить від точності виміру явищ, їх аналізу і обробки. Статистичні методи дозволяють систематизувати, науково опрацювати і подати матеріали дослідження, перевірити їх наукову достовірність. [1]
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.74.47 (0.008 с.) |



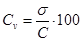 .
.