
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение напряжений по методу угловых точекСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Метод угловых точек применяется для определения величины сжимающих напряжений в любой точке нагруженной площади, когда она может быть разбита на прямоугольники таким образом, чтобы рассматриваемая точка оказалась угловой. Сжимающие напряжения в этой точке для горизонтальных площадок, параллельных плоской границе полупространства, определяются согласно формуле (42') и будут равны алгебраической сумме напряжений от прямоугольных площадей загрузки, для которых эта точка является угловой. Комбинация следующих случаев дает возможность находить вертикальные сжимающие напряжения в любой точке загруженного грунтового массива.
Рис. 14. Схема к расчету напряжений по методу угловых точек
1. Точка М проецируется на контур загруженного прямоугольника (рис. 14, а). Напряжение в точке М определяется как сумма двух угловых напряжений в прямоугольниках Mabe (I) и Meсd (II).
2. Точка М лежит на вертикали, проходящей внутри загруженного прямоугольника (рис. 14, б). Напряжение в т. М определяется как сумма четырех угловых напряжений в прямоугольниках Mhbe (I), Mecf (II), Mfdg (III) и Mgah (IV).
3. Точка M лежит на вертикали, проходящей вне границы контура загружения (рис. 14, в). Напряжение в точке М равно сумме угловых напряжений в прямоугольниках Mhbe (I) и Mecf (II), взятых со знаком плюс, и в прямоугольниках Mgdf (III) и Mhag (IV), взятых со знаком минус.
В вышеприведенных формулах Таблица 7 Коэффициент а
Примечания: 1. В таблице обозначено: b - ширина или диаметр фундамента; l - длина фундамента. 2. Для фундаментов, имеющих подошву в форме правильного многоугольника с площадью А, значения α принимаются, как для круглых фундаментов радиусом 3. Для промежуточных значений ζ и η коэффициент α определяется по интерполяции.
Пример: Определить величину сжимающих напряжений под центром и под серединой длинной стороны загруженного прямоугольника размерами 4x9,6 м на глубине 4 м от поверхности при внешней нагрузке интенсивностью Р=300 кПа. Для площадки под центром загруженной площади:
По табл. 7: а =0,505.
Для площадки под серединой длинной стороны прямоугольной загруженной площади, разделяя ее на два прямоугольника размерами 4x4,8 м так, чтобы рассматриваемая точка была угловой:
Определение напряжений от нагрузки, Меняющейся по закону прямой
Сжимающие напряжения в массиве грунта при нагрузке, меняющейся по закону прямой, вычисляют по формуле
Рис. 15. Номограмма для определения сжимающих напряжений от нагрузки, меняющейся по закону прямой
Величина
Рис. 16. Схемы нагрузок к примеру пользования номограммой (см. рис. 15)
Пример: Определить напряжение
По графику (рис. 15) При нагрузке, действующей справа:
Тогда Подставляя численные значения, получим
Для определения сжимающего напряжения
При фиктивной нагрузке:
Подставляя численные значения и учитывая фиктивность нагрузки klmn, получим
Для случая прямоугольной нагрузки (рис. 16, б)
Определив по графику (рис. 15)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 3654; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.102.163 (0.007 с.) |



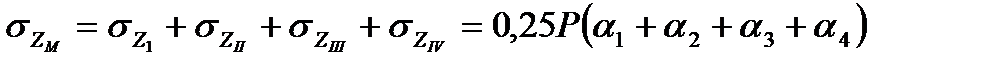

 - коэффициенты, принимаемые по табл. 7 в зависимости от соотношения сторон
- коэффициенты, принимаемые по табл. 7 в зависимости от соотношения сторон  площадей загружения I, II, III, IV и относительной глубины расположения точки М
площадей загружения I, II, III, IV и относительной глубины расположения точки М 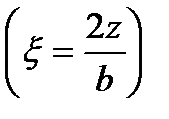 ; Р - интенсивность внешней равномерно распределенной нагрузки.
; Р - интенсивность внешней равномерно распределенной нагрузки.
 для фундаментов
для фундаментов


 .
.


 кПа
кПа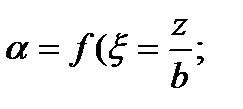



 =0,732.
=0,732. КПа.
КПа. (43)
(43) где
где  . Функция относительных величин
. Функция относительных величин 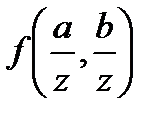 определяется по номограмме Остерберга (рис. 15); а и b — соответственно длины прямоугольной и треугольной эпюр нагрузки; z — глубина рассматриваемой точки.
определяется по номограмме Остерберга (рис. 15); а и b — соответственно длины прямоугольной и треугольной эпюр нагрузки; z — глубина рассматриваемой точки. определяется как алгебраическая сумма коэффициентов, соответствующих нагрузке слева и справа от вертикали, проходящей через рассматриваемую точку.
определяется как алгебраическая сумма коэффициентов, соответствующих нагрузке слева и справа от вертикали, проходящей через рассматриваемую точку.
 для точки M1 (рис. 16, а). При нагрузке, действующей слева:
для точки M1 (рис. 16, а). При нагрузке, действующей слева: и
и 
 =0,397.
=0,397. и
и 
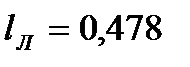


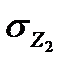 в точке М2 (рис. 16, а) прикладываем фиктивную нагрузку klmn. При полной нагрузке (включая фиктивную)
в точке М2 (рис. 16, а) прикладываем фиктивную нагрузку klmn. При полной нагрузке (включая фиктивную) и
и 



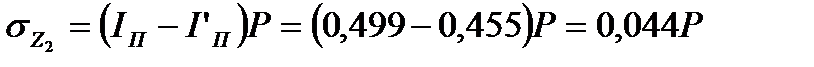

 при
при  и
и  (
( =0,278) и
=0,278) и  при
при  и
и  (
( =0,410), получим
=0,410), получим



