
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение напряжений от действия сосредоточенной силыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рис. 11. Схема к определению напряжений от действия сосредоточенной силы В строительной практике наибольший интерес представляет закономерность распределения нормальных вертикальных напряжений σZ. В грунтовом массиве возьмем т. М, положение которой определяется полярными координатами R и β, в системе координат с началом в точке О приложения силы N. Для упрощения вывода примем как постулат, что напряжение σR пропорционально Сosβ и обратно пропорционально квадрату расстояния R2 от точки приложения сосредоточенной силы до т. М:
где А - коэффициент пропорциональности, определяемый из условия равновесия:
Подставив значение А из формулы (35) в формулу (34), получим
Отнесем величину радиальных напряжений не к площадке, перпендикулярной к радиусу, а к площадке, параллельной ограничивающей плоскости и составляющей с ней угол
Положение точки М определяется двумя координатами z и r, тогда
где z - глубина рассматриваемой точки от ограничивающей полупространство плоскости; r - расстояние по горизонтали от т. М до оси Z, проходящей через точку О приложения сосредоточенной силы (рис. 11). Подставив значение R из формулы (38) в формулу (37), получим
Введя обозначение
Окончательно получим
где коэффициент К табулирован в зависимости от соотношения r/z (табл. 6).
Определение напряжений от действия нескольких Сосредоточенных сил
Рис. 12. Схема к расчету действия нескольких сосредоточенных сил
Если к поверхности линейно деформируемого полупространства приложить несколько сосредоточенных сил N1, N2, N3...Nn (рис. 12), то вертикальное сжимающее напряжение
Значения коэффициентов К определяют из табл. 6 в зависимости от соотношения r/z.
Определение напряжений от действия равномерно распределенной нагрузки по прямоугольной площади
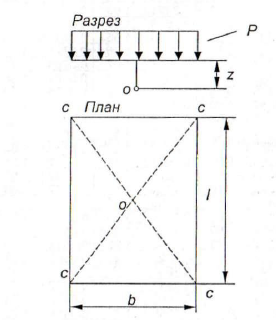
Практический интерес для строителей представляет задача об упругом полупространстве, загруженном вертикальной равномерно распределенной нагрузкой интенсивностью Р на прямоугольной площади размером Ixb (рис.13). Эта задача используется в механике грунтов для определения напряжений в основаниях прямоугольных фундаментов.
Таблица 6 Значение коэффициента К для вычисления сжимающих напряжений от действия сосредоточенной силы в зависимости от отношения r/z
Рис. 13. Схема к расчету действия равномерно распределенной площадной нагрузки
Вертикальная составляющая напряжений σZ0 в точках, расположенных на различной глубине под центром прямоугольной площади, определяется по формуле:
где l - длина; b - ширина прямоугольной площадки загружения; z - глубина рассматриваемой точки. Введем обозначение
Тогда формула (41) примет вид
Для точек, расположенных под углами загруженной площади, вертикальная составляющая напряжений определится по формуле
где α - коэффициент рассеивания напряжений с глубиной, принимается в зависимости от формы подошвы фундамента, соотношения сторон прямоугольного фундамента
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1590; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.235.107 (0.007 с.) |

 От действия силы N, приложенной в т. О перпендикулярно к горизонтальной плоскости, ограничивающей линейно деформируемое полупространство (рис.11), во всех точках полупространства, удаленных от т. О, возникает сложное напряженное состояние, характеризующееся напряжениями
От действия силы N, приложенной в т. О перпендикулярно к горизонтальной плоскости, ограничивающей линейно деформируемое полупространство (рис.11), во всех точках полупространства, удаленных от т. О, возникает сложное напряженное состояние, характеризующееся напряжениями  и перемещениями Sx, Sy, Sz.
и перемещениями Sx, Sy, Sz.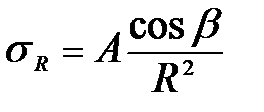 (34)
(34) (35)
(35)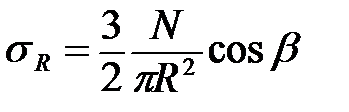 (36)
(36) . Получим
. Получим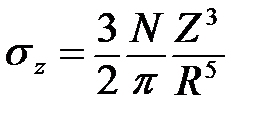 (37)
(37)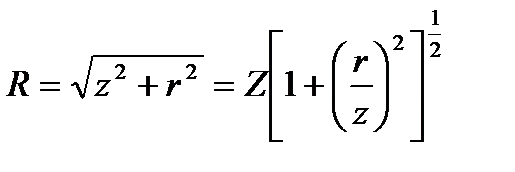 (38)
(38)
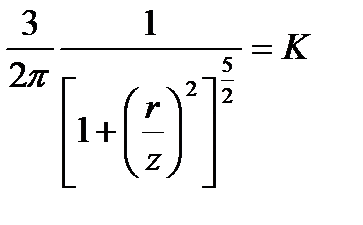
 (39)
(39)
 в любой точке грунтового массива определится простым суммированием, используя принцип суперпозиции, так как вывод формулы (39) предполагает прямую пропорциональность между напряжениями и деформациями.
в любой точке грунтового массива определится простым суммированием, используя принцип суперпозиции, так как вывод формулы (39) предполагает прямую пропорциональность между напряжениями и деформациями. (40)
(40)
 , (41)
, (41)
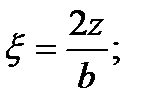
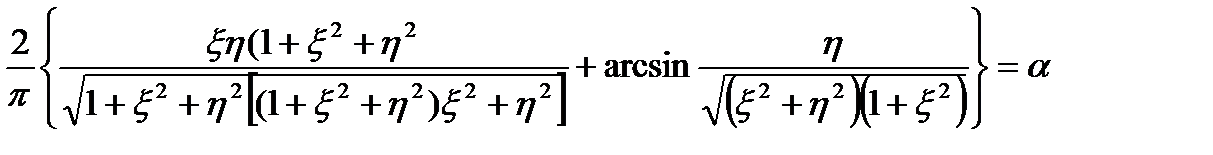
 (42)
(42)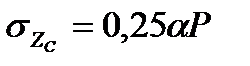 (42')
(42') и относительной глубины, равной
и относительной глубины, равной  при определении
при определении 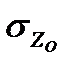 и
и  - при определении
- при определении 


