
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка устойчивости откосов и склонов методом круглоцилиндрических поверхностей скольженияСодержание книги
Поиск на нашем сайте
Метод круглоцилиндрических поверхностей скольжения широко применяется на практике. Сущность метода круглоцилиндрических поверхностей скольжения сводится к следующему. Предположим, что грунтовый массив смещается по круглоцилиндрической поверхности АС с центром в точке О (рис. 19). Условием равновесия призмы обрушения будет: сумма моментов всех сил относительно точки вращения 0 равна нулю, т.е. Силой, действующей на каждый отсек, будет его вес Принимаем условно за точку приложения веса каждого отсека точку пересечения отвесной линии (вес отсека) с серединой отрезка соответствующей дуги скольжения. Разложим вес отсека Qi на нормальную Ni (по направлению радиуса вращения) (Ni и касательную Ti (по направлению, перпендикулярному радиусу) составляющие к дуге скольжения в точке их приложения. Тогда
Момент сил, сдвигающих отсек относительно точек вращения О, определится по формуле
где
Рис. 19. Схема к расчету устойчивости откосов методом круглоцилиндрических поверхностей скольжения
Удерживающие силы
где li - длина дуги основания i -того отсека; φi - угол внутреннего трения; ci - сцепление грунта. Момент сил, удерживающих призму скольжения, определится по формуле
Коэффициент устойчивости η откоса будет равен отношению момента сил, удерживающих призму скольжения, к моменту сил сдвигающих:
Однако уравнение (61) не дает однозначного ответа на поставленный вопрос, так как можно провести множество круглоцилиндрических поверхностей с центром в точке О. Необходимо из всех возможных дуг поверхностей скольжения выбрать наиболее опасную. Для решения этой задачи с достаточным приближением применяют следующий прием.
Из верхней грани откоса проводят наклонную линию (вверх) под углом 36° к горизонту (рис. 20). На этой линии намечают точки
Рис. 20. Определение центра вращения наиболее опасной поверхности скольжения
Удерживающие силы
Для каждой дуги поверхности скольжения, проведенной из центров Как указывает Н.А. Цытович, некоторые усовершенствования и упрощения расчетов 'по методу круглоцилиндрических поверхностей скольжения внесены Г.И. Тер-Степаняном и М.Н. Гольдштейном. Коэффициент устойчивости в этом случае вычисляют по формуле
где А и В - коэффициенты, зависящие от геометрических размеров сползающей призмы, выраженные в долях от высоты откоса h. f=tgφ - коэффициент внутреннего трения. Значения этих коэффициентов и приведены в табл. 8. Величина h, вычисляемая из выражения (62), будет иметь вид
По формулам (62) и (63) и данным табл. 8 можно легко вычислить значения коэффициентов устойчивости откоса
Таблица 8 Значение коэффициентов А и В для приближенного расчета Устойчивости откосов
Пример. Определить предельную высоту откоса с уклоном 1:2, если
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 2067; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.76.21 (0.007 с.) |

 . Для составления уравнения моментов относительно точки вращения 0 разобьем призму скольжения АВС вертикальными сечениями на ряд отсеков. Разбивка призмы обрушения на отсеки производится с учетом неоднородности грунта призмы и профиля склона так, чтобы в пределах отрезка дуги скольжения основания каждого
. Для составления уравнения моментов относительно точки вращения 0 разобьем призму скольжения АВС вертикальными сечениями на ряд отсеков. Разбивка призмы обрушения на отсеки производится с учетом неоднородности грунта призмы и профиля склона так, чтобы в пределах отрезка дуги скольжения основания каждого  -го отсека прочностные характеристики
-го отсека прочностные характеристики  и
и  были бы постоянными.
были бы постоянными. .
.
 (57)
(57) (58)
(58) - число отсеков в призме обрушения.
- число отсеков в призме обрушения.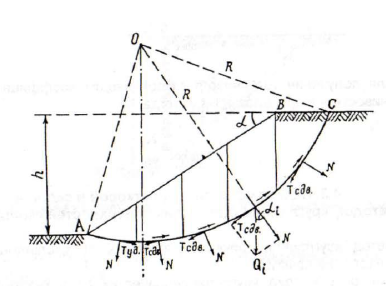
 в пределах основания каждого отсека будут обусловлены сопротивлением сдвигу за счет сил внутреннего трения, пропорциональных нормальной составляющей
в пределах основания каждого отсека будут обусловлены сопротивлением сдвигу за счет сил внутреннего трения, пропорциональных нормальной составляющей  , и сцепления грунта по поверхности скольжения:
, и сцепления грунта по поверхности скольжения: (59)
(59) (60)
(60) (61)
(61) и т.д. - центры дуг поверхностей скольжения - по следующему принципу. Точка
и т.д. - центры дуг поверхностей скольжения - по следующему принципу. Точка  находится на расстоянии (0,25 + 0,4m)h, где
находится на расстоянии (0,25 + 0,4m)h, где  ; h — высота откоса. Остальные центры последовательно отмечают на расстоянии 0,3h от предыдущего.
; h — высота откоса. Остальные центры последовательно отмечают на расстоянии 0,3h от предыдущего.
 (59)
(59) и т.д., определяют коэффициенты устойчивости по формуле (61). Минимальное значение коэффициента устойчивости определит положение наиболее опасной поверхности скольжения.
и т.д., определяют коэффициенты устойчивости по формуле (61). Минимальное значение коэффициента устойчивости определит положение наиболее опасной поверхности скольжения. (62)
(62) (63)
(63) и предельную высоту откоса h при принятой устойчивости.
и предельную высоту откоса h при принятой устойчивости.




 ,
,  22°,
22°,  =12 кПа,
=12 кПа,  =18 кН/м3. Поверхность скольжения проходит через нижнюю кромку откоса. Значения коэффициентов А и В находим по табл. 8. Подставив их в формулу (63), будем иметь
=18 кН/м3. Поверхность скольжения проходит через нижнюю кромку откоса. Значения коэффициентов А и В находим по табл. 8. Подставив их в формулу (63), будем иметь (м)
(м)


