
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сопротивление грунтов сдвигуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Значение касательного напряжения т, при котором происходит сдвиг (смещение одной части грунта по отношению к его другой части под действием постоянно возрастающего сдвигающего усилия), называется предельным сопротивлением грунтов сдвигу. Одним из способов определения сопротивления грунтов сдвигу является испытание их на прямой срез в одноплоскостных сдвиговых приборах в соответствии с требованиями ГОСТ 12248-78 "Грунты. Методы лабораторного определения сопротивления срезу". К помещенному в прибор образцу грунта ступенчато прикладывают вертикальное давление, под действием которого происходит уплотнение грунта. После достижения данной величины давления и стабилизации деформации грунта к верхней (или нижней) обойме прибора - в зависимости от его конструкции - прикладывают горизонтальное давление до тех пор, пока не произойдет горизонтальное перемещение одной части образца грунта по другой. Величина перемещения фиксируется индикатором. Испытание следует считать законченным, когда произойдет мгновенный срез одной части образца по отношению к другой или общая деформация среза составит 5 мм. Такие испытания проводят для нескольких образцов грунта (минимум трех), находящихся в одинаковом состоянии при различных значениях вертикальных давлений Р. С увеличением сжимающих напряжений, действующих на образец, предельные касательные напряжения По результатам испытаний для нескольких образцов при различных нормальных напряжениях Для этого через опытные точки проводят прямую линию, занимающую среднее положение между всеми точками. Для этого через опытные точки проводят прямую линию, занимающую среднее положение между всеми точками. Опытами установлено, что график зависимости предельного сопротивления грунтов сдвигу от нормального напряжения для идеально сыпучих грунтов в пределах изменений напряжений, представляющих интерес для строительства (0,1-0,6 МПа), с достаточной степенью точности может быть принят за прямую линию, выходящую из начала координат и наклоненную под углом φ к оси нормальных напряжений (рис. 9).
Рис. 9. График зависимости сопротивления сдвигу от нормального напряжения для песков
Согласно графику, зависимость между касательным и нормальным напряжениями выражается уравнением
или где f=tgφ - коэффициент внутреннего трения. Угол φ - угол внутреннего трения - является прочностной характеристикой для песков. Он может быть получен по графику зависимости
Выражение (31) является основной прочностной зависимостью для сыпучих грунтов, носит название закона Кулона и формулируется следующим образом: предельное сопротивление сыпучих грунтов сдвигу есть сопротивление трению, прямо пропорциональное нормальному напряжению. Для глинистых грунтов зависимость между касательными и нормальными напряжениями
Рис. 10. График зависимости сопротивления сдвигу от нормального напряжения для глинистых грунтов
Эта зависимость описывается уравнением
где φ - угол внутреннего трения, с - сцепление грунта. Приняв f=tg(φ), уравнение (32) примет вид
Коэффициент f=tg Угол внутреннего трения φ и удельное сцепление с являются прочностными характеристиками глинистых грунтов. Уравнение (32) выражает закон Кулона для глинистых грунтов, который формулируется следующим образом: «предельное сопротивление связных грунтов сдвигу при завершенной их консолидации есть функция первой степени от нормального напряжения».
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 732; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.239.111 (0.007 с.) |

 возрастают.
возрастают. строят график зависимости касательных и нормальных напряжений
строят график зависимости касательных и нормальных напряжений  .
.
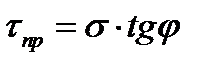 , (31)
, (31) , (31')
, (31')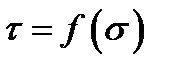 или вычислен из выражения
или вычислен из выражения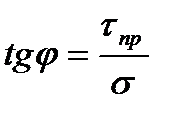
 имеет более сложный характер в связи с тем, что сопротивление сдвигу глинистых грунтов обусловлено не только силами трения, но и связностью грунта. Однако, как и для сыпучих грунтов, зависимость предельного сопротивления сдвигу от нормальных напряжений представляется прямой линией (рис. 10).
имеет более сложный характер в связи с тем, что сопротивление сдвигу глинистых грунтов обусловлено не только силами трения, но и связностью грунта. Однако, как и для сыпучих грунтов, зависимость предельного сопротивления сдвигу от нормальных напряжений представляется прямой линией (рис. 10).
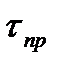 =
=  , (32)
, (32) (32')
(32') по аналогии с сыпучими грунтами носит название коэффициента внутреннего трения. Параметр с называется удельным сцеплением глинистых грунтов и характеризует их связность.
по аналогии с сыпучими грунтами носит название коэффициента внутреннего трения. Параметр с называется удельным сцеплением глинистых грунтов и характеризует их связность.


