
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Угловые характеристики синхронного генератораСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Электромагнитная мощность неявнополюсного синхронного генератора при его параллельной работе с сетью где Электромагнитная мощность явнополюсного синхронного генератора
где Разделив выражения (21.7) и (21.8) на синхронную угловую скорость вращения неявнополюсной синхронной машины
явнополюсной синхронной машины
где М — электромагнитный момент, Нм. Анализ выражения (21.10) показывает, что электромагнитный момент явнополюсной машины имеет две составляющие: одна из них представляет собой основную составляющую электромагнитного момента
другая — реактивную составляющую момента
Основная составляющая электромагнитного момента
Это свидетельствует о том, что основная составляющая электромагнитного момента Реактивная составляющая электромагнитного момента При увеличении нагрузки синхронного генератора, т. е. с ростом тока I1 происходит увеличение угла Рассмотрим угловые характеристики электромагнитной мощности
Рис. 21.5. Угловая характеристика синхронного генератора.
Максимальное значение электромагнитного момента Как видно из результирующей угловой характеристики (график 3), при увеличении нагрузки синхронной машины до значений, соответствующих углу При нагрузке, соответствующей углу Электромагнитный момент, соответствующий критическому значению угла ( Для явнополюсных синхронных машин
У неявнополюсных синхронных машин Отношение максимального электромагнитного момента Мmax к номинальному
Пренебрегая реактивной составляющей момента, можно записать
т.е. чем меньше угол Пример 21.1. Трехфазный синхронный генератор с явно выраженными полюсами на роторе ( Требуется рассчитать значения электромагнитных моментов и построить графики Решение. Полное индуктивное сопротивление реакции якоря по (20.19)
При
Индуктивное сопротивление реакции якоря по продольной оси [см. (20.24)]
по поперечной оси [см. (20.25)]
Синхронные индуктивные сопротивления по продольной и поперечной осям:
ЭДС обмотки статора в режиме х.х. по (21.13)
Напряжение фазы обмотки статора
Угловая частота вращения ротора
Максимальное значение основной составляющей электромагнитного момента генератора (21.11)
Максимальное значение реактивной составляющей электромагнитного момента (21.12)
Результаты расчета моментов
Угол
где
Углу
Графики моментов
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 778; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.116 (0.009 с.) |

 (21.7)
(21.7) - угол, на который продольная ось ротора смещена относительно продольной оси результирующего поля машины (рис. 21.4).
- угол, на который продольная ось ротора смещена относительно продольной оси результирующего поля машины (рис. 21.4). (21.8)
(21.8) и
и  — синхронные индуктивные сопротивления явнополюсной синхронной машины по продольно и поперечной осям соответственно, Ом.
— синхронные индуктивные сопротивления явнополюсной синхронной машины по продольно и поперечной осям соответственно, Ом. , получим выражения электромагнитных моментов:
, получим выражения электромагнитных моментов: (21.9)
(21.9) (21.10)
(21.10) . (21.11)
. (21.11) . (21.12)
. (21.12) явнополюсной синхронной машины зависит не только от напряжения сети (
явнополюсной синхронной машины зависит не только от напряжения сети ( U1), но и от ЭДС
U1), но и от ЭДС  , наведенной магнитным потоком вращающегося ротора
, наведенной магнитным потоком вращающегося ротора  в обмотке статора:
в обмотке статора: .(21.13)
.(21.13) не зависит от магнитного потока полюсов ротора. Для возникновения этой составляющей достаточно двух условий: во-первых, чтобы ротор машины имел явновыраженные полюсы (
не зависит от магнитного потока полюсов ротора. Для возникновения этой составляющей достаточно двух условий: во-первых, чтобы ротор машины имел явновыраженные полюсы ( ) и, во-вторых, чтобы к обмотке статора было подведено напряжение сети (
) и, во-вторых, чтобы к обмотке статора было подведено напряжение сети ( ). Подробнее физическая сущность реактивного момента будет изложена в § 23.2.
). Подробнее физическая сущность реактивного момента будет изложена в § 23.2.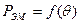 и
и  , представленные графически, называются угловыми характеристиками синхронной машины.
, представленные графически, называются угловыми характеристиками синхронной машины. и электромагнитного момента
и электромагнитного момента  ) и магнитного потока возбуждения, т. е.
) и магнитного потока возбуждения, т. е.  и электромагнитной мощности
и электромагнитной мощности  от угла
от угла 
 соответствует критическому значению угла
соответствует критическому значению угла  .
.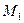 сумме противодействующих моментов, т. е.
сумме противодействующих моментов, т. е.  . В результате частота вращения ротора остается неизменной, равной синхронной частоте вращения.
. В результате частота вращения ротора остается неизменной, равной синхронной частоте вращения. вызывает увеличение частоты вращения ротора, что ведет к нарушению условий синхронизации (машина выходит из синхронизма).
вызывает увеличение частоты вращения ротора, что ведет к нарушению условий синхронизации (машина выходит из синхронизма). (21.14)
(21.14) . (21.15)
. (21.15) = 0, а поэтому угловая характеристика представляет собой синусоиду и угол
= 0, а поэтому угловая характеристика представляет собой синусоиду и угол  называется перегрузочной способностью синхронной машины или коэффициентом статической перегружаемости:
называется перегрузочной способностью синхронной машины или коэффициентом статической перегружаемости: . (21.16)
. (21.16) , (21.17)
, (21.17) , соответствующий номинальной нагрузке синхронной машины, тем больше ее перегрузочная способность. Например, у турбогенератора
, соответствующий номинальной нагрузке синхронной машины, тем больше ее перегрузочная способность. Например, у турбогенератора  = 2,35÷2,0.
= 2,35÷2,0. =10) включен на параллельную работу с сетью напряжением 6000 В частотой 50 Гц. Обмотка статора соединена звездой и содержит в каждой фазе
=10) включен на параллельную работу с сетью напряжением 6000 В частотой 50 Гц. Обмотка статора соединена звездой и содержит в каждой фазе  = 310 последовательных витков, обмоточный коэффициент
= 310 последовательных витков, обмоточный коэффициент  = 0,92, индуктивное сопротивление рассеяния обмотки
= 0,92, индуктивное сопротивление рассеяния обмотки  = 10 Ом. Диаметр расточки D1 = 0,8 м, расчетная длина сердечника статора li = 0,28 м, воздушный зазор равномерный δ = 2 мм, коэффициент полюсного перекрытия
= 10 Ом. Диаметр расточки D1 = 0,8 м, расчетная длина сердечника статора li = 0,28 м, воздушный зазор равномерный δ = 2 мм, коэффициент полюсного перекрытия  =0,7, коэффициент воздушного зазора kδ = 1,3, коэффициент магнитного насыщения
=0,7, коэффициент воздушного зазора kδ = 1,3, коэффициент магнитного насыщения  = 1,1. Магнитный поток ротора Ф = 0,058 Вб.
= 1,1. Магнитный поток ротора Ф = 0,058 Вб. Ом
Ом = 0,7 и равномерном зазоре коэффициенты формы поля по (20.7) и (20.8):
= 0,7 и равномерном зазоре коэффициенты формы поля по (20.7) и (20.8): = 0,958 и
= 0,958 и  = 0,442.
= 0,442. Ом,
Ом, Ом.
Ом. Ом,
Ом, Ом.
Ом. В.
В. В.
В.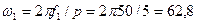 с-1.
с-1. Н∙м
Н∙м Н·м
Н·м для ряда значений угла 0 приведены ниже:
для ряда значений угла 0 приведены ниже:
 ,
, ;
; 0,48 = 61,3°.
0,48 = 61,3°. Н∙м;
Н∙м; Н∙м;
Н∙м; Н∙м.
Н∙м. , построенные по результатам расчета, приведены на рис 21.6.
, построенные по результатам расчета, приведены на рис 21.6.


