
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм вычисления обратной матрицы второго и третьего порядков (метод присоединённой матрицы)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Найдите определитель матрицы 2. Транспонируйте матрицу 3. Найдите алгебраические дополнения элементов матрицы 4. Вычисляем обратную матрицу 5. Проверить правильность вычисления обратной матрицы по формуле: Пример. Найти матрицу, обратную к матрице Решение: Применим алгоритм нахождения обратной матрицы. 1. Найти определитель матрицы
Матрица имеет обратную матрицу, так как 2. Найдем матрицу 3. Найдем алгебраические дополнения элементов матрицы
Составим союзную матрицу: 4. Вычисляем обратную матрицу
5. Проверим правильность вычисления обратной матрицы по формуле:
Ответ. Выберите свой вариант и решите задачу.
Задание 4. Решить систему: а) методом Крамера; б) методом обратной матрицы. а)Решить систему линейных уравнений по формулам Крамера. Рассмотрим систему трёх линейных уравнений с тремя неизвестными
Система имеет единственное решение при условии, что определитель системы отличен от нуля, т.е.
Формулы (*) называются формулами Крамера. Теорема Крамера. Система
Рассмотрим случай, когда определитель системы равен нулю. Здесь возможны два варианта 1. 2. Например, для системы из трёх уравнений:
Ответ. Алгоритм: 1. Вычислите определитель матрицы 2. Заменяя первый второй и третий (поочередно) столбцы матрицы 3. Подставить найденные определители в формулу (*): 4. Запишите ответ. Пример. Решить систему линейных уравнений по формулам Крамера
Решение. 1. Найдем определитель матрицы системы 2. Заменим первый столбец матрицы Заменим второй столбец матрицы
Для нахождения неизвестной 3. Находим неизвестную 4. Ответ. б) Решить систему линейных уравнений методом обратной матрицы (матричным методом) Рассмотрим систему уравнений
Данная система может быть записана в матричном виде
Тогда решение системы (3.1.) имеет вид Алгоритм: 1. Составить матрицу системы из коэффициентов при переменных 2. Найти матрицу 3. Умножить обратную матрицу на матрицу столбец свободных членов Пример. Решить систему методом обратной матрицы (матричным методом)
Решение.
Составить матрицу системы из коэффициентов при переменных Алгебраические дополнения
Матрица из алгебраических дополнений Обратная матрица Находим решение системы
Ответ. Выберите свой вариант и решите задачу.
Задание 5. Решить систему методом Гаусса. При решении систем линейных уравнений используют также метод Гаусса (метод последовательного исключения неизвестных). Он состоит в следующем: систему уравнений приводят к эквивалентной ей системе со ступенчатой матрицей (системы называются эквивалентными, если множества их решений совпадают). Эти действия называют прямым ходом. Из полученной ступенчатой системы переменные находят с помощью последовательных подстановок (обратный ход). При выполнении прямого хода используют следующие преобразования: 1) умножение и деление коэффициентов и свободных членов на одно и то же число; 2) сложение и вычитание уравнений; 3) перестановку уравнений в системе; 4) исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулю. Алгоритм: 1.Выпишите расширенную матрицу системы 2. Методом элементарных преобразований свести расширенную матрицу к ступенчатому виду 3. Запишите систему, эквивалентную матрице, полученной в пункте 2. 4. Выполняя «обратный ход» решите полученную систему. «Поднимитесь» от последнего уравнения к первому. 5. Запишите ответ. Примервыполнения задания. а) Решение. Запишем расширенную матрицу системы
Умножаем первую строку на 3 и складываем со второй
Результат запишем вместо второй строки. Умножаем первую строку на 2 и вычитаем из результата третью строку
Результат запишем вместо третьей строки. Умножаем первую строку на 2 и вычитаем из результата четвертую строку
Результат записываем вместо четвертой строки
Первый ненулевой элемент во второй строке указан и обведены
Запишем эквивалентную систему
В эквивалентной системе получили противоречивое равенство (последняя строка 0=1). Поэтому система несовместна. Ответ. Система несовместна. б) Решить систему методом Гаусса Решение. 1.Запишем расширенную матрицу системы
Здесь уже указан первый ненулевой первой строки и обведены элементы под ним, которые нужно занулить. Для зануления требуемых элементов выполнить действия: Из первой строки вычесть две вторые строки. Результат записать вместо второй строки. Первую строку умножить на 3 и из результата вычесть две третьи строки. Результат записать вместо третьей строки. Из первой строки вычесть две четвертые строки. Результат записать вместо четвертой строки. Результат всех действий
Здесь указан первый ненулевой элемент второй строки и обведены элементы под ним, которые нужно занулить. Схематически указаны требуемые действия:
Вторую строку умножаем на 13 и из результата вычитаем девять третьих строк. Вторую строку складываем с тремя четвертыми строками. Результат действий
Нулевую строку вычеркиваем. Вторую строку можно разделить на 3. Результат действий
Первые ненулевые находятся в первом, третьем и пятом столбце. Поэтому
Независимые переменные переносим в правые части уравнений
4. Поднимаемся от последнего уравнения к первому 1) 2) 3)
Ответ: Выберите свой вариант и решите задачу.
Задание 6. Вычислить площадь параллелограмма, построенного на векторах Площадь параллелограмма, построенного на векторах равна длине вектора, равного векторному произведению заданных векторов. Алгоритм: 1. Найдите векторное произведение векторов по формуле коэффициенты при единичных векторах 2. Вычислите модуль найденного векторного произведения по формуле
3. Запишите ответ. Пример решения задания: Вычислить площадь параллелограмма, построенного на векторах
Коэффициенты при единичных векторах Найдем его длину
Выберите свой вариант и решите задачу.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 616; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.62.85 (0.011 с.) |

 . Если определитель отличен от нуля, то матрица имеет обратную матрицу.
. Если определитель отличен от нуля, то матрица имеет обратную матрицу. . Заменим каждый элемент матрицы
. Заменим каждый элемент матрицы  ,
,  – дополнительный минор, он равен определителю матрицы, которая получается вычёркиванием i -ой строки и j -го столбца. Составьте союзную (присоединённую)
– дополнительный минор, он равен определителю матрицы, которая получается вычёркиванием i -ой строки и j -го столбца. Составьте союзную (присоединённую)  матрицу из алгебраических дополнений транспонированной матрицы.
матрицу из алгебраических дополнений транспонированной матрицы.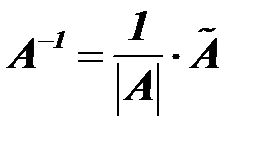 .
. .
. .
.
 .
. , транспонированную к матрице
, транспонированную к матрице  .
. . Заменим каждый элемент матрицы
. Заменим каждый элемент матрицы  ,
,  – дополнительный минор, он равен определителю матрицы, которая получается вычёркиванием i -ой строки и j -го столбца.
– дополнительный минор, он равен определителю матрицы, которая получается вычёркиванием i -ой строки и j -го столбца.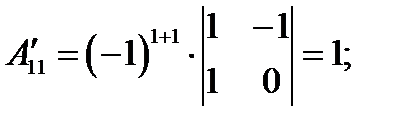







 .
.
 .
.

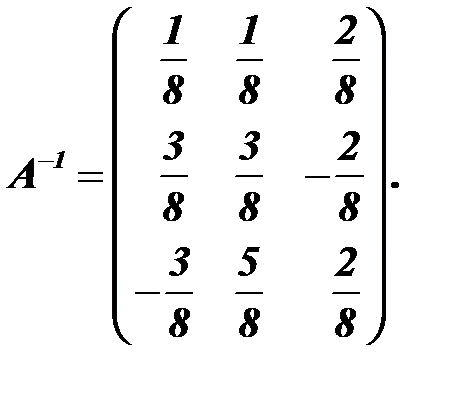










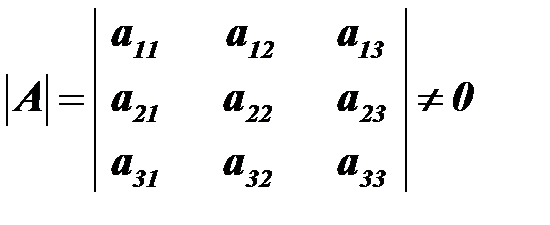 , которое определяется по формулам
, которое определяется по формулам  (*), где
(*), где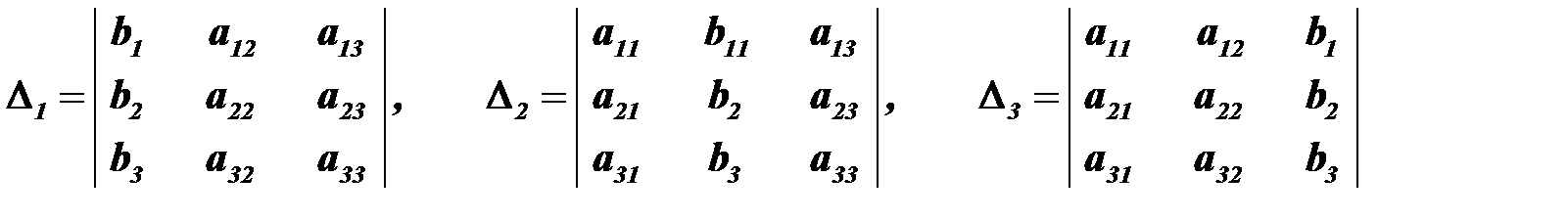
 уравнений с
уравнений с  и каждый определитель
и каждый определитель  . Это имеет место только тогда, когда коэффициенты при неизвестных
. Это имеет место только тогда, когда коэффициенты при неизвестных  пропорциональны, то есть каждое уравнение системы получается из первого уравнения умножением обеих его частей на число
пропорциональны, то есть каждое уравнение системы получается из первого уравнения умножением обеих его частей на число  . Очевидно, что при этом система имеет бесчисленное множество решений.
. Очевидно, что при этом система имеет бесчисленное множество решений. . Это имеет место только тогда, когда коэффициенты при всех неизвестных, кроме
. Это имеет место только тогда, когда коэффициенты при всех неизвестных, кроме 
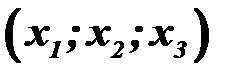 .
. .
.
 .
.
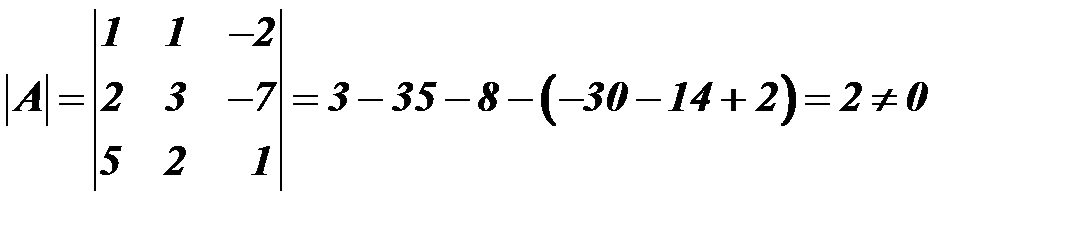 . Выпишем столбец свободных членов
. Выпишем столбец свободных членов 
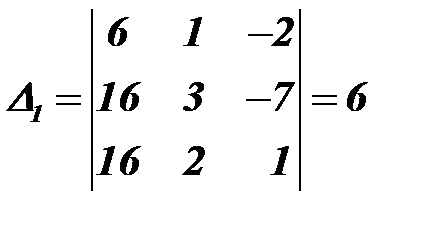 . Тогда
. Тогда  .
. . Находим неизвестную
. Находим неизвестную  .
. в матрице
в матрице 
 .
. .
. , где
, где
 (
( обратная матрица).
обратная матрица). , матрицу- столбец свободных членов
, матрицу- столбец свободных членов  .
.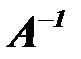 , обратную к матрице
, обратную к матрице 

 , матрицу- столбец свободных членов
, матрицу- столбец свободных членов  . Найдем матрицу обратную матрице системы:
. Найдем матрицу обратную матрице системы: 
 .
. ,
,  ,
, 
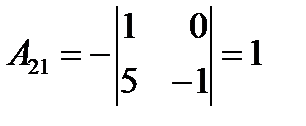 ,
,  ,
, 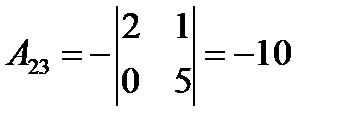 ,
, ,
,  ,
, 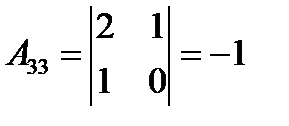 .
. .
.


 ,
,  ,
, 
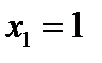 ,
,  ,
,  .
.



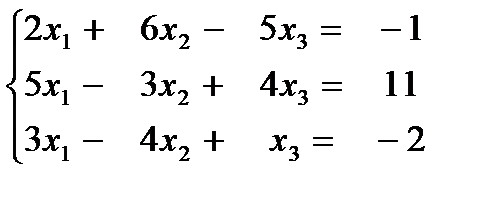
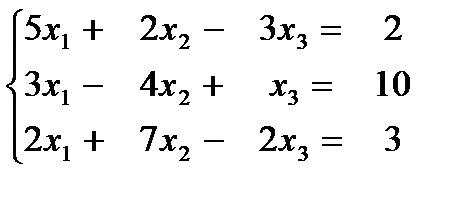





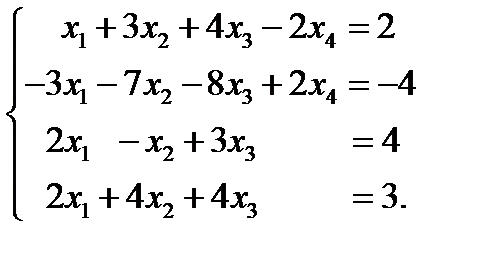
 .
.
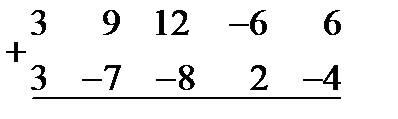
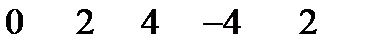




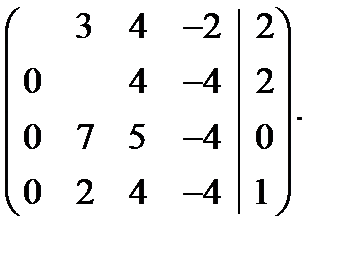



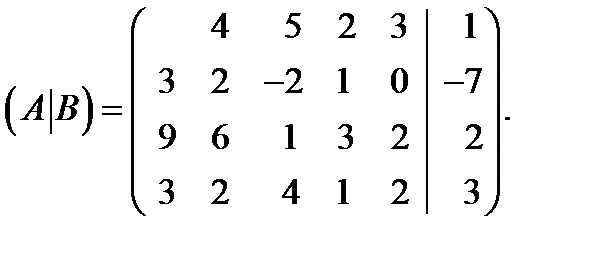


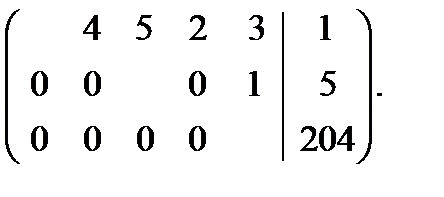
 ,
,  ,
,  –зависимые переменные, остальные
–зависимые переменные, остальные  ,
,  – независимые переменные. Запишем эквивалентную систему
– независимые переменные. Запишем эквивалентную систему


 .
.



 ,
,  ,
,  .
.


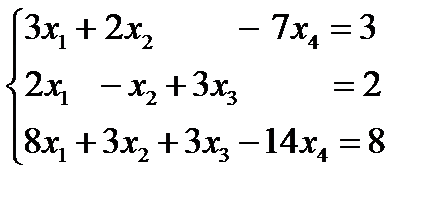






 и
и 
 ,
, полученного произведения есть координаты вектора
полученного произведения есть координаты вектора  .
. .
. и
и  .
.
 .
. . Длина вектора и есть искомая площадь.
. Длина вектора и есть искомая площадь. .
. (1; 2; 3)
(1; 2; 3)  (-1; 3; 2)
(-1; 3; 2)



