
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм вычисления пределов функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
а) представляющих, дробно-рациональную функцию; б) содержащих, тригонометрические функции с) имеющих, вид 1. Подставить предельное значение аргумента в исследуемое выражение. Если при этом получено конечное значение, то оно является пределом данной функции. 2. Определить тип неопределенности:
Пояснение: а) если функция является дробно- рациональной (сл. а), то далее выполняются пункты 3,4,5 алгоритма. б) если функция содержит тригонометрические выражения, а неопределенность типа с) если выражение представляет неопределенность типа 3. Выписать старшую степень числителя и знаменателя 4. Поделить числитель и знаменатель функции на 5. Найти предел полученного выражения. 6. Заменить данное выражение эквивалентным ему более простым выражением, используя таблицу эквивалентных бесконечно- малых (следствие из 1 замечательного предела): 7. Найти предел эквивалентного выражения. 8. Преобразовать выражение к виду, позволяющему использовать 2 замечательный предел.
Пример 1. Найти Решение.
Пояснение. Непосредственно теорему о пределе дроби применить нельзя, так как числитель и знаменатель дроби при х→∞ не имеют конечных пределов. Имеем неопределенность вида ∞/∞. Для раскрытия ее разделим числитель и знаменатель на х в наивысшей степени, т.е. на х4. Получим функции Вообще предел отношения двух многочленов при
Пример 2. Найти Решение. Здесь имеется неопределенность вида 0/0. Дня ее раскрытия умножим числитель и знаменатель на сопряжённый множитель:
Пример 3. Найти Решение. Вычислим: 1) Представим Пусть 2) 3) Пример 4. Найти Решение. Вычислим: Воспользуемся 1-ым замечательным пределом.
а) Раскрытие неопределенности Алгоритм: 1) убедимся, что при 2) определим наивысшую степень 3) разделим числитель и знаменатель дроби на 4) заметим, что 5)что бы получить окончательный результат, воспользуемся теоремами о пределах суммы, произведения, частного. б) Раскрытие неопределенности Алгоритм: 1) убедимся, что при 2) числитель и знаменатель дробно рациональной функции, стоящей под знаком предела, разложим на множители по формуле 3) полученную после разложению на сомножители дробно рациональную функцию, сократим на 4) убедимся, что под знаком предела получена функция непрерывная в точке 5) вычислим предел в точке Выберите свой вариант и решите задачу.
Задание 13. Вычисление производной функции. Алгоритм решения 1) выделим маркером или подчеркнем правила дифференцирования, приведенные ниже, необходимые для решения примера:
2) выражения с радикалами, если они присутствуют в примере, представим в виде степени, воспользовавшись формулой 3) воспользуемся теоремой: производная сложной функции 4) выделим маркером или подчеркнем формулы из таблицы производных, приведенной ниже, необходимые для решения примера: Выберите свой вариант и решите задачу.
Задание 14.Вычисление неопределенного интеграла с помощью замены переменной.
Алгоритм: 1. Выполним замену переменной под знаком интеграла, воспользовавшись, указанной в примере подстановкой и формулой дифференциала функции: (например, если 2. Подчеркнем или выделим маркером соответствующий полученному решению табличный интеграл; для нахождения неопределенного интеграла, воспользуемся выделенной формулой; под знаком интеграла выполним обратную замену, т.е. выразим
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 2759; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.159.223 (0.009 с.) |

 , где
, где 
 . Заметим, что
. Заметим, что  и
и  не являются неопределенностью, в первом случае предел равен нулю, во втором -
не являются неопределенностью, в первом случае предел равен нулю, во втором -  .
. (сл. б), то далее выполняются пункты 6,7 алгоритма.
(сл. б), то далее выполняются пункты 6,7 алгоритма. (сл. с), выполняется пункт 8.
(сл. с), выполняется пункт 8. , если функция представляет собой дробно - рациональную и получена неопределенность типа
, если функция представляет собой дробно - рациональную и получена неопределенность типа  .
. .
.











 (неопределённость)
(неопределённость)





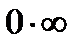 (неопределённость)
(неопределённость)

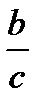

 (неопределённость)
(неопределённость)

 (неопределённость)
(неопределённость)





 (неопределённость)
(неопределённость)
 (неопределённость)
(неопределённость)
 (неопределённость)
(неопределённость)








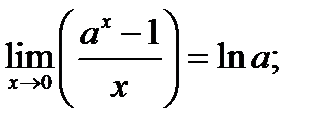

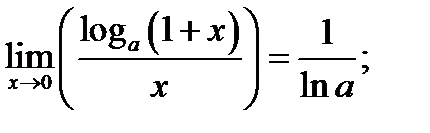



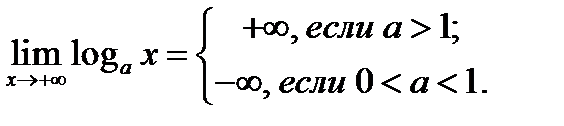

 .
.
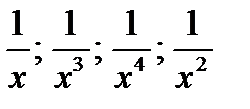 , которые являются бесконечно малыми при х → ∞, и поэтому их пределы равны нулю.
, которые являются бесконечно малыми при х → ∞, и поэтому их пределы равны нулю. :
:
 .
. , тогда в числителе получим разность квадратов:
, тогда в числителе получим разность квадратов:  и при х-1≠0 дробь становится сократимой и имеющая смысл при х=1. Таким образом,
и при х-1≠0 дробь становится сократимой и имеющая смысл при х=1. Таким образом,

 .
.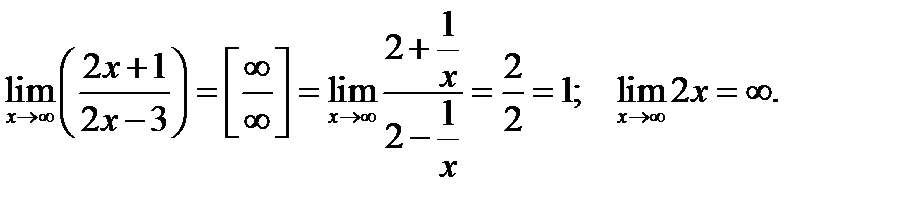 Убедившись, что при
Убедившись, что при 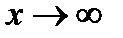 функция, представляет степень, основание которой стремится к единице, а показатель к бесконечности (случай
функция, представляет степень, основание которой стремится к единице, а показатель к бесконечности (случай 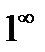 ), далее преобразуем функцию так, чтобы использовать 2-ой замечательный предел.
), далее преобразуем функцию так, чтобы использовать 2-ой замечательный предел. в виде
в виде  .
. Итак,
Итак, 
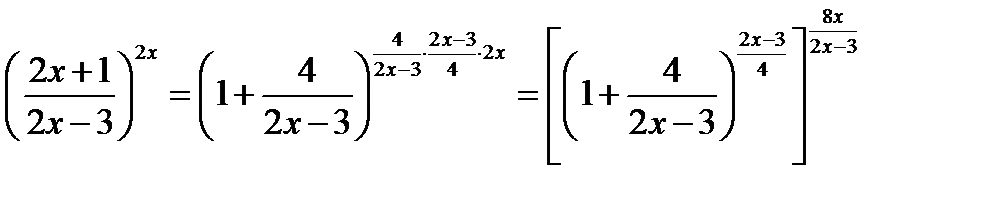 .
.
 .
. , т.е. неопределённость типа
, т.е. неопределённость типа  .
.
 при вычислении предела в дробно рациональной функции.
при вычислении предела в дробно рациональной функции. имеет место случай
имеет место случай  переменной
переменной  , присутствующую в дробно рациональной функции;
, присутствующую в дробно рациональной функции; ;
; при
при 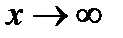 , являются бесконечно малыми;
, являются бесконечно малыми; при вычислении предела в дробно рациональной функции.
при вычислении предела в дробно рациональной функции. имеет место неопределенность вида
имеет место неопределенность вида  (в этом случае
(в этом случае  будет корнем каждого из квадратных трехчленов в числителе и знаменателе);
будет корнем каждого из квадратных трехчленов в числителе и знаменателе);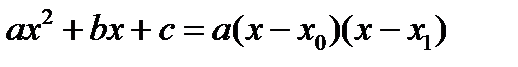 ;
; ;
; б)
б) 
 ;
б)
;
б) 
 б).
б). 
 ;
б).
;
б). 
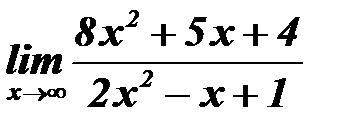 ;
б)
;
б)  ;
б)
;
б)  ;
б)
;
б)  ;
б)
;
б) 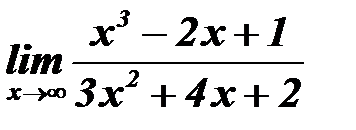 ;
б)
;
б)  ;
б)
;
б)  , где
, где 
 ,где
,где 
 , где
, где 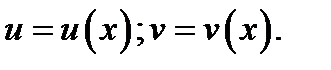
 , где
, где  ;
; 
 , где
, где 
 , где
, где 



 , где
, где 

 , где
, где 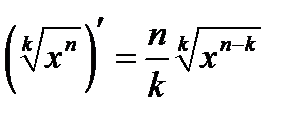
 , где
, где 
 , где
, где 
 , где
, где 
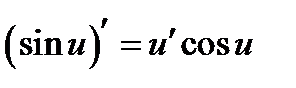 , где
, где 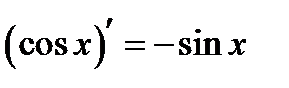
 , где
, где 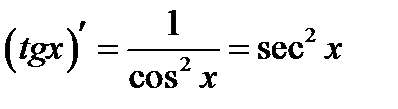
 , где
, где 
 , где
, где 
 , где
, где 
 , где
, где 
 , где
, где 
 , где
, где 
 , где
, где 
 , где
, где 
 , где
, где 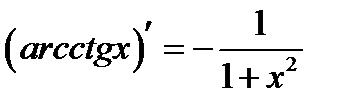
 , где
, где  ;
;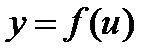 , где
, где  , равна произведению ее производной по промежуточному аргументу
, равна произведению ее производной по промежуточному аргументу  на производную этого аргумента по независимой переменной
на производную этого аргумента по независимой переменной 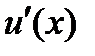 , т.е.
, т.е. 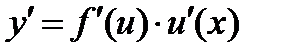 ;
;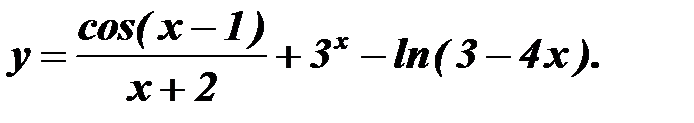




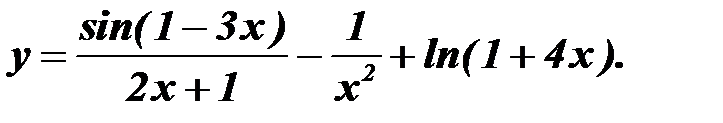
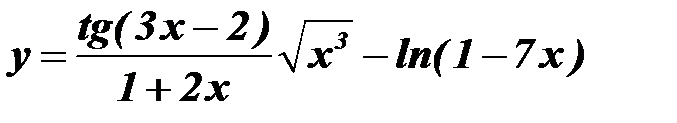

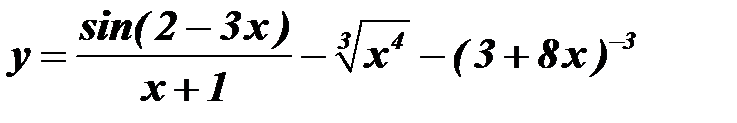


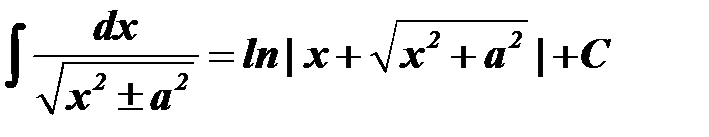
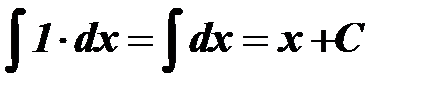










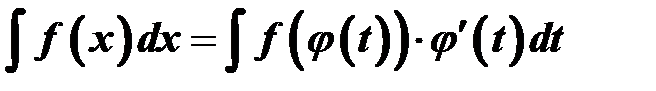 ;
; 

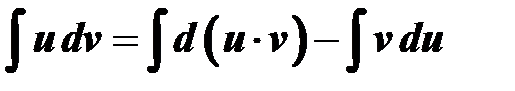







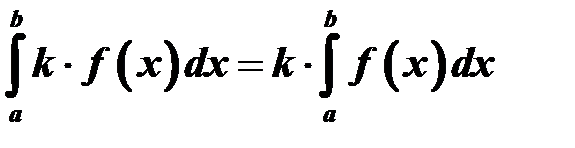
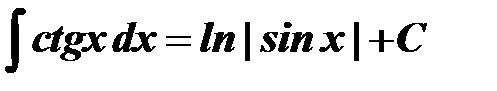
























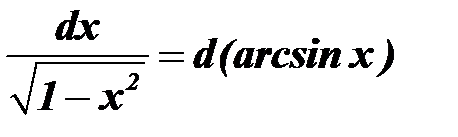


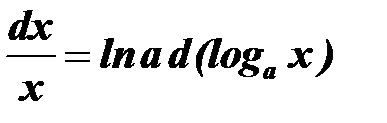



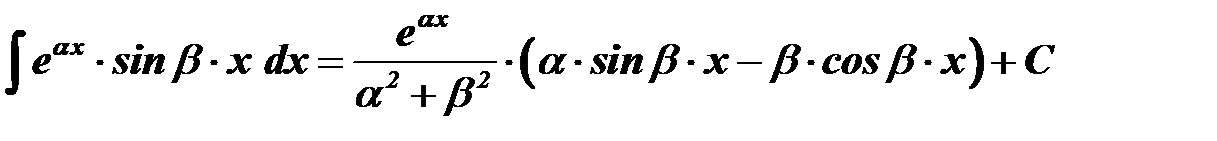


 , то
, то  ); в результате преобразований будет получен один из табличных интегралов, приведенных ниже.
); в результате преобразований будет получен один из табличных интегралов, приведенных ниже. через переменную
через переменную 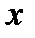 .
.


