Алгоритм Сазерленда-Ходгмана

Простой метод решения проблемы охвата отсекаемым многоугольником вершины окна предлагается в алгоритме Сазерленда-Хогдмана [40], когда весь многоугольник последовательно отсекается каждой границей окна, как это показано на рис. 0.3.23.

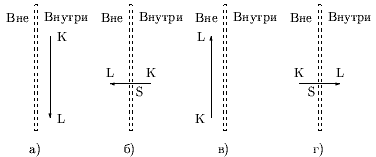
При отсечении ребра, соединяющего очередную пару вершин K и L, возможны 4 случая взаимного расположения (рис. 0.3.24):

а) ребро на внутренней стороне границы,

б) ребро выходит из окна наружу,

в) ребро на внешней стороне границы,

г) ребро входит снаружи в окно.

Рис. 0.3.22: Относительные расположения ребра и границы окна.

В случае а) в результат добавляется вершина L. В случае б) в результат заносится S - точка пересечения ребра с границей. В случае в) нет вывода. В случае г) выдаются точка пересечения S и конечная точка ребра L.

Для определения взаимного расположения и направленности используется векторное произведение вектора P ₁ P ₂, проведенного из начальной в конечную точку текущего ребра окна, на вектор P ₁ S из начальной точки текущего ребра окна в очередную вершину S многоугольника (рис. 0.3.25).

Если P ₁ P ₂ × P ₁ S < 0, то поворот от P ₁ P ₂ к P ₁ S по часовой стрелке, т.е. точка S внутри окна.
Если P ₁ P ₂ × P ₁ S > 0, то поворот от P ₁ P ₂ к P ₁ S против часовой стрелки, т.е. точка S вне окна.

Простой алгоритм отсечения многоугольника

В данном разделе рассматривается простой алгоритм отсечения, который подобно алгоритму Сазерленда-Ходгмана может генерировать лишние стороны для отсеченного многоугольника, проходящие вдоль ребра окна отсечения. Но этот алгоритм несколько более быстрый и использует те же подпрограммы обработки многоугольного окна отсечения, что и алгоритм Кируса-Бека. Многоугольник отсекается одним ребром выпуклого окна отсечения. В результате такого отсечения формируется новый многоугольник, который затем отсекается следующим ребром и т.д., пока не будет выполнено отсечение последним ребром окна. Основная здесь процедура - процедура отсечения отдельным ребром, определяющая взаимное расположение очередной стороны многоугольника и ребра отсекателя и генерирующая соответствующие выходные данные.

Алгоритм отсечения многоугольника Вейлера-Азертона

1. Строятся списки вершин отсекаемого многоугольника и окна.
2. Отыскиваются все точки пересечения. При этом расчете касания не считаются пересечением, т.е. когда вершина или ребро отсекаемого многоугольника инцидентна или совпадает со стороной окна (рис. 0.3.29 и 0.3.30).
3. Списки координат вершин отсекаемого многоугольника и окна дополняются новыми вершинами - координатами точек пересечения. Причем если точка пересечения Pk находится на ребре, соединяющем вершины Vi, Vj, то последовательность точек Vi, Vj превращается в последовательность Vi, Pk, Vj. При этом устанавливаются двухсторонние связи между одноименными точками пересечения в списках вершин отсекаемого многоугольника и окна.
   Входные и выходные точки пересечения образуют отдельные подсписки входных и выходных точек в списках вершин.
4. Определение части обрабатываемого многоугольника, попавшей в окно выполняется следующим образом:
   Если не исчерпан список входных точек пересечения, то выбираем очередную входную точку.
   Двигаемся по вершинам отсекаемого многоугольника пока не обнаружится следующая точка пересечения; все пройденные точки, не включая прервавшую просмотр, заносим в результат; используя двухстороннюю связь точек пересечения, переключаемся на просмотр списка вершин окна.
   Двигаемся по вершинам окна до обнаружения следующей точки пересечения; все пройденные точки, не включая последнюю, прервавшую просмотр, заносим в результат.
   Используя двухстороннюю связь точек пересечения, переключаемся на список вершин обрабатываемого многоугольника.
   Эти действия повторяем пока не будет достигнута исходная вершина - очередная часть отсекаемого многоугольника, попавшая в окно, замкнулась. Переходим на выбор следующей входной точки в списке отсекаемого многоугольника.

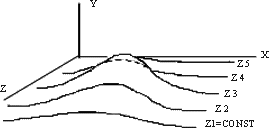
Алгоритмы удаления невидимых линий и поверхностей. Алгоритм плавающего горизонта. Другие методы удаления невидимых линий к поверхностей: алгоритм Варнока, алгоритм Вейлера-Азертона, алгоритм разбиения криволинейных поверхностей.

Алгоритм плавающего горизонта чаше всего используется для удаления невидимых линий трех­мерного представления функций, описывающих по­верхность в виде:

F(x, у, z) = 0

Подобные функции возникают во многих приложениях в математике, технике, естественных науках и других дисциплинах.

Главная идея данного метода заключается в сведении трехмерной задачи к двумерной путем пересечения ис­ходной поверхности последовательностью параллельных секущих плоскостей, имеющих постоянные значения координат х, у или z.

На рис. 5.2 приведен пример, где указанные параллельные плоскости определяются по­стоянными значениями z. Функция F(x,у,z) = 0 сводится к последовательности кривых, лежащих в каждой из этих параллельных плоско­стей, например к последовательности у = f(x,z) или х=g(у,z), где z постоянно на каждой из заданных параллельных плоскостей.

Рис. 4.2 Секущие плоскости с постоянной координатой

Рис. 4.3 Секущие плоскости с постоянной координатой

Итак, поверхность теперь складывается из последовательности кривых, лежащих в каж­дой из этих плоскостей, как показано на рис. 5.3. Здесь предполагается, что полученные кривые являются однозначными функциями не­зависимых переменных. Если спроецировать полученные кривые на плоскость z = 0, как показано на рис. 5.4, то сразу становится ясна идея алгоритма удаления невидимых участков исходной поверхности.

 

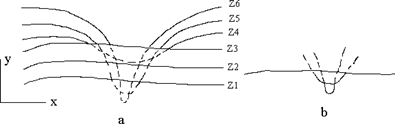
Рис. 4.4 Проекция кривых на плоскость z = 0

Алгоритм сначала упорядочивает плоскости z = const по возрастанию расстояния до них от точки наблюдения. Затем для каждой плоскости, начиная с ближайшей к точке наблюдения, строится кривая, лежащая на ней, т. е. для каждого значения координаты х в пространстве изображения определяется соответствующее значение y. Ал­горитм удале­ния невидимой линии заключается в следующем:

Если на текущей плоскости при некотором заданном значении x соответствующее зна­чение у на кривой больше значения y для всех предыдущих кривых при этом значении x, то текущая кривая видима в этой точке; в против­ном случае она невидима.

Невидимые участки показаны пунктиром на рис. 5.4. Реализация данного алгоритма достаточно проста. Для хранения максимальных значений y при каждом значении x ис­пользуется массив, длина которого равна числу различимых точек (разрешению) по оси x в пространстве изображения. Значения, хранящиеся в этом массиве, представляют собой текущие значения "горизонта". Поэтому по мере рисования каждой очередной кривой этот горизонт "всплывает". Фактически этот алгоритм удаления невидимых линий рабо­тает каждый раз с одной ли­нией.

Алгоритм работает очень хорошо до тех пор, пока какая-нибудь очередная кривая не окажется ниже самой пер­вой из кривых, как показано на рис. 5.5а.

 

Рис. 4.5 Обработка нижней стороны поверхности

Подобные кривые, естественно, видимы и представляют собой нижнюю сторону исход­ной поверхности, однако алгоритм будет считать их невидимыми. Нижняя сторона по­верхности делается видимой, если модифицировать этот алгоритм, включив в него ниж­ний горизонт, который опускается вниз по ходу работы алгоритма. Это реали­зуется при помощи второго массива, длина которого равна числу различимых точек по оси x в про­странстве изо­бражения. Этот массив содержит наименьшие значения y для каждого зна­чения x. Алгоритм теперь становится таким:

Если на текущей плоскости при некотором заданном значении x соответствующее зна­чение y на кривой больше максимума или меньше минимума по y для всех предыдущих кривых при этом x, то текущая кривая видима. В противном случае она невидима.

Полученный результат показан на рис. 5.5b.

В изложенном алгоритме предполагается, что значение функции, т.е. y, известно для каждого значения x в про­странстве изображения. Однако если для каждого значениях нельзя указать (вычислить) соответствующее ему значение y, то невозможно поддерживать массивы верхнего и нижнего плавающих горизонтов. В таком случае ис­пользуется линейная интерполяция значений y между известными значениями для того, чтобы заполнить мас­сивы верхнего и нижнего плавающих горизонтов.

Алгоритмы удаления невидимых линий и поверхностей. Алгоритм, использующий z-буфер. Другие методы удаления невидимых линий и поверхностей: алгоритмы, использующие список приоритетов, алгоритмы построчного сканирования.

Это один из простейших алгоритмов удаления невидимых поверхностей. Впервые он был предложен Кэтмулом. Работает этот алгоритм в пространстве изображения. Идея z -буфера является простым обобщением идеи о бу­фере кадра. Буфер кадра используется для запоминания атрибутов (интенсивности) каждого пиксела в простран­стве изображения, z -буфер - это отдельный буфер глубины, используемый для запоминания координаты z или глубины каждого видимого пиксела в пространстве изображения. В процессе работы глубина или значение z ка­ждого нового пиксела, который нужно зане­сти в буфер кадра, сравнивается с глубиной того пиксела, который уже занесен в z -бу­фер. Если это сравнение показывает, что новый пиксел расположен впереди пиксела, на­ходя­щегося в буфере кадра, то новый пиксел заносится в этот буфер и, кроме того, про­изводится корректировка z -бу­фера новым значением z. Если же сравнение дает противоположный результат, то никаких действий не произво­дится. По сути, алгоритм является поиском по х и у наибольшего значения функции z (х, у).

Главное преимущество алгоритма - его простота. Кроме того, этот алгоритм решает за­дачу об удалении неви­димых поверхностей и делает тривиальной визуализацию пересе­чений сложных поверхностей. Сцены могут быть любой сложности. Поскольку габариты пространства изображения фиксированы, оценка вычислительной трудо­емкости алго­ритма не более чем линейна. Поскольку элементы сцены или картинки можно заносить в буфер кадра или в z -буфер в произвольном порядке, их не нужно предварительно сорти­ровать по приоритету глубины. Поэтому экономится вычислительное время, затрачивае­мое на сортировку по глубине.

Основной недостаток алгоритма - большой объем требуемой памяти. Если сцена под­вергается видовому преоб­разованию и отсекается до фиксированного диапазона коорди­нат z значений, то можно использовать z -буфер с фиксированной точностью. Информацию о глубине нужно обрабатывать с большей точностью, чем координатную информацию на плоскости (х, y); обычно бывает достаточно 20 бит. Буфер кадра разме­ром 512х512х24 бит в комбинации с z -буфером размером 512х512х20 бит требует почти 1.5 мегабайт памяти. Однако снижение цен на память делает экономически оправданным создание специализированных запоминающих уст­ройств для z -буфера и связанной с ним аппаратуры.

Другой недостаток алгоритма z-буфера состоит в трудоемкости и высокой стоимости устранения лестничного эффекта, а также реализации эффектов прозрачности и просве­чивания. Поскольку алгоритм заносит пикселы в буфер кадра в произвольном порядке, то нелегко получить информацию, необходимую для методов устранения лестничного эффекта, основывающихся на предварительной фильтрации. При реализации эффектов прозрачности и просвечивания, пикселы могут заноситься в буфер кадра в некорректном порядке, что ведет к ло­кальным ошибкам.

Формальное описание алгоритма z-буфера таково:

1. Заполнить буфер кадра фоновым значением интенсивности или цвета.

2. Заполнить z -буфер минимальным значением z.

3. Преобразовать каждый многоугольник в растровую форму в произвольном по­рядке.

4. Для каждого Пиксел(x,y) в многоугольнике вычислить его глубину z (x,y).

5. Сравнить глубину z (х,у) со значением Zбуфер(х,у), хранящимся в z -буфере в этой же позиции.

Если z (х, у) > Zбуфер (х,у), то записать атрибут этого многоугольника (интенсивность, цвет и т. п.) в буфер кадра и заменить Zбуфер(х,у) на z (х,у). В противном случае никаких действий не производить.