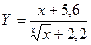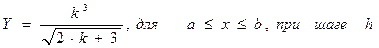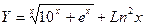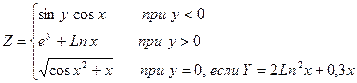Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составление простейших алгоритмов обработки одномерных массивовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Подсчитать количество отрицательных элементов в числовом массиве Z, состоящем из N чисел. Вывести массив отрицательных чисел в строку. 2. Определить сумму отрицательных чисел среди элементов одномерного числового массива, состоящего из N чисел, отрицательные элементы массива вывести в столбик в обратном порядке. 3. Найти наименьшее число среди К элементов одномерного числового массива. Вывести массив в строку, в столбик. 4. В одномерном числовом массиве X, состоящем из N элементов, подсчитать количество элементов, квадрат которых больше 100, но меньше 200. Вывести квадраты этих элементов. 5. Найти произведение положительных элементов одномерного числового массива, состоящего из N чисел. Вывести положительные элементы в обратном порядке. 6. В одномерном числовом массиве, состоящем из N элементов, заменить все отрицательные числа нулями и подсчитать их количество. Вывести элементы массива на экран. 7. В одномерном числовом массиве определить произведение чисел, меньших 18. Вывести элементы массива в обратном порядке в столбик. 8. В одномерном числовом массиве, состоящем из N элементов, заменить все отрицательные числа их квадратами и подсчитать их количество. Вывести оба массива. 9. Из одномерного числового массива X, состоящего из N элементов, выбрать элементы, квадрат которых не меньше 100 и подсчитать их произведение. Вывести новый массив в столбик. 10. Определить в одномерном числовом массиве, состоящем из N элементов, наибольшее число. Вывести исходный массив на экран в строку. 11. В одномерном числовом массиве, состоящем из N элементов, определить количество чисел, квадрат которых превышает 100, и заменить их нулями. Вывести оба массива в две строки. 12. В одномерном числовом массиве, размер которого неизвестен, заменить все отрицательные элементы нулями и вывести их на экран в столбик. 13. Определить количество целых чисел среди К элементов одномерного числового массива и заменить их нулями. Вывести на экран элементы нового массива в строку в обратном порядке. 14. В одномерном числовом массиве, размер которого неизвестен, заменить все числа, кратные А, единицей. Подсчитать их количество и вывести на экран оба массива. 15. Определить количество дробных чисел среди К элементов одномерного числового массива. Элементы исходного массива вывести на экран. 16. В одномерном числовом массиве заменить все отрицательные числа их квадратами и подсчитать их количество. Новый массив вывести на экран в строку в обратном порядке. 17. В одномерном числовом массиве P, состоящем из N элементов, заменить все числа, меньшие заданного числа А, единицей. Подсчитать их произведение и вывести на экран оба массива в две строки. 18. В одномерном числовом массиве K, состоящем из N элементов, заменить все отрицательные элементы их модулями. Исходный массив вывести в строку в прямом порядке, а полученный – в строку, в обратном порядке. 19. Определить сумму отрицательных чисел среди элементов одномерного числового массива, состоящего из N чисел, отрицательные элементы массива вывести в столбик в обратном порядке. 20. В одномерном числовом массиве, состоящем из N элементов, определить количество чисел, квадрат которых превышает 100, и заменить их нулями. Вывести оба массива в две строки. 21. Подсчитать в одномерном числовом массиве, состоящем из N чисел, сумму синусов последних 10 элементов. Вывести синусы этих элементов на экран в 2 столбца. 22. В одномерном числовом массиве определить сумму чисел, меньших 25. Вывести элементы массива в обратном порядке в строку. 23. В одномерном числовом массиве определить количество чисел, меньших 25. Вывести элементы массива в обратном порядке в столбец. 24. В одномерном числовом массиве, состоящем из N элементов, определить сумму чисел, квадрат которых превышает 100, и заменить их единицами. Вывести оба массива в две строки. 25. Определить произведение целых чисел среди К элементов одномерного числового массива и заменить их нулями. Вывести на экран элементы исходного и нового массивов в строку.
Решение циклических задач с использованием характерных приемов
По заданным вещественным значениям a, b и целому N получить: - значения yi = f (a, b, i), где i = 1,2,.., N, f – заданная функция; - значения U = G (y1, y2, …, yN), где G – заданная функция. Варианты функции f (a, b, i): ì (i + 1)×(2×a + b×i) ì (a - b×i) 4 | ---------------------, a > b | --------------------, b > 1 ç (b - a) 2 + a×i + i2 | i×(a2 + 3×b×i + 4×i2) 1) f = í 2) f = í ï (i - 1)×(2×b + a×i) | (a + b×i) 4 ï -----------------------, a £ b | -------------------------, b £ 1 î 9×(b - a) 2 + a×i + i2 î i×(a2 + 3×(1-b)×i + 4i2) ì (a + (-1)i×b×i) 2 ì i×a2 + (-1)i+1×i2×(b - a) ½ ----------------, b > 0 ½ --------------------------, a > 0 ½ i×(i + b2) 0.5 ½ (5×a2 + a×i + b2×i2) 0.5 3) f = í 4) f = í ½ (a + b×i) 2 ½ i×a2 + i2×(b - a) ½ --------------, b £ 0 ½ -----------------------, a £ 0 î i× (i + b2) 0.5 î (5×a2 – a×i + b2×i2) 0.5 ì 2×a×i2 – b×i + 3×a×b ½ ----------------------, a > b ì ½ (a2 + 4b2 + i2)0.5 ½ i×a2 - (i + b2)/(i + a2), a > b 5) f = í 6) f = í ½ i×a2 + 1 ½ (i×a2 + b/i)2, a £ b ½ -----------, a £ b î î a - b + i ì 2×(a×b)2 + i2 - a | ------------------, |a×b| £ 1 ì | 2× (a2 + b2) + i | [a+b+i+ (-1)i×(b - a)]/(a×i)0.5, a > 0 7) f = í 8) f = í | 2×a×b + (-1)i×(a-i) | |a + i| + |b - i|, a £ 0 | --------------------, |a×b| > 1 î î 2×(a2 + b2) ì (a - i)2 + (b + i)2 ì (a×i + 2×b)2 + (-1)i×i | -------------------, a £ b | ------------------------, a > 0 | (a2 + 2×b2 + i2)0.5 | (i2 + i)0.5 9) f = í 10) f = í | (a + i)2 + (b - i)2 | (a×i + 2×b)2 + i | ------------------------, a > b | -----------------, a £ 0 î (a2 - (-1)i×b2 + i2)0.5 î (i2 – i + 1)0.5 Варианты функции U = G (y 1, y2, …, yN): 1) G = min [(yi2+a2)/2]0.5 2) G = min [|yi2+a2|/(a2+b2)] 1£ i£N 1£ i£N ì yi, |yi|£2 3) G=0.5(max |yi|2 + min |yi|2) 4) G = max |zi|, где zi = í 1£ i£N 1£ i£N 1£ i£N î 0.5, | yi|>2 ì yi, |yi|>1 N ì yi, yi Ì (0,10) 5) G = max |zi|, zi =í 6) G = å zi, zi = í 1£ i£N î 2, |yi|£1 i=1 î 1, yi Ë(0,10) N ì yi, yiÌ(0,15) N ì yi, |yi|£1 7) G = å (zi0.5- zi) 2, zi = í 8) G =å zi2, zi = í i=1 î 2, yi Ë(0,15 i=1 î 1/yi, |yi|>1 N ì yi, |yi|£10 N ìmax(yi,10-yi), yi Ì(0,10) 9) G = å(10+zi) 0.5, zi=í 10) G =å zi, zi = í i=1 î 0, |yi|>10 i=1 î 5, yiË (0,10) Задание 6. Составление алгоритмов и программ обработки Двумерных массивов
Дана матрица
1. Найти сумму элементов по каждой строке матрицы 2. Найти максимальный по модулю элемент матрицы 3. Найти сумму элементов по каждому столбцу матрицы 4. Найти максимальные элементы в столбцах матрицы 5. Найти максимальный элемент матрицы 6. Найти номера строк, где находятся максимальные элементы в столбцах матрицы 7. В матрице 8. В матрице 9. В матрице 10. В матрице 11. Найти средние арифметические значения положительных элементов каждой строки матрицы 12. В матрице 13. В матрице 14. В матрице 15. В матрице 16. В матрице 17. Для положительных элементов главной диагонали матрицы 18. Для отрицательных элементов главной диагонали матрицы 19. В матрице 20. В матрице
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 1. Задан одномерный массив X размерности N. Вычислить значение функции Z = g(X) в соответствии с предложенными алгоритмами: N N 1) å (Xi × XN-i+1); 2) Õ (Xi + XN-i+1); 3) max (|Xi+1| - |Xi|); i=1 i=1 1£ i£N-1 4) (X1 + X2 +X3)×X2 + (X2 + X3 +X4)×X3 + … +(XN-2 + XN-1 +XN)×XN-1
5) (1 + å Xi) / (2 + å Xi); 6) max { |Xi| }; 7) (|X1×X2 ×X3 × …× XN|)0.5 Xi £1 Xi >1 1£ i£N N 8) Õ (1 / |Xi +1| + Xi+1); 9) max{Xi} - min{Xi}; 10) max{Xi–2.5}0.5 i=1 1£ i£N 1£ i£N 1£ i£N 2. Выполнить указанное преобразование над элементами массивов:
1. В массиве A(N) расположите элементы в порядке возрастания. 2. В массиве B(N) поменяйте местами первый и последний элементы. 3. В массиве A(N) расположите элементы в порядке убывания. 4. В массиве B(N) поменяйте местами второй и предпоследний элементы. 5. В массиве A(N) расположите элементы так, чтобы отрицательные были в конце. 6. В массиве B(N) поменяйте местами первый отрицательный и максимальный элементы. 7. В массиве A(N) расположите элементы так, чтобы положительные были в конце. 8. В массиве A(N) поменяйте местами первый положительный и минимальный элементы. 9. В массиве B(N) увеличьте все элементы массива на 4. 10. В массиве А(N) уменьшите все элементы массива на 4. 11. В массив A(N) вставьте первый элемент, равный 7. 12. В массив В(N) вставьте последний элемент, равный 7. 13. Из массива A(N) сформируйте два массива, один из массивов будет заполнен положительными, а второй – отрицательными элементами. 14. В массиве B(N) увеличьте все элементы массива в 5 раз. 15. В массив A(N) вставьте пятый элемент, равный 8. 16. Из массива A(N) сформируйте два массива, один из массивов будет заполнен предшествующими максимальному элементу, а второй – остальными элементами. 17. В массиве B(N) уменьшите все элементы массива в 10 раз. 18. Дан двухмерный массив А из 5 строк и 7 столбцов. Найти среднее арифметическое значение элементов массива. 19. Дан двумерный массив А из 4 строк и 6 столбцов. Найти сумму элементов, стоящих в пятом столбце. 20. Дан двумерный массив А из 6 строк и 7 столбцов. Найти произведение элементов, стоящих в строках с нечетным индексом. 21. Дан двумерный массив А из 4 строк и 5 столбцов. Найти сумму элементов, индексы которых в сумме составляют К. 22. Дан массив А (4, 5). Найти максимальный по абсолютному значению элемент массива и вывести его на печать. 23. Дан массив А (N, N). Найти сумму элементов, стоящих на главной диагонали массива. 24. Дан массив A(N, N). Найти сумму элементов, стоящих на побочной диагонали массива. 25. В массиве А (N, N) определить произведение положительных элементов ниже главной диагонали. 26. В массиве A (N, N) подсчитать количество нулевых элементов, расположенных выше главной диагонали. 27. Дан массив A (N,N). Найти максимальный элемент побочной диагонали. 28. Определить сумму элементов квадратной матрицы A (N, N), расположенной в левой четверти, ограниченной диагоналями, включая диагональные элементы. ОПИСАНИЕ МНОЖЕСТВ
На плоскости заданы N точек с координатами (Xi, Yi) (i = Для облегчения составления программы и дальнейшего контроля правильности решения необходимо в отчете к лабораторной работе привести графическое изображение заданного множества. 1. Координаты точек для вариантов № 1–15.
2. Координаты точек для вариантов № 16–25
3. Описание множества D: 1. Круг радиусом R = 7 с центром в точке А (–0,3; –3,4) делится прямыми Y = X, Y = – X на 4 части. D – «верхняя» часть круга. 2. Круг радиусом R = 2 с центром в точке А (–0,3; –3,4) делится прямыми Y = X –2, Y =- X –2 на 4 части. D – «правая» часть круга. 3. D – круг радиусом R = 2 с центром в точке А (2,2). 4. D – внутренность квадрата со стороной H = 3 и с центром в точке А(1,1) со сторонами, параллельными координатным осям. 5. Множество D заключено между сторонами двух квадратов с общим центром в точке А (2,2), стороны которых Н 1 = 2 и Н 2 = 4 параллельны осям координат. 6. D – общая часть кругов, радиусы которых R 1 = 2, R 2 = 1,5 и центры расположены соответственно в точках А(0,1) и В(–2,1). 7. D – часть круга радиусом R 1 = 2 c центром в точке А(0,1), лежащая вне круга радиусом R 2 = 1,5 с центром в точке В(–2,1). 8. D – объединения кругов радиусами R 1 = 2 и R 2 = 1,5 с центрами соответственно в точках А(0,1) и В(–2,1). 9. D – внешность круга радиусом R = 2 с центром в точке А(2,2). 10. D – внешность квадрата с центром в точке А(2,2), стороны которого Н = 2 параллельны координатным осям. 11. Круг радиусом R = 1,5 с центром в точке А (2,2) пересекается прямой Х = 1,7. D – часть круга, лежащая справа от секущей. 12. Круг радиусом R = 1,5 с центром в точке А (2,2) пересекается прямой Y = 1,6. D – часть круга, лежащая над секущей. 13. Круг радиусом R = 1,5 с центром в точке А(2,2) пересекается прямыми Y = 1,2 и Y = 2,15. D – часть круга, лежащая между секущими. 14. Круг радиусом R = 1,5 с центром в точке А(2,2) пересекается прямыми Х = 3, Х = 0,8. D – часть круга лежащая между секущими. 15. Круг радиусом R =1,5 с центром в точке А(2,2) пересекается прямыми Y = 1,2 и Х = 1. D – правая верхняя часть круга. 16. Круг радиусом R = 1,5 с центром в точке А(2,2) пересекается прямыми Y = 2,3 и Х = 1,9. D – левая верхняя часть круга. 17. Круг радиусом R = 1,5 с центром в точке А(2,2) пересекается прямыми Y = 3 и Х = 1. D – правая нижняя часть круга. 18. Круг радиусом R = 1,5 с центром в точке А(2,2) пересекается прямыми Y = 2,5 и Х = 2,7. D – левая нижняя часть круга. 19. D – окружность радиусом R = 2 с центром в точке А(2,2). 20. D – граница квадрата со стороной Н = 2 и центром А(2,2). Стороны квадрата параллельны осям координат. 21. D – кольцо, заключенное между окружностями радиусов R 1 = 1,5 и R 2 = 2, имеющими общий центр в точке А(2,2). 22. D – часть круга радиусом R = 1,5 с центром в точке А(2,2), лежащая под прямой Y = Х. 23. D – пересечение (общая часть) круга радиусом R = 2 с центром в точке А(0,1) и квадрата со стороной Н = 1,5 и центром в точке В(-2,1). Стороны квадрата параллельны осям координат. 24. D – часть круга радиусом R = 2 с центром в точке А(0,1) лежащая вне квадрата со стороной Н = 1,5 и центром в точке В(-2,1). Стороны квадрата параллельны осям координат.
КОНТРОЛЬНАЯ РАБОТА №1 Вариант 1 1.Вычислить и вывести на экран значение функции
2. Произвести вычисление значения функции Z. Предусмотреть вывод на экран значения X и вычисленных значений Y и Z.
3.Табулирование функции на интервале с заданным шагом. Предусмотреть вывод на экран в виде таблицы значений аргумента X и вычисленных значений Y.
Вариант 2 1.Вычислить и вывести на экран значение функции
2. Произвести вычисление значения функции Z. Предусмотреть вывод на экран значения X и вычисленных значений Y и Z.
3.Табулирование функции на интервале с заданным шагом. Предусмотреть вывод на экран в виде таблицы значений аргумента X и вычисленных значений Y.
Вариант 3 1.Вычислить и вывести на экран значение функции
2. Произвести вычисление значения функции Z. Предусмотреть вывод на экран значения X и вычисленных значений Y и Z.
3.Табулирование функции на интервале с заданным шагом. Предусмотреть вывод на экран в виде таблицы значений аргумента X и вычисленных значений Y.
Вариант 4 1.Вычислить и вывести на экран значение функции
2. Произвести вычисление значения функции Z. Предусмотреть вывод на экран значения X и вычисленных значений Y и Z.
3.Табулирование функции на интервале с заданным шагом. Предусмотреть вывод на экран в виде таблицы значений аргумента X и вычисленных значений Y.
Вариант 5 1.Вычислить и вывести на экран значение функции
2. Произвести вычисление значения функции Z. Предусмотреть вывод на экран значения X и вычисленных значений Y и Z.
3.Табулирование функции на интервале с заданным шагом. Предусмотреть вывод на экран в виде таблицы значений аргумента X и вычисленных значений Y.
Вариант 6 1.Вычислить и вывести на экран значение функции
2. Произвести вычисление значения функции Z. Предусмотреть вывод на экран значения X и вычисленных значений Y и Z.
3.Табулирование функции на интервале с заданным шагом. Предусмотреть вывод на экран в виде таблицы значений аргумента X и вычисленных значений Y.
Вариант 7 1.С помощью компьютера вычислить и вывести на экран значение функции
2. Произвести вычисление значения функции Z. Предусмотреть вывод на экран значения X и вычисленных значений Y и Z.
3.Табулирование функции на интервале с заданным шагом. Предусмотреть вывод на экран в виде таблицы значений аргумента k и вычисленных значений Z.
Вариант 8 1.Вычислить и вывести на экран значение функции
2. Произвести вычисление значения функции Z. Предусмотреть вывод на экран значения X и вычисленных значений Y и Z.
3.Табулирование функции на интервале с заданным шагом. Предусмотреть вывод на экран в виде таблицы значений аргумента X и вычисленных значений Y.
Вариант 9 1.Вычислить и вывести на экран значение функции
2. Произвести вычисление значения функции Z. Предусмотреть вывод на экран значения X и вычисленных значений Y и Z.
3.Табулирование функции на интервале с заданным шагом. Предусмотреть вывод на экран в виде таблицы значений аргумента k и вычисленных значений Y.
Вариант 10 1.Вычислить и вывести на экран значение функции
2. Произвести вычисление значения функции Z. Предусмотреть вывод на экран значения X и вычисленных значений Y и Z.
3.Табулирование функции на интервале с заданным шагом. Предусмотреть вывод на экран в виде таблицы значений аргумента X и вычисленных значений Y.
Вариант 11 1.Вычислить и вывести на экран значение функции
2. Произвести вычисление значения функции Z. Предусмотреть вывод на экран значения X и вычисленных значений Y и Z.
3.Табулирование функции на интервале с заданным шагом. Предусмотреть вывод на экран в виде таблицы значений аргумента X и вычисленных значений Y.
Вариант 12 1.Вычислить и вывести на экран значение функции
2. Произвести вычисление значения функции Z. Предусмотреть вывод на экран значения X и вычисленных значений Y и Z.
3.Табулирование функции на интервале с заданным шагом. Предусмотреть вывод на экран в виде таблицы значений аргумента k и вычисленных значений Y.
Вариант 13
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.1.63 (0.008 с.) |

 :
: 
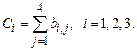
 , j = 1, 2, 3, 4.
, j = 1, 2, 3, 4.