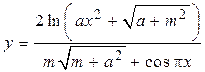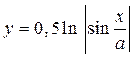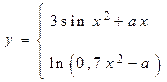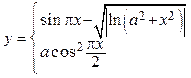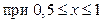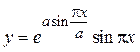Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка одномерных массивовСодержание книги
Поиск на нашем сайте
Как было указано выше, в Вasic-программе массив должен быть описан с помощью оператора DIM(N), в результате работы которого резервируется память в объеме N ячеек. Для обработки элементов массива необходимо задать числовые значения всем его элементам. Это может быть сделано в результате ввода числовых значений последовательно в каждую ячейку памяти оператором INPUT или оператором READ из блока DATA. Кроме того, элементы данных могут вычисляться в соответствие с алгоритмом или генерироваться датчиком случайных чисел с помощью процедуры RND. После заполнения числовой информацией области памяти элементы массива обрабатываются в соответствие с алгоритмом. Пусть описан массив Х(10). Обработка массива, как правило, осуществляется с помощью операторов цикла, значение управляющей переменной служит указателем текущего номера элемента. Когда указатель принимает i-е значение, рассматривается элемент массива с номером i и значением Х(i). Пример: N Вычислить значение функции: G = max { Хi }+ ∏ Хi Xi > 2 i=1
10 INPUT N 20 DIM X(N) 30 P=1 40 FOR I=1 TO N 50 INPUT X(I): NEXT I 60 FOR I=1 TO N 70 IF X(I)>2 THEN P=P*X(I) 75 NEXT I 80 MAX=X(1) 90 FOR I=1 TO N 100 IF X(I)> MAX THEN MAX=X(I) 110 NEXT I 120 PRINT “ X “ 130 FOR I=1 TO N 140 PRINT X(I); 150 NEXT I 160 PRINT 170 PRINT “ G= “; MAX+P 180 END
В строках 40-50 описан цикл ввода элементов массива по запросу с дисплея. В строках 60-75 программы - цикл накопления произведения элементов массива, удовлетворяющих условию Хi> 2. Начальное значение произведения Р=1. В строках 80-110 реализуется поиск максимального элемента среди элементов массива Х. В операторе 80 в качестве претендента на максимальное значение фиксируется 1-й элемент массива. Строка 120 - печать заголовка массива. Операторы в строках 130 - 150 реализуют вывод в строку элементов массива Х. Оператор PRINT без параметров в строке 160 обеспечивает пропуск строки и установку курсора на первую позицию следующей строки. В строке 170 выводится значение искомого выражения под именем G. Использование вложенных циклов при работе с индексированной Переменной Циклический процесс может иметь так называемые вложенные циклы, когда циклический фрагмент программы может содержать другой циклический фрагмент. В таком случае первый из них называют внешним, второй – внутренним. При организации таких процессов необходимо следить, чтобы циклы не пересекались, цикл, открытый первым, должен быть закрыт последним.
Чаще всего вложенные циклы используются при работе с матрицами - таблицами, состоящими из М строк и N столбцов. Необходимо учесть, что при организации вложенных циклов чаще изменяется значение управляющей переменной во внутреннем цикле. Например, для просмотра элементов строк матрицы необходимо фиксировать строку во внешнем цикле и просматривать элементы столбцов внутри этой строки во внутреннем цикле. И, наоборот, для просмотра элементов столбцов необходимо фиксировать во внешнем цикле столбец и во внутреннем цикле перебирать элементы строк в этом столбце. Например: вычислить элементы квадратная матрицы A(N,N) размерности N по формулe А(I,J)=(I-1)*(3)j-2 и значение выражения N G = 1 + ∑ Xi, i=1 где компоненты вектора Х - средние арифметические значения элементов столбцов матрицы А. 10 INPUT N 20 DIM A(N,N), X(N) 25 PRINT " исходная матрица A " 30 FOR I=1 TO N 40 FOR J=1 TO N 50 A(I,J)=(I-2)*3^(J-1) 55 PRINT A(I,J); 60 NEXT J 70 PRINT 80 NEXT I 90 FOR J=1 TO N 100 X(J)=0 110 FOR i=1 TO N 120 X(J)=X(J)+A(I,J) 130 NEXT I 140 X(J)=X(J)/N: S=S+X(J): NEXT J 150 PRINT “вектор X - средние арифметические элементы столбцов “ 160 FOR I=1 TO N 170 PRINT X(I):; NEXT I: PRINT: PRINT “ значение функции G= “; 1+S
В операторах 25-55 под заголовком “исходная матрица A” выводятся вычисленные в этом цикле элементы матрицы А в виде квадратной таблицы, состоящей из N строк и N столбцов. Вектор Х должен быть образован из средних арифметических значений элементов столбцов, поэтому имеет смысл внешний цикл организовать по столбцам, внутренний – по строкам выбранного столбца. При J=1 фиксируется 1-й столбец и вычисляется сумма элементов строк в этом столбце Х(1)=А(1,1)+А(2,1)+… +А(N,1) и т.д. для I=2, N После окончания работы внешнего цикла эта сумма усредняется, и, таким образом, в компоненте X(1) оказывается среднее арифметическое элементов 1-го столбца, в Х(2) – 2-го и т.д. Переменная с именем S, начальное значение S которой равно 0, используется для вычисления суммы элементов массива Х. В операторах 150-160 выводятся на экран компоненты вектора X в строку под заголовком “вектор Х - средние арифметические элементы столбцов”.
Оператором PRINT “ значение функции G= “; 1+S выводится значение выражения.
ЗАДАНИЯ ДЛЯ ЛАБОРАТОРНЫХ И САМОСТОЯТЕЛЬНЫХ РАБОТ Задание 1. Составить блок-схему алгоритма и программу вычисления функций:
Задание 2. Составить блок-схему алгоритма и программу разветвляющегося процесса: 1. 3.
5.
7.
9.
11. 13.
15.
17.
19. Задание 3. Табулирование функции на интервале Составить блок-схему алгоритма с известным числом повторений в цикле и написать программу, вычисляющую значения функции в заданном диапазоне значений х c шагом
Задание 4. Программирование алгоритмов циклической структуры
Составить блок-схему алгоритма и программу циклической структуры: 1. Вычислить факториал произвольного натурального числа N. 2. Найти числа Фибоначчи, не превышающие 50 (числа Фибоначчи - это члены последовательности, в которой каждый последующий элемент равен сумме двух предыдущих (например: 1,1,2,3,5,8,13,21...)). 3. Найти числа Фибоначчи, не превышающие 20. 4. Найти числа Фибоначчи, не превышающие 30. 5. Найти числа Фибоначчи, не превышающие 40. 6. Найти число размещений без повторений А и число повторений С по формулам: А =n!/(n-r)! C =n!/r! × (n-r)! 7. Напечатать все Пифагоровы числа, не превышающие 20. Тройка натуральных чисел, удовлетворяющих равенству a2+b2=c2, называются Пифагоровыми числами. Например: 32 + 42 = 52. 8. Напечатать все Пифагоровы числа, не превышающие 30. 9. Напечатать все Пифагоровы числа, не превышающие 40. 10. Напечатать делители числа N принадлежащие интервалу (2,7). 11. Найти количество делителей числа М, кратных 3. 12. Найти сумму четных делителей числа В. 13. Найти произведение нечетных делителей числа К, принадлежащих интервалу (3,9). 14. Используя алгоритм Евклида, найти наибольший общий делитель (НОД) двух натуральных чисел М и N. Алгоритм Евклида: пусть M и N - одновременно не равные нулю целые неотрицательные числа, тогда: а) если M равно N, то наибольший общий делитель найден и он равен M; б) если M и N не равны (например, пусть M > N, найдите разницу между этими числами и ее значение присвойте большему; в данном случае M=M-N); в) перейти на п. а) алгоритма Евклида. 15. Найти наименьшее общее кратное чисел N и M. (Используя алгоритм Евклида, см. задание 14). 16. Проверить, являются ли числа А и B взаимно простыми. (Числа, у которых наибольший общий делитель равен единице, называются взаимно простыми). 17. Напечатать все простые числа, не превышающие 29. 18. Проверить, является ли заданное число K совершенным. (Совершенным числом называется число, равное сумме всех своих делителей, меньших, чем оно само. Например: 28=1+2+4+7+14). 19. Найти сумму четных делителей числа К, превосходящих 5. 20. Найти произведение нечетных делителей числа К, превосходящих 5. 21. Найти значение выражения С= n!/r! – (n+r)2 при заданных целых n,r.
22. Найти значение выражения С= (n+1)!/r! – (n-r)2 при заданных целых n,r, n>r. 23. Найти значение выражения С= (n-2)!/r! + (n-r)! при заданных целых n,r, n>r. 24. Найти сумму нечетных делителей числа К, превосходящих 5. 25. Найти сумму четных делителей числа К из интервала (3,7). 26. Напечатать все простые числа, не превышающие 17. 27. Напечатать все простые числа, не превышающие 25. Задание 5. Составление алгоритмов и программ обработки Одномерных массивов
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.139.131 (0.008 с.) |


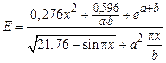





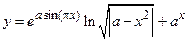
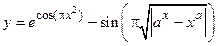













 2.
2. 
 4.
4. 
 6.
6. 
 8.
8. 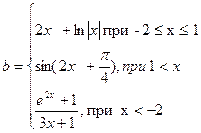
 10.
10. 
 12.
12. 
 14.
14. 
 16.
16. 
 18.
18. 
 20.
20. 
 Значения параметров a, b, m, n, k, q задать произвольно.
Значения параметров a, b, m, n, k, q задать произвольно.