
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центры тяжести простейших тел (тонких однородных пластин и линий)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Т а б л и ц а 5.2. Центры тяжести простейших однородных объемных тел
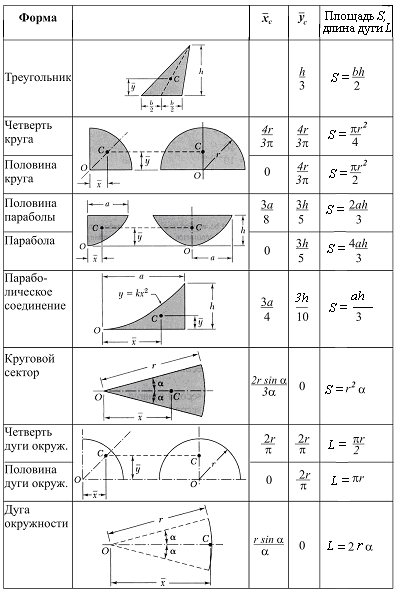
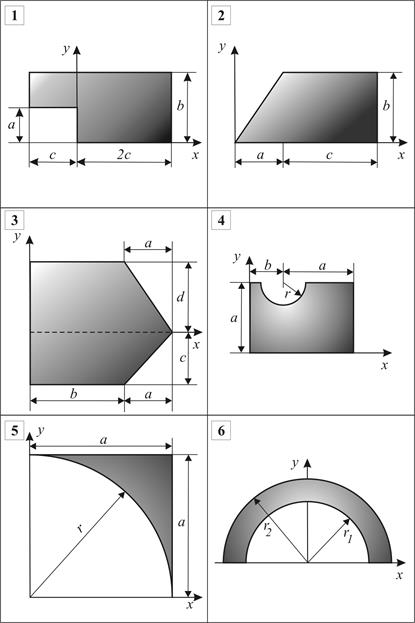
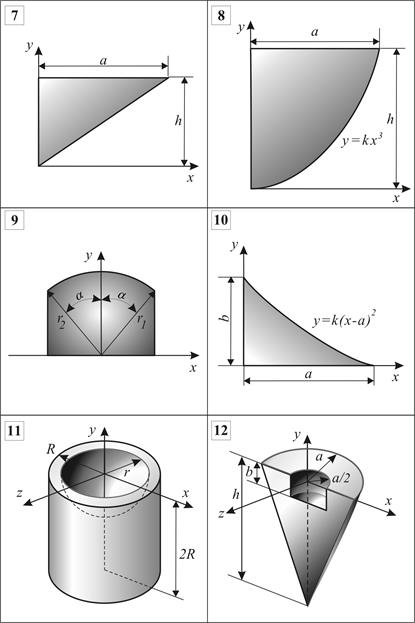
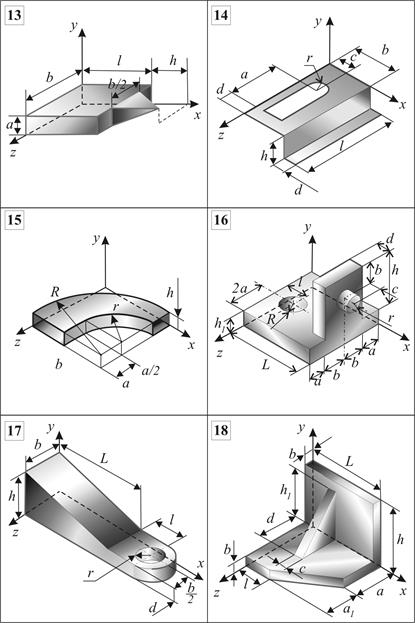
РАСЧЕТНАЯ РАБОТА №5. Центр тяжести однородных плоских фигур и линий Определить центры тяжести однородных плоских фигур, линий и объемных тел, схемы которых представлены на рис.5.12, за исключением варианта 21, где приведена схема неоднородного объемного тела (скамейка). Исходные данные (размеры – в метрах) приведены ¾ в табл. 5.3.При выполнении данной расчетной работы рекомендуется пользоваться таблицами для определения центра тяжести простейших тел в зависимости от их геометрической формы ¾ для тонких однородных пластин и линий (стержней) - табл.5.1 и ¾ для однородных объемных тел -табл.5.2, а также примерами расчета, приведенными в разделе.5.2. Для вариантов 11-21 задача сформулирована конкретно в соответствии с номером варианта на рис.5.12.
Рис. 5.12. Схемы плоских фигур к расчетной работе №5
Рис. 5.12 (продолжение)
Рис. 5.12 (продолжение)
Рис. 5.12 (окончание) Исходные данные к расчетной работе № 5
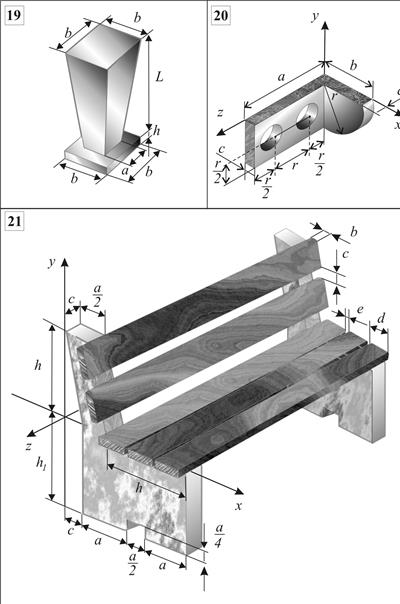
Вариант 11. Определить а) координату Вариант 12. Определить координату Вариант 13. Определить а) координату Варианты 14, 15, 20. Определить координаты центра тяжести тел при заданных их размерах. Вариант 16, 17, 18. Определить координаты Вариант 19. Садовый постамент состоит из пирамиды, установленной на плите высотой Вариант 21. Определить координаты и размерами каждой доски: толщина - b, ширина - d, длина L =1.18 м. Пример 5.7 выполнения расчетной работы № 5. Определение положения центра тяжести половины сплошного кругового конуса, представленного на рис.5.13.
Рис. 5.13 Так как плоскость xy -плоскость симметрии, то центр тяжести лежит в этой плоскости, а координата
Координаты центра тяжести
где Из рис. 5.13 видно, что Объем половины сплошного кругового конуса находим как
Момент выделенного дифференциального элемента относительно плоскости yz есть
Таким образом, абсцисса центра тяжести тела определяется по формуле
Аналогично находим полный моментрассматриваемоготелаотносительно плоскости xz
Ордината центра тяжести тела
КОМПЬЮТЕРНЫЕ ВАРИАНТЫ ЗАДАЧ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 659; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.102.18 (0.006 с.) |


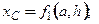
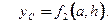
 Определить прямым
интегрированием координаты центра тяжести
пластины как функции
Определить прямым
интегрированием координаты центра тяжести
пластины как функции 
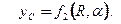
 как функции
как функции 


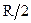
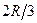
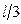
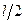
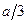
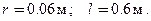

 м, L =0.1 м.
м, L =0.1 м.
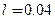 м, L =0.12 м.
м, L =0.12 м.
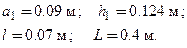
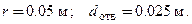
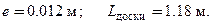

 центра тяжести полого цилиндра с радиусами
центра тяжести полого цилиндра с радиусами 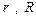 и высотой
и высотой 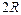 , т.е.
, т.е.  для дискретных значений
для дискретных значений  , приведенных в табл. 5.7 и b) ¾ соотношения
, приведенных в табл. 5.7 и b) ¾ соотношения  для дискретных значений
для дискретных значений 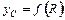 .
.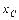 центра тяжести тела для дискретных значений
центра тяжести тела для дискретных значений 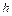 , приведенных в табл. 5.3, т.е.
, приведенных в табл. 5.3, т.е. 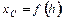 и b) ¾ соотношения
и b) ¾ соотношения 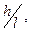 для дискретных значения
для дискретных значения  , т.е.
, т.е.  .
.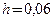 м. Определить а) центр тяжести постамента от его верхней плоскости, b) ¾ минимальную высоту плиты
м. Определить а) центр тяжести постамента от его верхней плоскости, b) ¾ минимальную высоту плиты 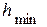 , при которой центр тяжести постамента не будет превышать 0.3 м от его верхней плоскости.
, при которой центр тяжести постамента не будет превышать 0.3 м от его верхней плоскости.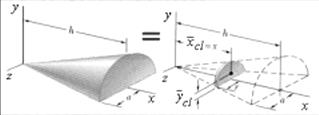
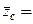 0. Толщина выделенного элемента dx, объем которого определяется как
0. Толщина выделенного элемента dx, объем которого определяется как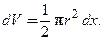
 и
и 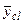 выделенного элемента определяются как
выделенного элемента определяются как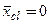 ,
,  ,
,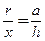 , откуда находим
, откуда находим 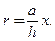

 ; Полный моментрассматриваемоготелаотносительно этой же плоскости
; Полный моментрассматриваемоготелаотносительно этой же плоскости

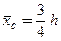 ◄
◄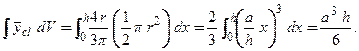
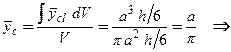
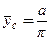 ◄
◄


