
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равновесие связанных (сочлененных) телСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Системой сочлененных твердых тел называют несколько твердых тел, соединенных между собой посредством шарниров, стержней, нитей или касающихся друг друга. Во многих случаях требуется найти силу, с которой одно сочлененное тело действует на другое. Такая задача обычно решается путем рассмотрения каждого тела системы в отдельности. При рассмотрении отдельного тела остальные тела системы будут являться связями, наложенными на это тело, и заменяются реакциями связями. При этом необходимо помнить, что силы взаимодействия двух тел для системы являются внутренними, они равны между собой по абсолютной величине, имеют общую линию действия и направлены в разные стороны. Поэтому при рассмотрении равновесия системы всех тел, вместе взятых, внутренние силы не должны входить в уравнения равновесия. Систему уравнений можно получить, записав уравнения равновесия для системы в целом и для одной части системы в отдельности. Когда же нужно определить силы во внутренних связях, применяют метод, связанный с расчленением системы на части. Для каждой части имеем три независимых условия равновесия (всего их шесть), из совместного решения которых можем найти шесть неизвестных. РАСЧЕТНАЯ РАБОТА №3 Равновесие сочлененных тел
Схемы конструкций плоских систем сочлененных тел представлены на рис.3.5, линейные размеры и действующие на конструкцию нагрузки - в табл. 3.3. Определить силывзаимодействия, возникающие в промежуточном шарнире B, и усилия вподдерживающихсоставную конструкцию опорах, пренебрегая весами балок.
Рис. 3.5. Схемы конструкций сочлененных тел к расчетной работе № 3
Рис. 3.5 (продолжение)
Рис. 3.5 (окончание) Т а б л и ц а 3.3 Исходные данные к расчетной работе № 3
Пример 3.3 выполнения расчетной работы № 3. Р авновесие плоской произвольной системы сил, приложенной к системе связанных (сочлененных) между собой тел; в данном случае соединенных идеальным шарниром С. Схема составной конструкции показана на рис.3.6,а. Дано: на составную конструкцию (система двух тел: балка АС и балка СВD) действуют: сосредоточенная сила Определить: реакции в жесткой заделке А, момент в заделке Решение. При рассмотрении равновесия составной конструкции в целом (АСВD) к системе приложены активные силы Поставленную задачу можно записать коротко следующим образом: ACBD Число неизвестных (
Рис. 3.6 Расчетная схема из двух составных частей показана на рис.3.6,б. Каждая из частей находится в равновесии под действием произвольной плоской системы сил. Для каждой части конструкции можно составить по три уравнения равновесия, приняв ту же систему координат x y (x –по горизонтали вправо, y – по вертикали вверх). Рассмотрим равновесие правой части (CBD) системы: CBD К правой части системы CBD приложены неизвестные 1. 2. 3. Рассмотрим равновесие левой части (AC) системы: AC К левой части AC балки приложены неизвестные силы 4. 5. 6. Из (1): Из (3): Из (2): Из (4): Из (5): Из (6): Для проверки полученных результатов можно составить уравнение моментов относительно какой-либо точки или уравнение проекций на ось x или y как для всей конструкции, так и для отдельных частей. Любое из этих уравнений при равновесии и подстановке полученных значений реакций должно рав няться нулю.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 800; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.92.64 (0.01 с.) |








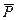 , момент пары сил М и равномерно распределенная по закону прямоугольника нагрузка интенсивности q на участке ВС, P =2 кН; М = 7 кН·м; q =5 кН/м; a =3м; b =2м; d =4м; α = 30˚. В точке А балка АС жестко заделана в стене, а балка СВD опирается на катковую опору (подвижный шарнир) B. Заменимравномерно распределенную по закону прямоугольника нагрузку сосредоточенной силой
, момент пары сил М и равномерно распределенная по закону прямоугольника нагрузка интенсивности q на участке ВС, P =2 кН; М = 7 кН·м; q =5 кН/м; a =3м; b =2м; d =4м; α = 30˚. В точке А балка АС жестко заделана в стене, а балка СВD опирается на катковую опору (подвижный шарнир) B. Заменимравномерно распределенную по закону прямоугольника нагрузку сосредоточенной силой  =
=  . приложенной посередине участка ВС.
. приложенной посередине участка ВС. , реакцию в подвижном шарнире B и давление в промежуточном шарнире С.
, реакцию в подвижном шарнире B и давление в промежуточном шарнире С.
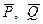 и активная пара сил с моментом
и активная пара сил с моментом  Кроме того, на балку наложены связи: жесткая заделка А, катковая опора B. Отбрасывая мысленно связи, заменяем их действие реакциями (рис.3.6,а). Реакция жесткой заделки (табл.2.1, вар.13) заменяется неизвестной силой
Кроме того, на балку наложены связи: жесткая заделка А, катковая опора B. Отбрасывая мысленно связи, заменяем их действие реакциями (рис.3.6,а). Реакция жесткой заделки (табл.2.1, вар.13) заменяется неизвестной силой  с двумя составляющими
с двумя составляющими 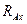 ,
,  , и моментом заделки
, и моментом заделки 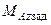 ; реакция опоры B заменяетсянеизвестной силой (табл. 2.1, вар.4)
; реакция опоры B заменяетсянеизвестной силой (табл. 2.1, вар.4)  . Оси координат выберем с началом в точке А, направив абсциссу по горизонтали вправо, ось ординат по вертикали вверх. В результате получаем следующую силовую схему конструкции (рис.3.6,а).
. Оси координат выберем с началом в точке А, направив абсциссу по горизонтали вправо, ось ординат по вертикали вверх. В результате получаем следующую силовую схему конструкции (рис.3.6,а).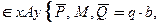
 ,
, 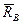
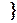 .
. ) – четыре, то есть больше числа уравнений равновесия - три, которые можно составить для этой системы сил. Поэтому для решения данной задачи составную конструкцию необходимо разделить на две части (т.е. на две подсистемы АС и СВD) по промежуточному шарниру С (рис.3.6,б). В месте разделения конструкции необходимо показать соответствующие реакции по взаимно противоположным направлениям для каждой из частей. Причем, соответствующие составляющие реакций равны по величине.
) – четыре, то есть больше числа уравнений равновесия - три, которые можно составить для этой системы сил. Поэтому для решения данной задачи составную конструкцию необходимо разделить на две части (т.е. на две подсистемы АС и СВD) по промежуточному шарниру С (рис.3.6,б). В месте разделения конструкции необходимо показать соответствующие реакции по взаимно противоположным направлениям для каждой из частей. Причем, соответствующие составляющие реакций равны по величине.

 ,
, 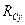 ,
,  P×cos a×+
P×cos a×+ 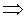
 P×sin a- Q -
P×sin a- Q - 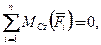 P×sin a
P×sin a  - Q × b/2 +
- Q × b/2 +  = 0.
= 0. 
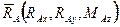 ,
, 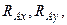
 . Силы в точке C равны по величине и противоположны по направлению силам
. Силы в точке C равны по величине и противоположны по направлению силам 


