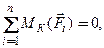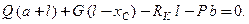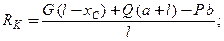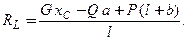Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равновесие тела, которое может опрокидыватьсяСодержание книги
Поиск на нашем сайте
При выполнении расчетной работы №1 на опрокидывание рассматривается предельное положение, когда тело находится в состоянии неустойчивого равновесия и может перейти из состояния покоя в движение. Всякое даже незначительное изменение элементов конструкции или сил, действующих на тело, ведет к опрокидыванию (вращению) конструкции вокруг некоторой оси, называемой осью опрокидывания. Некоторые активные силы, приложенные к телу, образуют пары, которые стремятся опрокинуть тело. Сумма моментов таких сил относительно оси опрокидывания называется моментом опрокидывания; другая часть активных сил создает пары, которые стремятся возвратить тело в исходное положение. Сумма моментов этих сил относительно оси опрокидывания называется моментом устойчивости. Определить: * вес противовеса Схемы конструкций механических кранов представлены на рис.3.1, а исходные данные: веса Элементы конструкции принимаются абсолютно жесткими, стержневые детали - сплошными и невесомыми, трение в шарнирах и опорах отсутствует.
Пример 3.1 выполнения расчетной работы №1. Р авновесие плоской произвольной системы сил, приложенной к одному телу, которое может опрокидываться. Дано: Механический кран (рис.3.2) веса
Рис. 3.1. Схемы конструкций механических кранов к расчетной работе № 1
Рис. 3.1 (продолжение)
Рис. 3.1 (окончание) Исходные данные к расчетной работе №1
Продолжение табл. 3.1
Окончание табл. 3.1
расстояниеотносительно опоры K, на котором должен располагаться противовес для обеспечения максимальной грузоподъемности крана, равно Решение. Рассмотрим равновесие крана (рис.3.2). К нему приложены активные заданные силы: вес крана Теперь рассматриваем равновесие крана как свободного тела, находящегося под действием сил Опрокидывание ненагруженного крана под действием противовеса возможно вокруг левой опоры K в направлении против часовой стрелки, при этом кран правой опорой L только касается поверхности, не оказывая на нее никакого давления. Поэтому вес противовеса находится из условия равенства моментов опрокидывания и устойчивости
Максимально загруженный кран может опрокидываться вокруг правой опоры L по часовой стрелке. Поэтому уравнение моментов составим относительно точки L.
Из полученного уравнения находим наибольший вес поднимаемого груза
Для определения реакций в опорах крана составим уравнения равновесия для полученной системы сил по третьей форме ¾ два уравнения моментов относительно опор K и L:
Из полученных уравнений находим искомые реакции
РАСЧЕТНАЯ РАБОТА №2
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.195.127 (0.007 с.) |

 , при котором не произойдет опрокидывание ненагруженного крана; * максимальный вес
, при котором не произойдет опрокидывание ненагруженного крана; * максимальный вес  груза, который сможет поднять кран; * реакции в опорах крана
груза, который сможет поднять кран; * реакции в опорах крана  при максимальной нагрузке.
при максимальной нагрузке. кранов, положение центра тяжести C и линейные размеры - в табл 3.1.
кранов, положение центра тяжести C и линейные размеры - в табл 3.1. установлен на горизонтальной поверхности. Расстояние между опорами
установлен на горизонтальной поверхности. Расстояние между опорами  , абсцисса центра тяжести крана
, абсцисса центра тяжести крана  , вылет стрелы крана относительно опоры
, вылет стрелы крана относительно опоры 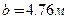 ,
,
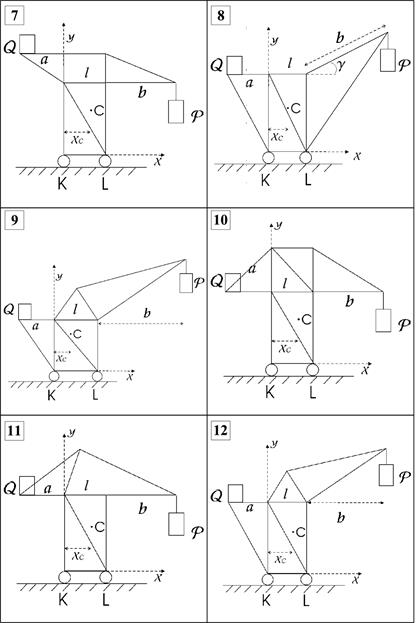


 .
.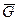 , вес груза
, вес груза 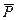 и вес противовеса
и вес противовеса 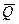 . На кран наложены
. На кран наложены  две связи - катковые опоры K, L, которые не допускают смещения крана вниз от опорной поверхности по вертикали, но не препятствуют его повороту вокруг точек K, L. Так как трением в опорах пренебрегаем, то реакции опор будут направлены нормально к поверхности.
две связи - катковые опоры K, L, которые не допускают смещения крана вниз от опорной поверхности по вертикали, но не препятствуют его повороту вокруг точек K, L. Так как трением в опорах пренебрегаем, то реакции опор будут направлены нормально к поверхности. ,
,  .
.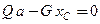 , откуда
, откуда  =
=  .
.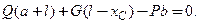
 =27 кН.
=27 кН.