
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равновесие плоской произвольно расположенной системы силСодержание книги
Поиск на нашем сайте Определить реакции связей. Схемы конструкций представлены на рис.3.3, исходные данные – в табл.3.2, где G - сила тяжести, P - активная сила,
Рис. 3.3. Схемы конструкций к расчетной работе № 2
Рис. 3.3 (продолжение)
Рис. 3.3 (окончание) Т а б л и ц а 3.2 Исходные данные к расчетной работе № 2
Окончание табл. 3.2
Пример 3.2 выполн е ния расчетной работы № 2. Р авновесие плоской произвольно расположенной системы сил. Схема балки показана на рис.3.4.
углы α =60°; ß =30˚. Определить: реакции опор Решение. Рассмотрим равновесие балки АВ под действием заданных активных сил. Для составления уравнений равновесия необходимо равномерно распределенную по закону прямоугольника нагрузку на заданном участке балки b заменить равнодействующей, равной численно площади заштрихованной фигуры-прямоугольника Q=q·b= 2·3=6 кН, и приложенной в центре тяжести этой фигуры. Освобождаем систему от связей, направив реакцию Поставленную задачу можно записать коротко следующим образом: AB Так как число неизвестных реакций ( Составим уравнения равновесия плоской системы сил, приложенной к балке АВ: 1. 2. 3. Из (3):
Из (1): Bp (2): Для проверки полученных значений опорных реакций можно составить дополнительное уравнение равновесия:
Ответ:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 626; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 - равномерно распределенные нагрузки, M - момент.
- равномерно распределенные нагрузки, M - момент.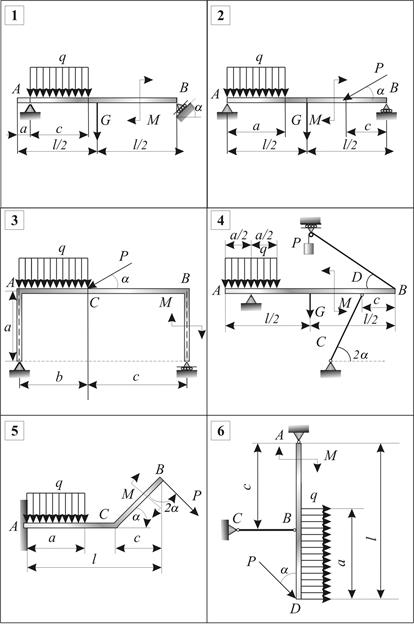


 Дано: Горизонтальная балка АВ нагружена системой сил: сосредоточенной силой Р = 4 кН, моментом М = 5 кН×м пары сил и равномерно распределенной нагрузкой интенсивности q = 2 кН/ м; размеры а = 2м; b =Зм; d =2 м;
Дано: Горизонтальная балка АВ нагружена системой сил: сосредоточенной силой Р = 4 кН, моментом М = 5 кН×м пары сил и равномерно распределенной нагрузкой интенсивности q = 2 кН/ м; размеры а = 2м; b =Зм; d =2 м; и
и  , пренебрегая весом балки АВ.
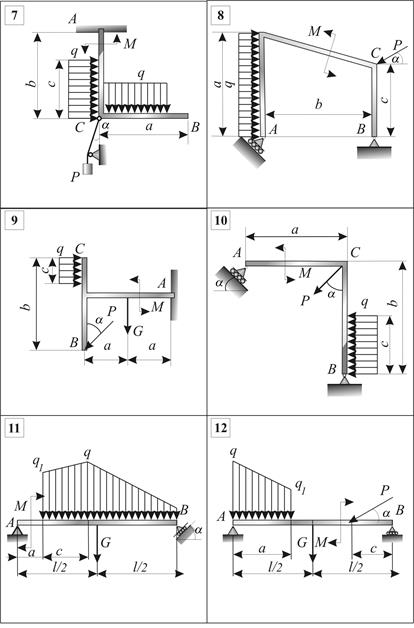
, пренебрегая весом балки АВ.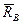 в катковой опоре (подвижном шарнире В) перпендикулярно плоскости опоры, а реакцию внеподвижном шарнире А заменяем двумя составляющими -
в катковой опоре (подвижном шарнире В) перпендикулярно плоскости опоры, а реакцию внеподвижном шарнире А заменяем двумя составляющими -  .
.
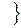 .
.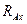 ,
, 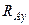 ,
,  ) равно трем, то рассматриваемая задача является статически определимой.
) равно трем, то рассматриваемая задача является статически определимой.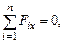 P×cos a-
P×cos a- 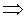
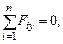 - P×sin a- Q +
- P×sin a- Q +  +
+  -P× a× sin a - Q ×
-P× a× sin a - Q × 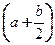 - M +
- M +  × cos b = 0.
× cos b = 0.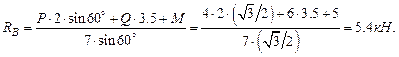
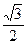 + 6 - 5.4
+ 6 - 5.4  -
-  0=0, значит, реакции определены верно.
0=0, значит, реакции определены верно.


