Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отношения между простыми суждениями.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Логический квадрат Для иллюстрации отношений между простыми суждениями различных типов используется логический квадрат. Он и в самом деле представляет собой геометрический квадрат с проведенными в нем диагоналями, в углах которого мы ставим буквы A, E, I, O, обозначающие типы суждений. Между этими суждениями с одними и теми же субъектом и предикатом возможны следующие отношения: противоречия, или контрадикторности; противоположности (противности), или контрарности; подпротивности, или субконтрарности; подчинения. Все эти отношения наглядно представлены логическим квадратом (рис. 2.2).
Схема 2. Логический квадрат
Самым простым является отношение подчинения, существующее между общими и частными суждениями: А – I, Е – О. Общие суждения называются подчиняющими, а частные – подчиненными. Если общее суждение истинно, то подчиненное суждение также истинно, но не наоборот. Когда частное суждение ложно, то соответствующее общее суждение будет обязательно ложным, но не наоборот. Между суждениями типа А – Е имеет место отношение противоположности (противности): эти суждения не могут быть одновременно истинными, но могут быть одновременно ложными. Проверьте это положение по логическому квадрату на примерах: «Все металлы есть элементы» – истинно, «Все бизнесмены корыстолюбивы» – ложно. Отношение между суждениями типа I – O называют отношением подпротивности: суждения этого типа могут быть одновременно истинными («Некоторые люди искренни»), однако они не могут быть одновременно ложными («Некоторые люди не имеют сердца»). В отношении противоречия находятся суждения А и О, E и I, расположенные на диагоналях логического квадрата. Для этого отношения характерно то, что противоречащие друг другу суждения не могут быть одновременно истинными, но не могут быть и одновременно ложными. Если ложно суждение «Все люди злы», то истинным будет «Некоторые люди не злы».
Модальные суждения Еще одно деление простых суждений на виды – по модальности (от лат.modus – образ, способ). Модальность – это дополнительная информация о характере зависимости между реальными явлениями, о логическом статусе суждений, об оценочных, регулятивных и других характеристиках. Приведем примеры модальных суждений: «Ни один человек не может жить без пищи», «Каждый гражданин обязан соблюдать законы», «Возможно, что существуют внеземные цивилизации», «Иногда неудовлетворительные оценки (как, впрочем, и отличные) студенты получают на экзаменах случайно», «Замечательно, когда люди приветствуют друг друга при встрече», «Неизвестно, знал ли он о моих подозрениях».
Наиболее важными и распространенными выступают четыре вида модальности: · алетическая, или истинная, модальность (от греч. aleteja – истина) выражает характер связи между мыслимыми предметами, а, следовательно, между субъектом и предикатом суждения. Модальные слова – «возможно», «необходимо», «случайно» и их синонимы. С точки зрения алетической модальности различают суждения: а) ассерторические (суждения о факте, действительности чего-либо); б) проблематические (суждения о возможности чего-либо); в) аподиктические (суждения о необходимости чего-либо); · деонтическая, или нормативная, модальность (от греч. deon – нужное, должное) относится к деятельности людей, нормам их поведения в обществе. Модальные слова – «разрешается», «запрещается», «обязательно» и их аналоги. С точки зрения деонтической модальности различают: а) суждения о наличии (отсутствии) какого-либо права; б) суждения о наличии (отсутствии) какой-либо обязанности; · эпистемическая, или познавательная, модальность (от греч. episteme – знание) означает характер и степень достоверности знания. Модальные слова – «доказуемо», «недоказуемо», «опровержимо» и им подобные. С точки зрения эпистемической модальности различают суждения, основанные на вере, и суждения, основанные на знании; · аксиологическая, или ценностная, модальность (от греч. axios – ценный) выражает отношение человека к ценностям – материальным и духовным. Модальные слова – «хорошо», «плохо», «безразлично» (в ценностном отношении) и др. Все формы проявления модальности суждений исследуются модальной логикой, это обширная, относительно самостоятельная и быстро развивающаяся отрасль современной логики.
Сложное суждение Сложным называется суждение, содержащее логические связки и состоящее из нескольких простых суждений. Простые суждения обозначаются отдельными латинскими буквами: a, b, c, d,… Отвлекаясь от сложной внутренней структуры простого суждения, его количества и качества, мы удерживаем лишь одно свойство суждения – то, что оно может быть истинным или ложным. Логические связки представляют собой формальные аналоги союзов нашего родного естественного языка. Как сложные предложения строятся из простых с помощью союзов «однако», «или» и т. п., так и сложные суждения строятся из простых с помощью логических связок.
Вопрос об истинности или ложности простых суждений в конечном итоге всегда решается посредством обращения к той реальности, к которой относятся наши суждения. Но как установить истинность или ложность высказываний с логическими связками, т. е. сложных суждений? Поскольку это не вопрос конкретных наук и материальной практики, а чисто логический, в логике приняты договоренности относительно того, когда высказывания с той или иной логической связкой считаются истинными, а когда – ложными. Соглашения такого рода выражаются таблицами истинности. Для характеристики истинностных значений сложных суждений необходимо знать определения основных логических операций, посредством которых образуются сложные суждения иp простых и способы табличного определения их истинности. · Конъюнкция двух или нескольких простых суждений образуется путем их объединения логической связкой «и» (в естественном языке ей соответствуют союзы «и», «а», «но», «однако», «да», «хотя» и т. п.). Чаще всего конъюнкция обозначается символом «&». Пример: «Никто не забыт, и ничто не забыто», схема – a & b. Такое сложное суждение называют соединительным. Условия истинности суждения a & b могут быть продемонстрированы таблицей истинности. Для построения такой таблицы в левых столбцах важно соблюдать порядок чередования значений «истина» и «ложь» для конъюнктов. Для этой цели у суждения b значения «истина» и «ложь» чередуются друг за другом, а у суждения a два раза используется значение «истина», два раза – «ложь».
Суждение a & b истинно только в том случае, если истинны входящие в него конъюнкты; во всех других случаях конъюнктивное суждение ложно.
Вообще, количество строк в таблице задано количеством переменных. Они вычисляются по формуле: 2n, где n – количество переменных. Если переменных 2 (как в примере), то строк будет 4; если 3 – 8; если 4 – 16 т.п. Приведем пример построения таблицы истинности для трех переменных (a, b, c).
Обратите внимание, что чередование значений «истина»-«ложь» у переменной aдано через 4, у переменной b – через 2. Таким способом строится таблица не только для соединительных, но и для любых других сложных суждений. · Дизъюнкция двух или нескольких простых суждений образуется путем объединения их логической связкой «или» («либо»). Оператор дизъюнкции обозначается символом «V». Пример: «У данногобольного растяжение связок или ушиб», схема – а V b. Сложное суждение такого типа называют разделительным. Рассмотрим истинность дизъюнкции, для чего вновь обратимся к таблице истинности:
Суждение а V b истинно во всех случаях, кроме того, когда два его члена (дизъюнкта) ложны.
· Строгая (исключающая) дизъюнкция объединяет простые суждения исключающей связкой «или – или» («либо – либо») и обозначается символом «
Истинность строгой дизъюнкции выглядит следующим образом (см. ниже расположенную таблицу):
· Импликация состоит в образовании сложного суждения из двух простых посредством логической связки, обозначаемой словами «если…, то», приблизительно соответствующей условному предложению в естественном языке, и выглядит следующим образом: a → b. Пример: «Если через проводник проходит электрический ток, то проводник нагревается».Первый член импликации называется основанием (антецедентом), второй – следствием (консеквентом). Такое суждение называют условным. Составим таблицу истинности для импликативного суждения (см. ниже следующую таблицу):
Импликация ложна только в том случае, если из истинности антецедента вытекает ложность консеквента. В других случаях импликативное суждение истинно.
· Эквивалентность (равнозначность) объединяет два суждения с взаимной (прямой и обратной) условной зависимостью. Она называется еще двойной импликацией, образуется посредством логической связки «если и только если», «тогда и только тогда, когда», обозначается так: a ↔ b или a ≡ b. «Если и только если человек достиг пенсионного возраста, то он имеет право на получение пенсии по возрасту».
Если оба простых суждения принимают одинаковые значения, то эквивалентное суждение истинно, в других случаях – ложно. · Отрицание, с помощью которого из данного суждения образуется противоречащее ему высказывание. Языковая форма – «не», «неверно, что», символическая – «
При отрицании истинное значение суждения сменяется на ложное, и наоборот.
Мы рассматривали до сих пор лишь самые элементарные сложные суждения, состоящие из двух простых суждений и одной логической связки. Однако логические связки могут соединять и сложные суждения, порождая, таким образом, все более сложные структуры. Например, суждение «Мы получим большое удовольствие, если пораньше освободимся и сходим в сауну» в записи выглядит так: (b&c)→a. Сводная таблица истинности сложных суждений строится по следующему принципу: какими бы ни были суждения a или b, если они принимают значения, выписанные в двух левых столбцах приведенной ниже таблицы, то суждения, образованные связыванием их отрицанием, конъюнкцией, дизъюнкцией (простой и строгой), импликацией, эквиваленцией, принимают значения, выписанные в шести правых столбцах.
Нетрудно заметить, что определение истинности сложного суждения сводится, в сущности, к вычислению ее на основе значений истинности простых суждений. При некотором навыке процесс вычисления с помощью таблицы можно ускорить. Сокращенный способ вычисления истинности сложного суждения основывается на установлении главной логической операции в рассматриваемой формуле. Вопросы для самопроверки 1. Чем отличается логическая структура суждения от грамматической структуры предложения? 2. Приведите пример распространенного повествовательного предложения и выделите в нем логический субъект, предикат и логическую связку. 3. Чем отличается нормативная логика от классической логики? В чем состоит специфика нормативных и оценочных суждений? Какую структуру имеют нормы? 4. Какая связь существует между алетической и деонтической модальностями? Перечислите известные Вам виды модальностей. 5. Почему конъюнкцию опровергнуть легче, чем дизъюнкцию?
Задачи и упражнения
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 1008; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.72.189 (0.01 с.) |


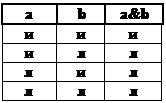

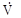 » или «V». К примеру, формальный вид суждения «Пациент либо жив, либо мертв» таков: a
» или «V». К примеру, формальный вид суждения «Пациент либо жив, либо мертв» таков: a 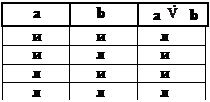 Поскольку a и b исключают друг друга, постольку они не могут быть ни одновременно истинными, ни одновременно ложными.
Поскольку a и b исключают друг друга, постольку они не могут быть ни одновременно истинными, ни одновременно ложными.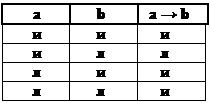
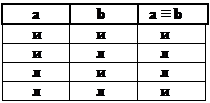
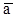 » или «
» или «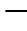 а». Например, «Неверно, что Земля шар», схема –
а». Например, «Неверно, что Земля шар», схема –