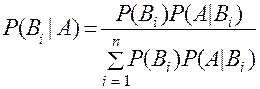Імовірність події і її обчислення.

 

У природній мові існує багато виразів, близьких по значенню слову вірогідність: це і “правдоподібність”, і “ступінь упевненості”, і “ступінь підтвердження”. Аналогічно прикметник “вірогідний” може означати все, що не є повністю визначеним, а може служити для позначення найсприятливішої альтернативи.

Інтуїтивне розуміння того, таке вірогідність події властиво будь-якій людині із здоровим глуздом. Людина оточена безліччю випадкових подій і явищ, які він підсвідомо (або свідомо) оцінює по вірогідності, розрізняючи серед них вірогідні, маловірогідні або неправдоподібні події. Наприклад, подія, яка полягає у тому, що футбольна команда вищої ліги Динамо (Київ) програє колективу фізичної культури можна вважати подією з малою вірогідністю.

Теорія вірогідності зародилася з потреб теорії ігор. У середині століття французькі математики Б.Паскаль і П.Фермі розробили математичну модель, що описує вірогідність результатів в іграх, залежної від випадку. Першим визначенням вірогідності можна рахувати те, яке Б. Паскаль дав в листі до П. Фермі 28 жовтня 1654 року “ступінь можливості (упевненості) події я назвав вірогідністю”.

Існують різні методи визначення вірогідності як чисельної міри ступеня об'єктивної можливості події.

Лабораторна робота 7

«Розрахунок ймовірностей випадкових подій в спорті»

1. Означення умовної імовірності.

2. Формула повної імовірності.

3. Формула Байєса

4. Контрольні питання до лабораторної роботи

Література:

1. Ашанин В.С. Основы теории вероятностей. Серия «Спортивная информатика», вып.4 - Харьков.: ХаГИФК, 1998. –179 с.,

2. Лапач С.Н., Чубенко А.В., Бабич П.Н. Статистические методы в медико-биологических исследованиях с использованием Excel. – 2-е изд. перераб. и доп. – К.: МОРИОН, 2001. – 408 с..

3. Начинская С.В. Основы спортивной статистики. - К.: Вища школа, 1987. – 189 с

4. Толбатов Ю.А. Загальна теорія статистики засобами EXCEL. Навчальний посібник. – К.: Четверта хвиля, 1999.-224 с

Хід лабораторної роботи:

Теоретичний матеріал

Означення умовної імовірності.

Вірогідність події А, обчислена при умові що мала місце інша подія В, називається умовною вірогідністю події А і позначається Р (А | У).

Якщо подія А не залежить від події В, то Р (А | У) = Р (А).

Іншими словами, подія А не залежить від події В, якщо вірогідність події А не залежить від того, відбулося чи ні подія В.

Умовна вірогідність події А рівна відношенню вірогідності подій А і В до вірогідності події В:

Р (А | У) = Р (А Ç В) / Р (В)

Формула повної імовірності.

 

За допомогою умовної вірогідності записується широко вживана в теорії вірогідності формула про повну вірогідність і формула Байеса.

Хай подія А може наступити тільки за умови появи однієї з подій В1, В2..., Вn, створюючих повну групу несумісних подій, тоді вірогідність події А рівна сумі творів вірогідності кожної з подій В1, В2..., Вn на відповідну умовну вірогідність події А:

Дане співвідношення називають формулою повної вірогідності.

 

Формула Байєса:

 

Приклад. Два стрільці незалежно один від одного стріляють по одній мішені, роблячи кожен по одному пострілу. Вірогідність попадання в мішень для першого стрільця 0,8, для другого 0,4. Після стрілянини в мішені знайдена одна пробоїна. Знайти вірогідність того, що ця пробоїна належить першому стрільцю.

До досвіду можливі наступні події (гіпотези):

В1 - ні перший, ні другий стрілець не потрапить;

В2 - обидва стрільці потраплять;

В3 - перший стрілець потрапить, а другої немає;

В4 - перший стрілець промахнеться, а другий потрапить.

 

Вірогідність цих подій:

Р (В1) = 0,2 × 0,6 = 0,12; Р (В2) = 0,8 × 0,4 = 0,32;

Р (В3) = 0,8 × 0,6 = 0,48; Р (В4) = 0,2 × 0,4 = 0,08.

Умовна вірогідність спостереження події А при цих гіпотезах рівні:

Р (А | В1) = 0; Р (А | В2) = 0; Р (А | В3) = 1; Р (А | В4) = 1.

Після досвіду гіпотези В1 і В2 стають неможливими, а вірогідність гіпотез В3 і В4 буде рівна:

Отже, вірогідність того, що пробоїна належить першому стрільцю, рівна 6 / 7.

Практична частина