
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон повного струму в інтегральній форміСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Розглянемо магнітостатичне поле нескінченно тонкого провідника зі струмом
Для розв'язку прямої задачі магнітостатики необхідно оцінити роботу сил магнітостатичного поля по переміщенню пробного заряду уздовж замкненої траєкторії
і називається циркуляцією вектора Випадок 1: контур
оскільки геометрична сума векторів
Згідно з рис.2.4
звідки:
Це означає, що циркуляція вектора
Випадок 2: контур
в якій перший інтеграл є робота поля по переміщенню пробного магнітного заряду по траєкторії
Отже, якщо контур Об'єднуючи результати розгляду обох випадків, сформулюємо закон повного струму в інтег-ральній формі: цирку-ляція вектора
На основі цього зако- ну можна розв’язувати пряму задачу магнітостатики – за відомими значеннями електричних струмів знайти напруженість створеного ними магнітостатичного поля. Однак існує ще й обернена задача – за відомими параметрами магнітостатичного поля необхідно знайти в просторі розподіл електричних струмів, які є джерелами цього поля. За допомогою (2.9) не можна відповісти на питання про наявність струму усередині контуру, оскільки алгебраїчна сума струмів може дорівнювати нулю і при їх наявності, якщо існуючий сумарний струм одного знаку усередині контуру дорівнює сумарному струму іншого знаку. Але ж при розв'язуванні оберненої задачі необхідно знайти значення струму в кожній точці простору. Тому необхідно перейти до нескінченно малої частини області простору, тобто до закону повного струму в диференційній формі.
|
||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 746; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.163.134 (0.009 с.) |

 , напрямленим “від нас” (рис.2.4). При цьому крива, яка в кожній точці має дотичну, що співпадає з вектором
, напрямленим “від нас” (рис.2.4). При цьому крива, яка в кожній точці має дотичну, що співпадає з вектором  за напрямком, є силовою лінією напруженості магнітного поля. На рис. 2.4 позначимо її пунктиром. В даному випадку сімейство силових ліній магнітостатичного поля є концентричні кола, а їх напрям визначається правилом правого гвинта з поступальним рухом в напряму струму
за напрямком, є силовою лінією напруженості магнітного поля. На рис. 2.4 позначимо її пунктиром. В даному випадку сімейство силових ліній магнітостатичного поля є концентричні кола, а їх напрям визначається правилом правого гвинта з поступальним рухом в напряму струму 
 . Ця робота визначається у загальному випадку інтегралом по замкненому контуру
. Ця робота визначається у загальному випадку інтегралом по замкненому контуру 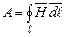
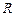 відстань від провідника до елемента контуру
відстань від провідника до елемента контуру 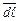 , через
, через  і
і  – проекції відрізку
– проекції відрізку  на напрям
на напрям 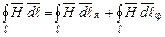 , (2.7)
, (2.7) , (2.8)
, (2.8) . При цьому на основі виразів (2.6), (2.7) і (2.8) одержуємо:
. При цьому на основі виразів (2.6), (2.7) і (2.8) одержуємо: ,
, .
. провідників із струмами
провідників із струмами  , то відповідно з принципу суперпозиції циркуляція сумарного магнітного поля
, то відповідно з принципу суперпозиції циркуляція сумарного магнітного поля  ,
, і
і  . Тоді циркуляцію вектора
. Тоді циркуляцію вектора 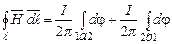 ,
, .
.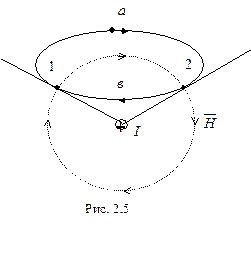
 чисельно дорівнює алгебраїчній сумі стру-мів, охоплених цим контуром, тобто визнача-ється виразом
чисельно дорівнює алгебраїчній сумі стру-мів, охоплених цим контуром, тобто визнача-ється виразом . (2.9)
. (2.9)


