
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнітне поле постійного струму. Закон біо–савара
Протікання в провіднику постійного електричного струму приводить до з'явлення навколо нього магнітного поля. Основним його параметром є вектор напруженості
На відміну від електричного заряду ізольований магнітний заряд одного знаку в природі не існує. Скільки б не зменшували розміри на-магніченого тіла, у нього завжди будуть існувати два полюси. Але для побудови теорії магнітостатики за аналогією з електростатикою доцільно отримати магнітний заряд одного знака хоч би формально. Це можна зробити, якщо магнітний стрижень (рис. 2.1) помістити в металеві ошурки, то останні будуть стягнуті до полюсів тим сильніше, чим більше довжина стрижня Напруженість магнітостатичного поля
Визначення характеристик магнітостатичного поля за заданим значенням і розподілу в просторі постійного струму визначає сутність прямої задачі магнітостатики. В основі розв'язування цієї задачі лежить закон Біо–Савара, відкритий експериментальним шляхом.
Розглянемо нескінченно тонкий провідник довжиною
де
Закон Біо–Савара свідчить про те, що напруженість магнітостатичного поля, яке збуджується елементом постійного струму, прямо пропорційна величині цього елементу, обернено пропорційна квадрату відстані до точки нагляду і залежить від напряму до неї. При цьому добуток
звідки напруженість магнітного поля:
Враховуючи введені позначення, Отже, переходячи від інтегрування по довжині
Виражаючи відстань
і підставляючи її в вираз (2.5), одержимо:
Співвідношення (2.6) свідчить про те, що лінія вектора Застосування закону Біо–Савара для аналізу поля провідника кінцевої товщини або усередині його супроводжується складнощами інтегрування по об'єму, оскільки цей закон справедливий лише для нескінченно тонких провідників. Тому є необхідність в розробці на основі закону Біо–Савара способу розрахунку магнітного поля “товстого” провідника з постійним струмом. Такий спосіб засновується на законі повного струму, який розглянемо нижче. Інтегральну форму цього закону застосовують для розв'язку прямої задачі магнітостатики.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 501; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.132.194 (0.008 с.) |
 , яка відповідно до закону Кулона для магнітних зарядів, визначається співвідношенням:
, яка відповідно до закону Кулона для магнітних зарядів, визначається співвідношенням: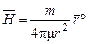 , (2.1)
, (2.1)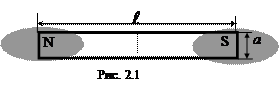 де
де 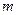 – магнітний заряд;
– магнітний заряд;  – абсолютна магнітна проникність середовища;
– абсолютна магнітна проникність середовища; 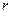 – відстань до точки нагляду;
– відстань до точки нагляду;  – одиничний вектор.
– одиничний вектор. і менше його товщина
і менше його товщина 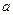 . Припустимо, що
. Припустимо, що 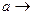 0,
0, 
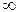 . При цьому взаємодія полюсів
. При цьому взаємодія полюсів  і
і  стане зникаюче малою, тобто магнітні заряди будуть формально розділеними. Одержана таким чином нескінченно тонка і нескінченно довга магнітна “спиця” названа фіктивною магнітною масою, а рознесені на нескінчену відстань полюсу магніту при цьому формально являють відокремлені магнітні заряди протилежних знаків, а значення будь-якого з них входить у співвідношення (2.1).
стане зникаюче малою, тобто магнітні заряди будуть формально розділеними. Одержана таким чином нескінченно тонка і нескінченно довга магнітна “спиця” названа фіктивною магнітною масою, а рознесені на нескінчену відстань полюсу магніту при цьому формально являють відокремлені магнітні заряди протилежних знаків, а значення будь-якого з них входить у співвідношення (2.1). . Для усунення цієї залежності введемо нову характеристику магнітостатичного поля – вектор магнітної індукції:
. Для усунення цієї залежності введемо нову характеристику магнітостатичного поля – вектор магнітної індукції: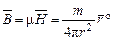 . (2.2)
. (2.2)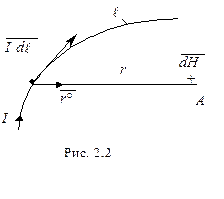
 з постійним струмом
з постійним струмом 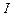 (рис.2.2). Виділимо елемент довжини провідника
(рис.2.2). Виділимо елемент довжини провідника  , при цьому добуток
, при цьому добуток  розглядається як вектор і називається елементом струму. Він збуджує в точці нагляду
розглядається як вектор і називається елементом струму. Він збуджує в точці нагляду 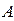 елементарне магнітостатичне поле напруженості
елементарне магнітостатичне поле напруженості 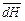 , яке визначається за законом Біо–Савара векторним добутком:
, яке визначається за законом Біо–Савара векторним добутком: , (2.3)
, (2.3) ;
; 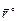 визначає модуль і напрям елементу
визначає модуль і напрям елементу 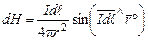 ,
,
 . (2.4)
. (2.4)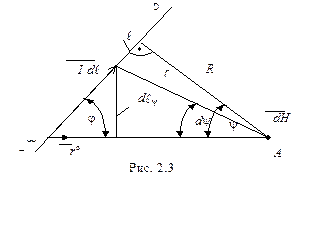 Розглянемо приклад практичного застосування закону Біо–Савара для визначення напруженості постійного магнітного поля, яке створюється прямолінійним нескінченно довгим і нескінченно тонким провідником з електричним струмом
Розглянемо приклад практичного застосування закону Біо–Савара для визначення напруженості постійного магнітного поля, яке створюється прямолінійним нескінченно довгим і нескінченно тонким провідником з електричним струмом  . Позначимо:
. Позначимо: 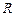 - найкоротша відстань від точки нагляду
- найкоротша відстань від точки нагляду  – відстань від точки A до елемента струму
– відстань від точки A до елемента струму 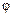 – кут, який характеризує напрямок на точку
– кут, який характеризує напрямок на точку  – кут між нормаллю до провідника і напрямом на точку
– кут між нормаллю до провідника і напрямом на точку 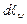 – проекція
– проекція  на нормаль до
на нормаль до 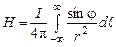 ,
,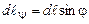 . Внаслідок нескінченної малості
. Внаслідок нескінченної малості 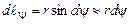 .
.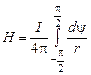 . (2.5)
. (2.5)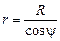
 . (2.6)
. (2.6)


