
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Гауса–ОстроградськогоСодержание книги
Поиск на нашем сайте
Для об’єднання інтегральної (1.4.) та диференційної (1.8) форм рівності Гауса–Остроградського використаємо зв’язок сумарного заряду
то сумарний заряд знаходиться інтегруванням
Тоді рівність (1.4) можна переписати у вигляді:
але відповідно з виразом (1.8)
Одержане співвідношення (1.11), яке є аналогом (1.4), відоме під назвою теореми Гауса–Остроградського. Співвідношення зв’язує поверхневий інтеграл з об’ємним, дозволяючи оперативно міняти порядок інтегрування. Це суттєво спрощує рішення ряду задач, коли замість обчислення складних інтегралів можна змінити порядок одного з них, а потім прирівняти підінтегральні функції інтегралів, що зв’язані знаком рівності.
1.6. Робота сил та потенціал електричного поля
Нехай в електростатичному полі точкового заряду Сила, яка діє на заряд
Робота сили
Повна робота сил поля при переміщенні заряду
З одержаного співвід-ношення випливає, що робота сил електричного поля не залежить від форми шляху, а визначається найкоротшою відстанню між початковою і кінцевою точками. Цей висновок зроблений для поля точкового заряду електростатичного поля. Розглянемо роботу сил електростатичного поля по переміщенню пробного заряду
Такий інтеграл називається циркуляцією вектора
На ділянці
оскільки відстань між початковою та кінцевою точками в обох випадках одна і та ж сама. Таким чином, робота сил по замкненому контуру, або циркуляція вектору
Цей результат очевидний тому, що він випливає із закону збереження енергії. Оскільки робота по переміщенню заряду є лише функцією відстані між початковою та кінцевою точками, то стає можливим введення скалярного параметру поля – його потенціалу. Різність потенціалів між двома точками дорівнює взятій з протилежним знаком роботі сил електростатичного поля при перенесенні одиниці кількості електрики з однієї точки в іншу:
Уявимо тепер, що точка
де За одиницю потенціалу (в системі одиниць СІ) прийнятий один Вольт. Для поля сукупності зарядів потенціал відповідно з принципом суперпозиції дорівнює сумі окремих потенціалів:
Таким чином, електростатичне поле визначається як векторами
|
|||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.214.78 (0.009 с.) |

 в деякому об’ємі
в деякому об’ємі 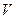 з об’ємною густиною зарядів. Якщо густина зарядів – це відношення заряду до одиниці об’єму
з об’ємною густиною зарядів. Якщо густина зарядів – це відношення заряду до одиниці об’єму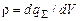 ,
, за об’ємом
за об’ємом  :
: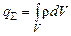 .
. ,
,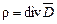 . При цьому
. При цьому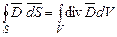 (1.11)
(1.11)
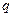 по деякій траєкторії
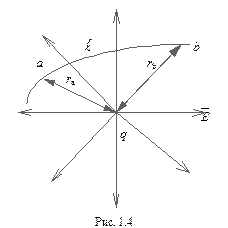
по деякій траєкторії 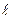 переміщується пробний заряд
переміщується пробний заряд  (рис. 1.4). Розглянемо, яка робота виконується полем при переміщенні цього заряду.
(рис. 1.4). Розглянемо, яка робота виконується полем при переміщенні цього заряду.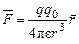 .
. на ділянці шляху
на ділянці шляху  :
:
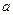 в точку
в точку 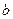 визначається інтегру-ванням
визначається інтегру-ванням 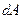 на ділянці
на ділянці  :
: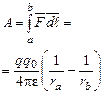 . (1.12)
. (1.12) . В даному випадку робота розраховується інтегруванням
. В даному випадку робота розраховується інтегруванням 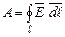 .
.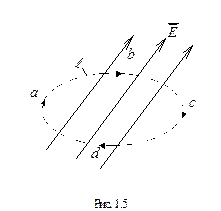
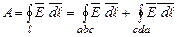 .
.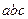 поле витрачає енергію по переміщенню заряду
поле витрачає енергію по переміщенню заряду 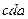 – навпаки, заряд віддає енергію полю. Оскільки робота на ділянці шляху не залежить від форми траєкторії, то можна стверджувати, що
– навпаки, заряд віддає енергію полю. Оскільки робота на ділянці шляху не залежить від форми траєкторії, то можна стверджувати, що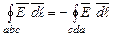 ,
,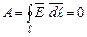 . (1.13)
. (1.13) . (1.14)
. (1.14)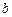 знаходиться на нескінченно великій відстані, тому потенціал в ній дорівнює нулю. Тоді потенціал поля
знаходиться на нескінченно великій відстані, тому потенціал в ній дорівнює нулю. Тоді потенціал поля 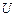 в точці
в точці 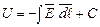 , (1.15)
, (1.15)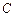 – постійна інтегрування, яка враховує початкові умови.
– постійна інтегрування, яка враховує початкові умови.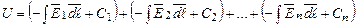 .
. , так і скалярною величиною
, так і скалярною величиною 


