
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон повного струму в диференційній формі
Розглянемо область простору, в якій присутнє магнітостатичне поле Розбиваємо площину Усередині контуру
Інтеграл в лівій частині як математичний оператор має назву циркуляції, а права частина виражає частку сумарного струму, що підлягає дослідженню.
Віднесемо обидві частини цієї рівності до величини
Ліва частина виразу (2.10) є циркуляцією
або:
Розглянемо докладніше диференційний оператор Суцільною лінією зображено проекцію На рис. 2.7 через n позначено нормаль до координатної площини XOY. На неї відмічені проекції Ротор
Таким чином ротор вектору На основі викладеного вище, застосовуючи математичну форму запису оператора “ротор” в прямокутній системі координат, одержимо співвідношення:
яке відображає закон повного струму в диференційній формі: ротор вектора напруженості магнітостатичного поля визначається густиною електричного струму, що створює це поле. В цьому співвідношенні перший доданок є проекцією
Теорема Стокса Між інтегральною і диференціальною формами закону повного струму існує взаємозв'язок, установлений теоремою Стокса. Теорема Стокса зв'язує інтеграли різного порядку, подібно до теореми Гауса–Остроградського в електростатиці. Вона дозволяє оперативно переходити від лінійного інтеграла до поверхневого, і навпаки, що в ряді випадків, наприклад, при розв'язуванні прямої задачі магнітостатики, суттєво полегшує розрахунки. Інтегральна (2.19) і диференціальна (2.12) форми запису закону повного струму такі:
Значення сумарного струму
Підставляючи цей вираз в інтегральну форму закону повного струму, одержуємо:
В правій частини цієї рівності виразимо
тобто циркуляція вектора
Оператор Гамільтона
При розв'язуванні прямої задачі магнітостатики в загальному вигляді кінцевий результат повинен бути представлений у формі функціональної залежності вектора
до якого застосовуються всі правила дії з векторами. Кожна проекція вектора
Розглянемо приклади використання вектора 1. Множення вектора
Якщо скалярній функції
тобто при здійсненні проміжних перетворень операція диференціювання скалярної функції
2. Скалярний добуток векторів На основі правила скалярного множення векторів запишемо:
Порівнюючи співвідношення (2.14) та (1.9) встановимо, що скалярний добуток
Розглянемо скалярний добуток двох векторів
Оператор
співпадає за змістом з операцією типу
Тому рівняння Пуассона–Лапласа, наприклад, може бути представлено у вигляді:
3. Векторний добуток векторів Використовуючи правила векторного добутку двох векторів, одержуємо таке співвідношення:
Це означає, що обчислення ротора будь–якого вектора може бути замінено формально алгебраїчною операцією загального вигляду 4. Обчислення операцій вигляду Записуємо дану функцію через
За визначенням результатом добутку
тоді
Звідси випливає важливий наслідок: якщо дивергенція будь–якого вектора, наприклад,
то
5. Обчислення функцій вигляду Запишемо дану функцію через
За визначенням, градієнт будь–якої скалярної функції
то
Якщо при цьому
6. Обчислення функцій вигляду Запишемо цю функцію через оператор
Всі співвідношення, що отримано, будуть використані у по-дальшому для спрощення математичних дії та при з’ясовуванні фізичного змісту складних явищ.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 935; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.60.166 (0.039 с.) |
 . Необхідно визначити значення струму в певній точці. Для цього замкнений контур
. Необхідно визначити значення струму в певній точці. Для цього замкнений контур  , в якому знаходиться точка, зменшуємо, “стягуючи” його до неї. Площа контуру при цьому буде прямувати до нуля. Якщо виявиться, що в цьому випадку циркуляція
, в якому знаходиться точка, зменшуємо, “стягуючи” його до неї. Площа контуру при цьому буде прямувати до нуля. Якщо виявиться, що в цьому випадку циркуляція  , обмежену контуром
, обмежену контуром  , обмежені контурами
, обмежені контурами 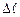 (рис.2.6).
(рис.2.6).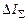 . Тоді відповідно до виразу (2.9):
. Тоді відповідно до виразу (2.9): .
.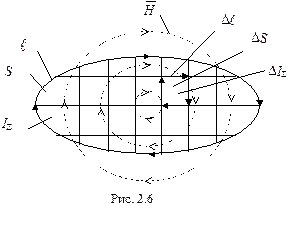
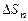 і перейдемо до границі при умові, що
і перейдемо до границі при умові, що  :
: . (2.10)
. (2.10) до елемен-тарної площадки
до елемен-тарної площадки 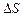 , а права частина – проекцією вектора густини струму провідності
, а права частина – проекцією вектора густини струму провідності 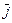 на ту ж нормаль. Тому
на ту ж нормаль. Тому  . Оскільки вектор
. Оскільки вектор 
 . (2.11)
. (2.11)
 . Нехай вектор
. Нехай вектор  контуру
контуру  і
і  , які зв'язані співвідношенням (2.11).
, які зв'язані співвідношенням (2.11).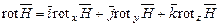 .
.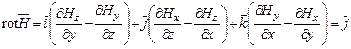 , (2.12)
, (2.12)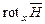 , другий проєкцією –
, другий проєкцією –  , а третій – проєкцією
, а третій – проєкцією  . Таким чином, обернена задача магнітостатики розв’язується шляхом диференціювання по осям координат проекцій відомого вектора напруженості
. Таким чином, обернена задача магнітостатики розв’язується шляхом диференціювання по осям координат проекцій відомого вектора напруженості  ;
;  .
. обчислюється його густиною через інтеграл по поверхні:
обчислюється його густиною через інтеграл по поверхні: .
. .
.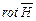 відповідно до закону повного струму в диференціальній формі і одержимо математичний запис теореми Стокса в такому вигляді:
відповідно до закону повного струму в диференціальній формі і одержимо математичний запис теореми Стокса в такому вигляді: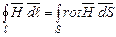 ,
,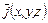 . Для досягнення цієї мети одного співвідношення (2.12) недостатньо, оскільки в ньому містяться три невідомих і підлягаючих визначенню проекції
. Для досягнення цієї мети одного співвідношення (2.12) недостатньо, оскільки в ньому містяться три невідомих і підлягаючих визначенню проекції  вектора
вектора  (набла). Оператор Гамільтона розглядається як формальний вектор
(набла). Оператор Гамільтона розглядається як формальний вектор
 .
. :
: . (2.13)
. (2.13)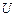 надати зміст потенціалу, то, порівнюючи співвідношення (2.13) та (1.17), приходимо до висновку про те, що
надати зміст потенціалу, то, порівнюючи співвідношення (2.13) та (1.17), приходимо до висновку про те, що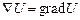 ,
,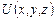 за координатами може бути замінена еквівалентною алгебраїчною операцією
за координатами може бути замінена еквівалентною алгебраїчною операцією  .
.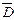 .
.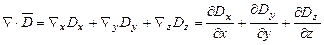 . (2.14)
. (2.14) еквівалентний операції дивергенції над вектором
еквівалентний операції дивергенції над вектором  або будь–яким іншим фізичним вектором, тобто
або будь–яким іншим фізичним вектором, тобто . (2.15)
. (2.15) .
. має зміст операції диференціювання другого порядку і називається оператором Лапласа. Добуток вигляду:
має зміст операції диференціювання другого порядку і називається оператором Лапласа. Добуток вигляду: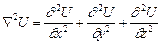
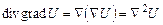 .
. .
. .
.

 . (2.16)
. (2.16) .
.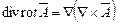 .
. є третій вектор, наприклад,
є третій вектор, наприклад, 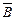 , перпендикулярний площині розташування векторів
, перпендикулярний площині розташування векторів  . Тому вектори
. Тому вектори  ,
, .
. , ротор якого дорівнює початковому вектору
, ротор якого дорівнює початковому вектору 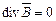 ,
,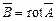 . (2.17)
. (2.17)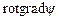 .
. . (2.18)
. (2.18) є вектором, наприклад,
є вектором, наприклад,  . Із співвідношення (2.18) випливає ще один важливий наслідок: якщо ротор будь–якого вектора, наприклад,
. Із співвідношення (2.18) випливає ще один важливий наслідок: якщо ротор будь–якого вектора, наприклад,  , градієнт якої дорівнює початковому вектору. Таким чином, якщо
, градієнт якої дорівнює початковому вектору. Таким чином, якщо ,
,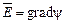 . (2.19)
. (2.19) , де
, де  .
.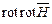 .
.
 . (2.20)
. (2.20)


