
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Граничні умови для тангенційних складовихСодержание книги
Поиск на нашем сайте
вектора
Нехай вектор напруженості магнітного поля
Тут сума другого і четвертого доданків дорівнює нулю, але незалежно від цього розміри сторін
Розміри сторін
де
Тут елементи контуру На основі вище викладеного одержуємо граничні умови для тангенційних складових вектора
або
тобто тангенційні складові вектора 2.7.2. Граничні умови для нормальних складових вектора
Нехай вектор магнітної індукції
Оскільки весь магнітний заряд умовний усередині замкненої поверхні зосереджений на площадці
Враховуючи протилежну напрямленість векторів
Скоротимо скалярні добутки на величину
В одержаному співвідношенні перший член є нормальною складовою
тобто нормальна складова вектора Отже, для вектора
або
тобто нормальні складові вектора У загальному випадку нормальні і тангенційні складові вектора
|
||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.172.190 (0.006 с.) |


 перетинає границю поділу двох середовищ. Елемент вектора
перетинає границю поділу двох середовищ. Елемент вектора 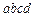 . Від форми контуру циркуляція не залежить, тому вибираємо прямокутний контур, сторони якого нескінченно малі. Напрям обходу контура здійснюємо за годинниковою стрілкою. Циркуляція
. Від форми контуру циркуляція не залежить, тому вибираємо прямокутний контур, сторони якого нескінченно малі. Напрям обходу контура здійснюємо за годинниковою стрілкою. Циркуляція  .
.
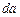 і
і  спрямовуємо до нуля, оскільки необхідно дослідити явища на границі розподілу.
спрямовуємо до нуля, оскільки необхідно дослідити явища на границі розподілу. і
і 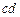 (рис. 2.8) зменшуємо до нескінченно малих значень так, щоб на них можна було вважати H = const. Тоді:
(рис. 2.8) зменшуємо до нескінченно малих значень так, щоб на них можна було вважати H = const. Тоді: ,
,  ,
, і
і  – значення
– значення  .
.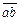 і
і  напрямлені протилежно один до одного (рис.2.8), а
напрямлені протилежно один до одного (рис.2.8), а 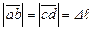 . Тоді добуток
. Тоді добуток 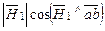 – проекція вектора
– проекція вектора  на границю поділу, тобто вона є тангенційною складовою
на границю поділу, тобто вона є тангенційною складовою 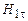 вектора
вектора  . Величина
. Величина  є проекцією вектора
є проекцією вектора  .
. ,
,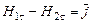 , (2.26)
, (2.26) перетинає границю поділу двох середовищ з різними значеннями
перетинає границю поділу двох середовищ з різними значеннями  і
і  . Виділимо нескінченно малу ділянку поверхні поділу
. Виділимо нескінченно малу ділянку поверхні поділу 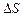 таку, щоб можна було знехтувати її кривизною. Побудуємо циліндр з поперечним перетином
таку, щоб можна було знехтувати її кривизною. Побудуємо циліндр з поперечним перетином  до поверхні поділу. На рис.2.9 застосовані такі позначення:
до поверхні поділу. На рис.2.9 застосовані такі позначення:  і
і  – нижня і верхня основи циліндра;
– нижня і верхня основи циліндра;  – його бокова поверхня. Потік вектора
– його бокова поверхня. Потік вектора 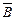 через замкнену поверхню циліндра згідно з виразом (2.21):
через замкнену поверхню циліндра згідно з виразом (2.21):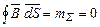 .
. .
.
 і
і  (рис.2.9), можна записати:
(рис.2.9), можна записати: .
. :
: .
. .Тому вираз, який описує граничні умови для нормальних складових вектора магнітної індукції
.Тому вираз, який описує граничні умови для нормальних складових вектора магнітної індукції 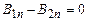 ,
, ,
, , (2.27)
, (2.27) разів.
разів.


