
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики електричного поляСтр 1 из 10Следующая ⇒ Напруженість електричного поля – це сила дії поля на пробний точковий електричний заряд. Позитивним напрямком дії сили прийнято вважати напрямок від позитивного заряду – джерела поля – до точки розташування пробного електричного заряду або в напрямку від більшого заряду до меншого. Визначимо напруженість електростатичного поля
де значення відстані r:
а
де Отже, напруженість поля точкового заряду прямо пропорційна його значенню, обернено пропорційна квадрату відстані до точки спостереження та залежить від напрямку на неї. Вектор
Ця нова характеристика, що не залежить від
Отже, вектор Розглянемо поле точкового заряду
Аналогічно визначають потік вектора
Отже, кількість силових ліній На основі одержаних співвідношень для
1.3. Рівність Гауса – Остроградськогов інтегральній формі
Нехай вектор
Розглянемо замкнену поверхню
Тут Потік вектора
Нехай тепер в об’ємі
де
Тут кожний додаток у відповідності з виразом (1.3) дорівнює
тобто потік вектора
Співвідношення (1.4) є рівністю Гауса–Остроградського в інтегральній формі. Воно свідчить про те, що потік вектора електричної індукції через замкнену поверхню довільної форми дорівнює алгебраїчній сумі зарядів Тепер може виникнути запитання: якщо співвідношення (1.4) дозволяє визначати характеристики поля за відомою кількістю зарядів, то чи не можна скористатися цим же співвідношенням – рівністю Гауса–Остроградського в інтегральній формі - для розв’язування оберненої задачі, тобто знаходження розподілу заряду за відомими характеристиками поля
|
|||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.69.152 (0.005 с.) |
 , створеного точковим зарядом
, створеного точковим зарядом  , що знаходиться у точці з координатами
, що знаходиться у точці з координатами  , в точці спостереження
, в точці спостереження 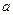 з координатами
з координатами  , в якій знаходиться електричний заряд
, в якій знаходиться електричний заряд 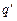 . Відповідно до закону Кулона, на заряд
. Відповідно до закону Кулона, на заряд 
 ,
, – одиничний вектор. Тоді напруженість поля визначимо як силу, що діє на пробний заряд:
– одиничний вектор. Тоді напруженість поля визначимо як силу, що діє на пробний заряд: [В/ м], (1.1)
[В/ м], (1.1) є - радіус-вектор.
є - радіус-вектор. свідчить про залежність
свідчить про залежність  .
. . З урахуванням співвідношення (1.1):
. З урахуванням співвідношення (1.1): .
. з центром у точці розташування заряду. В будь-якій точці такої сфери вектори
з центром у точці розташування заряду. В будь-якій точці такої сфери вектори 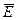 або
або  , що перетинають елемент поверхні сфери, відповідає чисельному значенню
, що перетинають елемент поверхні сфери, відповідає чисельному значенню  .
. .
. напруженість поля E = ¥. Але це суперечить фізичному змісту, тому що ніяка фізична величина не може приймати нескінченних значень. Справа в тому, що поняття “точковий заряд”, тобто заряджене тіло з “нульовими” розмірами, є умовним. Реальне фізичне тіло завжди має кінцеві розміри, які потрібно враховувати при малих відстанях до точки спостереження. Тому в наступному параграфі розглянемо співвідношення для напруженості електричного поля зарядів, розташованих у середині замкненої поверхні.
напруженість поля E = ¥. Але це суперечить фізичному змісту, тому що ніяка фізична величина не може приймати нескінченних значень. Справа в тому, що поняття “точковий заряд”, тобто заряджене тіло з “нульовими” розмірами, є умовним. Реальне фізичне тіло завжди має кінцеві розміри, які потрібно враховувати при малих відстанях до точки спостереження. Тому в наступному параграфі розглянемо співвідношення для напруженості електричного поля зарядів, розташованих у середині замкненої поверхні.
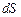 (рис.1.1). Як елемент поверхні
(рис.1.1). Як елемент поверхні  вона є пласкою та характе-ризується визначеною орієн-тацією в просторі. Це означає, що елементарну площадку
вона є пласкою та характе-ризується визначеною орієн-тацією в просторі. Це означає, що елементарну площадку 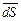 , що спрямований перпендикулярно поверхні
, що спрямований перпендикулярно поверхні  .
. . (1.2)
. (1.2)
 – елементарний ті-лесний кут, під яким площадку
– елементарний ті-лесний кут, під яким площадку 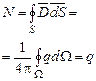 , (1.3)
, (1.3) , обмеженому замкненою поверхнею
, обмеженому замкненою поверхнею  , є безліч зарядів
, є безліч зарядів  . Згідно з принципом суперпозиції для лінійних середовищ результуюче значення вектора:
. Згідно з принципом суперпозиції для лінійних середовищ результуюче значення вектора: ,
, – вектори індукції, які створені зарядами
– вектори індукції, які створені зарядами  в точці спостереження. Тому потік результуючого вектора індукції крізь замкнену поверхню
в точці спостереження. Тому потік результуючого вектора індукції крізь замкнену поверхню  .
. , де
, де  Тоді:
Тоді: ,
, :
: . (1.4)
. (1.4) , які знаходяться в об’ємі, обмеженому цією поверхнею. Ця рівність дозволяє визначити характеристики поля
, які знаходяться в об’ємі, обмеженому цією поверхнею. Ця рівність дозволяє визначити характеристики поля 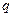 в конкретній точці об’єму, більш того, неможливо навіть відповісти на запитання: чи є взагалі заряди усередині даного об’єму, оскільки алгебраїчна сума зарядів може дорівнювати нулю при однаковій кількості зарядів протилежних знаків.
в конкретній точці об’єму, більш того, неможливо навіть відповісти на запитання: чи є взагалі заряди усередині даного об’єму, оскільки алгебраїчна сума зарядів може дорівнювати нулю при однаковій кількості зарядів протилежних знаків.


