
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рівність Гауса–Остроградського в диференційній формiСодержание книги
Поиск на нашем сайте
Нехай в прямокутній системі координат існує обмежений об’єм Визначимо наявність електричного заряду в деякій точці
Алгебраїчна сума зарядів у се-редині об’єму
де Рис. 1.3. домою величиною потоку N треба зменшувати об’єм стягуючи поверхню
В (1.6) права частина – об’ємна густина зарядів
Згідно з рівнянням (1.6):
Співвідношення (1.8) називається рівністю Гауса–Остроградського в диференційній формі. Визначимо дивергенцію вектора
де Аналогічно потік вектора
де знак мінус показує протилежний напрям зовнішніх нормалей до граней 1 та 2. Загальний потік
де різниця
Тоді:
Аналогічним чином визначаються потоки вектора
При цьому в прямокутній системі координат дивергенція
На основі виразів (1.8) і (1.9) одержимо:
Співвідношення (1.8) та (1.10) дозволяють розв’язувати обернену задачу електростатики – знаходження заряду в конкретній точці, якщо відомі характеристики поля. Однак ці співвідношення неможливо використати для розв’язування прямих задач в загальному вигляді, оскільки в цьому випадку кожне з них містить три невідомих складових вектора Доцільно ввести нову скалярну функцію, яка з одного боку була б зв’язана з питомим зарядом
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.201.19 (0.009 с.) |

 (рис.1.3). Необхідно визначити розподіл в ньому електричних зарядів. Для цього можна було б застосувати рівність (1.4) до нескінченно малого об’єму
(рис.1.3). Необхідно визначити розподіл в ньому електричних зарядів. Для цього можна було б застосувати рівність (1.4) до нескінченно малого об’єму  . Однак тоді отримаємо, що потік вектору
. Однак тоді отримаємо, що потік вектору  через нескінченно малу поверхню є нескінченно малою величиною третього порядку малості. Тому для розв’язування оберненої задачі доцільно розглядати не власно потік, а його відношення до малого об’єму.
через нескінченно малу поверхню є нескінченно малою величиною третього порядку малості. Тому для розв’язування оберненої задачі доцільно розглядати не власно потік, а його відношення до малого об’єму.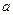 (рис.1.3) усередині об’єму
(рис.1.3) усередині об’єму 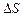 . Потік вектора
. Потік вектора  :
: (1.5)
(1.5)
 ,
, – об’ємна гус-тина зарядів. Для визначення густини заряду в точці a за ві-
– об’ємна гус-тина зарядів. Для визначення густини заряду в точці a за ві- . (1.6)
. (1.6) , а ліва – границя відношення потоку
, а ліва – границя відношення потоку  через замкнену поверхню
через замкнену поверхню  . (1.7)
. (1.7)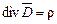 . (1.8)
. (1.8) ,
, – проекція вектору
– проекція вектору  в точці, яка визначає положення грані 1.
в точці, яка визначає положення грані 1. ,
,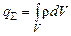 ,
, є прирістом
є прирістом  при зміні
при зміні  і вона дорівнює:
і вона дорівнює: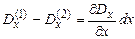 .
. .
. .
. . (1.9)
. (1.9) . (1.10)
. (1.10) . Така функція - потенціал електростатичного поля буде проаналізована далі.
. Така функція - потенціал електростатичного поля буде проаналізована далі.


