
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Граничні умови для потенціалу електричного поля
Вище було показано, що вектор
і відносно пласкої границі уявимо, що:
Тоді:
Виберемо напрямок координатних осей таким чином, щоб вісь
За аналогією з виразом (1.34):
Отже, як видно з наведеного рисунку, на границі розподілу двох
середовищ при
З одержаної рівності на основі граничних умов для тангенційних складових вектора
яке свідчить про те, що потенціал на границі поділу середовищ стрибка не зазнає. Для нормальних складових
Отже, одержані співвідношення (1.31) – (1.36) описують поведінку електростатичного поля при переході з одного середовища в інше. Практичний інтерес представляє частковий випадок, коли одне з середовищ – провідник.
1.9.4. Граничні умови на поверхні ідеального провідника
Як відомо, провідник відрізняється від діелектрика наявністю вільних електронів - негативних зарядів. Ідеальний провідник – це таке середовище, в якому кількість вільних зарядів в одиниці об’єму нескінченно велика. При внесенні ідеального провідника в електростатичне поле в провіднику відбувається перерозподіл зарядів. Негативні заряди накопичуються на тому боці його поверхні, в який входять силові лінії зовнішнього поля, а позитивні заряди індукуються на протилежній. При цьому усередині провідника утворюється електричне поле, в якому силові лінії напрямлені назустріч по відношенню до зовнішнього. Перерозподіл зарядів буде продовжуватись до тих пір, поки внутрішнє поле не компенсує зовнішнє в межах об'єму провідника. Отже, ідеальний провідник – це такий провідник, який має достатню кількість вільних зарядів для компенсації зовнішнього поля в межах всього об'єму провідника. Таким чином, результуюче поле усередині ідеального провідника дорівнює нулю. В загальному вигляді граничні умови для тангенційних складових:
Однак, оскільки усередині ідеального провідника поля немає
Для нормальних складових вектора
але при умові ідеальності провідника другий доданок дорівнює нулю, тому
звідси:
Одержані співвідношення виражають граничні умови на поверхні ідеального провідника: силові лінії електростатичного поля завжди напрямлені по нормалі до поверхні ідеального провідника.
Як ілюстрацію розглянемо електричне поле усередині циліндричного конденсатора. Нехай провідник
де Ємність конденсатора визначимо як модуль відношення заряду до різниці потенціалів між тілами
В загальному випадку електрична ємність провідника – це відношення заряду на його поверхні до потенціалу. Тіло, яке здатне накопичувати заряди, характеризується також енергією, що визначається його електростатичним полем.
|
||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 438; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.190.167 (0.006 с.) |
 зв'язаний з потенціалом поля
зв'язаний з потенціалом поля 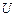 . Розглянемо поведінку потенціалу поля на границі поділу двох середовищ. Згадаємо співвідношення, яке поєднує
. Розглянемо поведінку потенціалу поля на границі поділу двох середовищ. Згадаємо співвідношення, яке поєднує 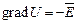 ,
, .
. . (1.34)
. (1.34) лежала в поверхні поділу середовищ, а вісь
лежала в поверхні поділу середовищ, а вісь  співпадала з напрямком нормалі до граничної поверхні (рис. 1.9). Тоді, згідно з граничними умовами (1.31) і (1.33), запишемо:
співпадала з напрямком нормалі до граничної поверхні (рис. 1.9). Тоді, згідно з граничними умовами (1.31) і (1.33), запишемо: .
.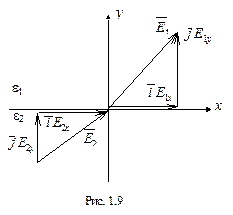
 .
. :
: .
. , (1.35)
, (1.35) (1.36)
(1.36) .
. то
то .
.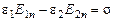 ,
, ,
, .
.
 поміщений в порожнину провідника
поміщений в порожнину провідника  (рис. 1.10). Поле усередині порожнини визначається тільки наявними там електричними зарядами і напрямлене завжди по нормалі до поверхні провідників, причому заряди накопичуються на їх поверхнях. Сумарне значення зарядів відповідно з рівністю Гауса–Остроградського:
(рис. 1.10). Поле усередині порожнини визначається тільки наявними там електричними зарядами і напрямлене завжди по нормалі до поверхні провідників, причому заряди накопичуються на їх поверхнях. Сумарне значення зарядів відповідно з рівністю Гауса–Остроградського: ,
, – площина замкненої поверхні усередині провід-ника
– площина замкненої поверхні усередині провід-ника  ;
;  і
і  – заряди тіл
– заряди тіл  відповідно. Однак, оскільки усередині провідника поля немає, то
відповідно. Однак, оскільки усередині провідника поля немає, то  , звідки
, звідки  . Очевидно, що збільшення заряду
. Очевидно, що збільшення заряду  призведе до росту напруженості і потенціалу електричного поля.
призведе до росту напруженості і потенціалу електричного поля. .
.


