
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Различия в механике поведения окн с металлическим и текстильным кордами. Расчет ндс окн с текстильным кордомСодержание книги
Поиск на нашем сайте
В предыдущих разделах нити корда рассматривались абсолютно жесткими (кроме раздела 3.4, где учитывалась продольная жесткость корда на растяжение). Это не давало возможности сопоставлять расчетные и экспериментальные результаты при условиях перехода нитей корда в ОКН от растяжения к сжатию. Такой режим работы нитей текстильного корда может возникать в каркасе шины при некоторых экстремальных условиях её эксплуатации. Кроме того, нить корда, особенно текстильного, имеет конечную жесткость в поперечном направлении и при продольном сдвиге. В данном разделе излагается метод расчета НДС резинокордных систем на основе текстильного корда с учетом коэффициентов Gkор и Еkор, характеризующихпродольную сдвиговую и поперечную нормальную жесткости корда. Эти свойства корда могут реализоваться в ОКН. Явление сжатия нити корда каркаса шины имеет место при эксплуатации шин с многослойным каркасом, как радиальной, так и диагональной конструкции [[270], [271], [272]]. Определение работоспособности резинокордного слоя в условиях сжатия нити корда представляется весьма актуальной задачей, поскольку изменение геометрических параметров корда в процессе нагружения резинокордного слоя неблагоприятно сказывается на работоспособности изделия [183, [273]]. Таким образом, необходимо иметь возможность описывать процесс деформирования резинокордного композита в условиях сжатия нити корда в продольном направлении. На первом этапе решения следует найти область значений углов наклона нитей корда в ОКН, при которых наблюдается сжатие нити корда. Для этого рассмотрим поведение нити корда в образце. Предположим, что нить корда при продольном сжатии ведет себя аналогично резине, то есть модуль корда на сжатие не отличается от модуля резины на сжатие. Это предположение принято на основании сравнительного анализа эксперимента по растяжению ОКН с j0 = 90° и растяжению образца резины (рис. 3.5.1).
Рис. 3.5.2 Образец ОКН с деформируемыми нитями корда: сверху - до деформации, снизу - в деформированном состоянии.
На основании зависимости степени поперечного сокращения представленных образцов от степени их удлинения (рис. 3.5.1) можно сделать вывод, что отклонение l2 окн от l2 рез достаточно мало (не более 10%). Запишем соотношения, позволяющие рассчитать длину нити корда в деформированном ОКН с учетом принятых выше приближений. Рассмотрим образец ОКН до и после деформирования (рис. 3.5.2). Исходя из однородности резины, её несжимаемости и принятых ранее допущений, имеем:
b0= l0 sinj0 (3.5.1) h0= l0 cosj0 h = h0 lокн Здесь: lокн - степень удлинения образца; j0, j - угол наклона нити к оси растяжения образца до и после деформации; b0, b - ширина образца до и после деформации; l0, l - длина нити до и после деформации.
Длина нити корда в деформированном состоянии может быть определена из соотношения: l2=b2+h2. (3.5.2) Подставив (3.5.1) в (3.5.2), получим соотношение, связывающее относительную длину нити корда с параметрами образца:
Для того, чтобы определить точки максимальной степени сокращения длины нити, требуется продифференцировать соотношение (3.5.3) по lокн и приравнять полученную зависимость к 0. Получим: tg2j0 = 2lокн3. (3.5.4) При подстановке в (3.5.4) значения l=1, получим максимальное значение угла j0, при котором нить корда не сжимается при растяжении образца. Данный угол равен 54,7°. Провели экспериментальное исследование описанного явления сжимаемости нитей корда. Использовали образцы ОКН на основе корда 23 КНТС с углами 45°, 54°, 60°. Полученные результаты обобщены в виде графиков (рис. 3.5.3). Соотношение (3.5.4) получено для случая, когда нити корда имеют модуль, равный модулю резины. Однако для реальных образцов модуль растяжения корда существенно выше модуля растяжения резины. По этой причине, предсказываемое теорией удлинение нитей корда не будет реализовано в эксперименте, и в этой области следует рассматривать длину нитей неизменной при растяжении образца. Предсказанная теорией область сжатия нитей имеет место. Однако, экспериментальная и теоретическая зависимости для j0 =60° различаются существенно (рис. 3.5.3). Данные различия возможны вследствие поперечного деформирования и сдвига нити корда в случае её продольного сжатия (рис. 3.5.4). Для учета этого явления выведем соотношения, описывающие деформацию ОКН с нитями конечной жесткости.
Рис. 3.5.3 Экспериментальные и теоретические зависимости степени сокращения нити корда от степени удлинения образцов.
В качестве исходных используются соотношения (3.5.5), полученные в разделе 3.4, связывающие нормальную деформацию резины между нитями корда ln.рез и тангенциальную деформацию резиновой прослойки gрез в образце типа ОКН с параметрами резинокордного слоя и степенью его удлинения lокн (рис. 3.2.3). Нить корда предполагается абсолютно жесткой.
Здесь (см. рис. 3.2.3): b = d0 / h0 qрез - угол сдвига резины между нитями корда, d0 - начальный диаметр нити корда, h0 - начальное расстояние между центрами соседних нитей, j0, j - угол наклона нити к оси образца до и после деформации.
Если нити корда имеют конечную жесткость в поперечном направлении и в направлении продольного сдвига, то картина деформирования резинокордного слоя, фрагментом которого является образец типа ОКН, имела бы вид, изображенный схематично на рис. 3.5.4 в. Выведем зависимости, аналогичные приведенным выше, для рассматриваемого случая нитей корда конечной жесткости. Запишем некоторые соотношения, которые следуют из рис. 3.5.6
OP= h0 / sin j0 d = d0.ln.кор
Здесь: ln.кор =((ln.рез - 1)×Ekор)+1, gкор = g рез × Gkор h- расстояние между центрами соседних нитей после деформации; q кор -угол сдвига нити корда Из соотношений (3.5.6) легко получить:
Выражения (3.5.7) позволяют более точно, чем (3.5.5), установить связь между деформацией слоя каркаса, определенной экспериментальными методами, и НДС резины между нитями корда. Однако остается открытым вопрос о значениях параметров Еkop и Gkор, прямое определение которых связано со значительными экспериментальными трудностями. Определение Еkop и Gkop может быть осуществлено с использованием соотношений (3.5.5) - (3.5.7). Сравнение с экспериментом проведем для случая, когда при растяжении ОКН нить корда будет находиться в состоянии сжатия. Хорошее совпадение расчетных и экспериментальных зависимостей получено для уравнений (3.5.7) при значениях параметров жесткости Gkор < 1 и Ekор < 1. Это свидетельствует о том, что в состоянии сжатия нить текстильного корда имеет более низкую жесткость в поперечном направлении, чем резина. То же утверждение справедливо и для продольной сдвиговой жесткости корда. Полученные результаты позволяют лучше понять детальный механизм деформирования резинокордных систем с текстильным кордом и могут быть использованы при уточнённом расчете НДС резинокордных слоёв резиновых изделий на основе текстильного корда.
а) б) в)
а- образец до деформации; б- деформированный образец с абсолютно жесткими нитями; в- образец с деформируемыми нитями (нити конечной жесткости);
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 557; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.86.38 (0.006 с.) |

 Рис. 3.5.1 Зависимость степени поперечного сокращения от степени удлинения образцов резины и ОКН с текстильным кордом с углом j=900
Рис. 3.5.1 Зависимость степени поперечного сокращения от степени удлинения образцов резины и ОКН с текстильным кордом с углом j=900

 (3.5.3)
(3.5.3)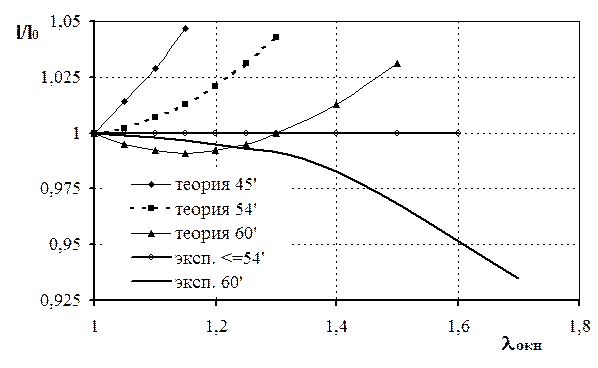
 (3.5.5)
(3.5.5) .
.

 (3.5.6)
(3.5.6) .
.  (3.5.7)
(3.5.7)
 Рис. 3.5.4 Схема деформирования образцов ОКН:
Рис. 3.5.4 Схема деформирования образцов ОКН:




