
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Целевое назначение лабораторных испытаний.
Как мы помним, в работе [14] (раздел 1.4) предложено по своему назначению методы механических испытаний разделить на три группы: общие (физические), специальные, контрольные. Общие или физические методы дают возможность получить показатели, имеющие ясный физический смысл и позволяющие характеризовать некоторые свойства испытуемого материала в строго определенных режимах (однородное НДС, фиксированная скорость, температура, и т.д.). Показатели, получаемые этими методами, могут служить не только для сравнительной оценки, но и в качестве абсолютных характеристик материала. Специальные методы строятся с учетом особенностей режимов переработки материалов или эксплуатации изделия. Авторы [14] считают, что, как правило, эти режимы достаточно сложны и не поддаются строгому анализу. Показатели, получаемые этими методами, следует считать условными и пригодными лишь для сравнительной оценки материалов. Контрольные методы предназначены для испытаний различных партий (образцов) одного и того же материала и служат для обнаружения нежелательных отклонений свойств контролируемого материала от заданных норм. В качестве контрольных методов могут выступать как физические, так и специальные методы. Изложим наше видение данной проблемы. Все виды лабораторных испытаний, предназначенных для прогнозирования работоспособности изделия на стадии проектирования и производства, следует разделить на две группы. Первая – те испытания, на основе которых делается вывод о пригодности данного материала для его использования по назначению. Назовем эти испытания определяющими. Например, для оценки пригодности резинокордной системы для работы в качестве каркаса необходим, в первую очередь, показатель усталостной выносливости (число циклов до разрушения) в тех условиях, в которых работает каркас данной конкретной шины (если требуется, то с учетом многократного восстановления протектора). К условиям работы следует отнести: динамику НДС, температуру, наличие факторов старения. Кроме показателя усталостной выносливости, к определяющим относится величина потерь при качении шины. Этот показатель важен как критерий расхода топлива. Кроме того, он влияет на усталостную выносливость через температуру.
Определяющими являются показатели, связывающие тензоры напряжений и деформаций материалов шины в реальных условиях их нагружения (тензоры модулей упругости в зависимости от температурных и временных условий нагружения). Эти показатели влияют на жесткостные характеристики шины в целом, на шумообразование, комфортность и проч. Безусловно, данные показатели существенно влияют на усталостные свойства и на теплообразование, но в этом смысле они не являются выходными и не используются как определяющие. Обратим внимание, что в число определяющих испытаний не включены методы определения прочности связи на границе «корд-резина». Обоснование этому дано в главе 4. Автомобилисту не важно, какая прочность связи. Ему достаточно, если он будет иметь гарантию, что шина пройдет, допустим, 100 тысяч км. Определяющие испытания включают в себя общие и специальные (по выше данной классификации). Это можно аргументировать самой постановкой задачи. На этапе воспроизведения в лабораторных условиях того, что имеется в изделии, не требуется, например, высокой степени однородности НДС, которая реализуется в современном испытательном оборудовании (UTS, INSTRON, SCHENK, MTS и др.). Вторая группа – контрольные испытания. Здесь мы практически полностью соглашаемся с трактовкой, изложенной в [14]. В эту группу могут входить любые показатели, чувствительные к составу резины, режиму ее вулканизации, условиям старения и испытаний. Перечень показателей, входящих в группу, должен отвечать требованиям оперативности, экономичности и достаточности. Последнее означает, что при обеспечении заданного уровня всех свойств группы гарантируется высокое потребительское качество материала в условиях его технологического использования и эксплуатации. Иными словами, должно быть взаимно однозначное соответствие между измеренными контрольными показателями и потребительским качеством. При этом контролируемые свойства могут не быть непосредственно связанными с эксплуатационными характеристиками изделия. Например, режим растяжения резинового образца-лопатки до разрыва никогда не реализуется в шинах или РТИ, тем не менее, этот показатель всегда используется для контроля качества.
Какой набор контрольных показателей можно считать достаточным? На этот вопрос нет строгого однозначного ответа. Можно лишь пояснить на примере, что имеется в виду при оценке достаточности. Допустим, мы имеем эталонную резину, априори подходящую для данного целевого назначения, например, для работы в качестве обкладки каркаса. Проведем комплекс испытаний для данной резины и определим ее прочность, разрывное удлинение, напряжения при различных степенях удлинения, показатель раздира, величину гистерезиса, остаточное удлинение, адгезионные характеристики и пр.; повторим все это при повышенной температуре и после соответствующих видов старения. Примем в качестве аксиомы следующее утверждение: если для вновь изготовленной резины указанный набор показателей совпадает с набором для эталонной резины, то и определяющие показатели новой и эталонной резин будут совпадать. Правильность этой аксиомы тем очевиднее, чем больше группа контрольных испытаний. Именно этим и пользуются при оценке стабильности качества. Достаточность некоторого набора испытаний для их использования в качестве контрольных определяется эмпирически или методами статистики. В приведенном примере мы говорили только о резине. Безусловно, работоспособность РКК зависит еще и от корда. К нему полностью относится все сказанное. В качестве контрольных испытаний РКК можно дополнительно предложить малоцикловое утомление. Возникает вопрос: зачем проводить большое число контрольных испытаний, если можно провести одно-два определяющих испытания? Ответ прост. Десяток контрольных испытаний во много раз оперативнее и дешевле, чем построение одной зависимости усталостной выносливости от деформации во всем диапазоне действующих нагрузок. Здесь кроется большая опасность. В практике разработки новых резин и РКК часто используют контрольные испытания в качестве определяющих. Этот путь принципиально неверен. Нам неизвестна количественная связь между контрольными и определяющими показателями. Мы можем лишь интуитивно утверждать, что, изменив набор контрольных показателей в лучшую, по нашему мнению, сторону, мы получим улучшение определяющих показателей. Пример: часто гонятся за повышением показателя прочности связи «корд-резина» по Н -методу, а в реальном изделии – шине – эффект не проявляется. Однако создателей резин можно понять. До последнего времени не были разработаны методики для нахождения определяющих показателей, в которых учитывались бы все основные эксплуатационные факторы. Сказанное должно послужить предупреждением об опасности использования неадекватных лабораторных методов испытаний для целей разработки новых материалов. До сих пор в этом разделе мы говорили об уровне свойств, т.е. среднем значении измеряемого показателя. В любой же технической документации качество материалов, в том числе каучуков и резин, определяется, кроме уровня, стабильностью этого уровня. Сам по себе уровень показателей контролируемых свойств не является достаточной характеристикой высокого качества. Не менее, а во многих случаях и более важным является поддержание стабильности этого уровня в течение всего периода производства материала. Не анализируя сейчас причины больших разбросов измеряемых показателей, обратим внимание на то, что единственно надежным способом контроля стабильности является строгая статистическая обработка всех результатов измерений и испытаний. Этой части работ по обеспечению качества уделяется первостепенное внимание не только в стандартах ГОСТ, ISO, ASTM, но и в гораздо большей степени в требованиях крупных зарубежных фирм к качеству поставляемых материалов.
Опустим детальное обсуждение статистических методов обработки результатов испытаний (измерений). Здесь мы не можем сказать что-то новое. В рамках обсуждаемых проблем это не требуется. Все, что нужно, давно и подробно изложено в литературе [274]. Позволим себе лишь небольшое замечание по поводу ГОСТ 269-66 [[279]], где в Приложении описана процедура определения числа испытываемых образцов для получения результата с требуемой точностью при заданной доверительной вероятности. В указанном Приложении сказано, что при определении числа испытываемых образцов следует вначале определять статистические характеристики генеральной функции распределения результатов испытаний. Рекомендуется для этого испытывать не менее 25 образцов и тем больше, чем больше величина коэффициента вариации. Эта рекомендация не достаточная. А сколько же испытывать образцов конкретно? Как убедиться в том, что выборка, по которой определяются моменты генеральной функции распределения, является репрезентативной? Предлагается простая процедура, заключающаяся в следующем. Испытываются 50 образцов. Если первые два момента выборки, содержащей 50 испытаний, отличаются от соответствующих моментов любой из случайных выборок по 25 испытаний (взятых из 50 испытаний) на небольшие, устраивающие нас величины, то можно утверждать, что выборка из 25 испытаний является репрезентативной. Если отличия моментов большие, то следует удвоить число испытаний и опять сравнить между собой результаты по выборкам из 50 и 100 испытаний. Если моменты близки, то выборка из 50 испытаний репрезентативна. Если нет, то процедура повторяется. В таблице 5.2.1 приведены некоторые результаты статистической обработки усталостных испытаний резин на основе разных каучуков. Видно, что разброс показателей существенно больше у резин на основе некристаллизующихся каучуков (БСК, СКД), чем у кристаллизующегося СКИ-3.
Профессиональное применение статистических методов является необходимым условием оценки величины достоверности любого прогноза. Этой тривиальной, но далеко не всегда принимаемой к руководству фразой мы закончим краткое статистическое отступление. Итак, разрабатывать новую резину следует с использованием определяющих методов, а контролировать уровень и стабильность ее качества – с помощью контрольных. Табл. 5.2.1 Статистическая обработка результатов испытаний шинных резин
5.3 Концептуальные вопросы технологического обеспечения качества
Прикладная специфика представленных исследований в области механики резины и РКК заключается в том, чтобы их использовать при разработках новых конструкций шин на стадии проектирования для обеспечения более высокого качества как самого изделия, так и технологического процесса создания этого изделия. Об этом пойдет речь в предлагаемом разделе. Качество продукции является одним из важнейших факторов успешной деятельности любой организации. Под общей системой качества понимается совокупность организационной структуры, ответственности, процедур, процессов и ресурсов, обеспечивающая осуществление общего руководства качеством [[280], [281], [282]]. В этом разделе будут обсуждаться вопросы технологического обеспечения качества шин в условиях автоматизированного компьютеризированного шинного производства. При этом особое внимание будет обращено на методы отбора наиболее значимых показателей из всей совокупности имеющихся, на уточнение системы допусков контролируемых показателей.
Следует отметить, что в условиях автоматизированного производства смещаются акценты при определении методов контроля по сравнению с традиционными методами [[283], [284]]. Предъявляются новые требования к средствам измерения параметров технологического процесса (ТП), к средствам передачи информации в управляющие компьютерные системы, к способам обработки этой информации и алгоритмам выработки оптимальных рекомендаций поддержания ТП в требуемом режиме. Возникает необходимость автоматизированной выработки рекомендаций по корректировке ТП при плановом изменении внешних факторов: использовании нового сырья и материалов, изменении цен, и т. д. Уменьшается степень влияния на качество продукции субъективного фактора. С точки зрения технологии производства качество продукции будет обеспечено, если · все параметры, существенно влияющие на качество продукции, включены в перечень контролируемых параметров, · контролируемые параметры находятся в требуемых пределах. Для такого сложного в технологическом и конструктивном плане изделия, как шина, процесс производства которого начинается с обработки разнородного сырья и материалов (каучук, технический углерод и другие инаполнители, химикаты более чем 20 наименований, корд, бортовая проволока, и др.) и включает в себя множество переделов (смешение материалов с целью изготовления сырой резины, пропитка и обрезинивание корда, заготовка деталей шины, многостадийный процесс сборки шины, формование, вулканизация, и др.), количество контролируемых и регулируемых параметров N измеряется сотнями. Для каждого из них установлены нормы Ai (i = 1, 2 …, N) и допустимые отклонения от норм - допуски DAi. Как правило, значения Ai и DAi: устанавливаются эмпирически. Число показателей М, характеризующих качество готового изделия, существенно меньше, около 10. Сюда входят показатели Вj (j = l,..., M) - масса шины, габариты, жесткостные характеристики, значения максимальной нагрузки на шину и максимальной скорости, сцепные свойства, потери на качение, гарантийный пробег, показатели шума, силовой и геометрической однородности, комфортности и проч. Допуски на эти показатели DBj определяются требованиями заказчика, конъюнктурой рынка и существенно влияют на конкурентоспособность изделия. Очевидно, что не все из N показателей Ai, характеризующих ТП изготовления шин, одинаково существенно влияют на М показателей Bj, характеризующих качество готового изделия. Встает задача выбора из N показателей N*, наиболее важных для получения качественного изделия. Эту задачу можно решить тремя способами [284]. Первый способ - метод экспертных оценок. Он состоит в том, что наиболее квалифицированные специалисты в данной области знаний, основываясь на своем опыте, объявляют некоторые показатели из всех имеющихся наиболее важными, считая при этом, что остальные показатели могут рассматриваться как фоновые, шумовые, влияние которых на качество продукции не превышает некоторого допустимого значения. Второй способ можно назвать «из первых принципов». Здесь используются результаты фундаментальных исследований (теоретических, экспериментальных, компьютерных), позволяющие получать аналитические соотношения между (некоторыми) параметрами ТП, включая свойства сырья, материалов и полуфабрикатов, образующихся в процессе производства, и показателями, характеризующими качество готовой продукции - шины. Из анализа этих соотношений нетрудно определить наиболее значимые параметры. Наконец, третий способ отбора N* наиболее значимых показателей из общего их числа N состоит в применении статистических методов [[285], [286]]. Если для достаточно большого числа однородной продукции (шин одного размера и модели, с использованием одинаковых материалов и технологии изготовления) измерить значения Ai всех N показателей, то известные математические и статистические приемы позволят определить наличие корреляции между конкретными показателями ТП и параметрами качества шин, степень этой корреляции. Кроме этого, статистические методы позволяют прослеживать стабильность работы оборудования, величину разброса измеряемых показателей в зависимости от различных факторов, как объективных (качество сырья, температура и давление пара, степень изношенности оборудования, и др.), так и субъективных (мастерство сборщиков шин, аккуратность наладчиков оборудования, и др.). Переход к автоматизированному шинному производству, кроме очевидных преимуществ в повышении производительности и снижении себестоимости, позволяет в большой степени избавиться от субъективного фактора. Автоматизированное шинное производство легче оборудовать датчиками, измеряющими значения Ai и Bj. Вопрос об установке соответствующих датчиков решается после выявления статистическими методами наиболее значимых показателей ТП шинного производства. Все три описанных способа определения наиболее значимых показателей рекомендуется применять в комплексе. Вначале эксперты устанавливают предварительный перечень показателей, используя рекомендации, разработанные в результате проведенных научных исследований. Для этого предварительного перечня применяют статистические методы, в результате чего выявляется оптимальность, избыточность или недостаточность использованных показателей. При избыточности числа показателей отбрасывают наименее значимые. При недостаточности вновь собирают экспертов, которые решают, какие неучтенные ранее показатели ввести в рассмотрение. Таким образом, процесс повторяется до достижения оптимума. Как уже отмечалось выше, оптимум может определяться разумным соотношением доли неучтенных (фоновых) факторов и сложностью организации автоматизированного измерения контролируемых параметров. (Безусловно, контроль всех N возможных параметров был бы идеальным решением проблемы, но, очевидно, это дорого). Изложим кратко некоторые математические соотношения, позволяющие установить количественную связь между критериями качества шин и параметрами ТП. Проблема выбора адекватной регрессионной модели ТП достаточно подробно описана в литературе [[287]]. Отметим лишь, что наиболее часто используют степенные зависимости, начиная с наиболее простой линейной модели без учета взаимодействия параметров. Это во многих случаях оказывается оправданным, если колебания DA i малы по сравнению с величинами Ai. Однако для решения статистическими методами задач оптимизации параметров модели уравнения должны содержать не только линейные члены. Это требование обусловлено следующими очевидными соображениями. Многие показатели качества шины имеют экстремальный характер. Например, дисбаланс шины ухудшается при отклонениях длины протектора от оптимального значения как в одну, так и в другую сторону. Следовательно, указанная зависимость не может быть линейной. Для ее описания требуется полином не менее чем второй степени. Если, кроме того, имеется влияние значения какого-либо параметра на степень влияния на показатели качества других параметров, то следует использовать члены с произведениями взаимосвязанных параметров. Запишем уравнения для полиномиальной модели с учетом парных корреляций второй степени:
(j = 1, 2, …, M). Cij - численные коэффициенты, подлежащие определению. Нетрудно показать, что соотношение для числа коэффициентов Nc имеет вид:
Чтобы решить каждое из М уравнений (5.3.1), т.е. найти коэффициенты Сij, поступают следующим образом. Для L испытываемых шин определяют показатели Аi (i=1,..., N*) и Bj (j=l,...,М) и для каждой шины под номером s (s=1,..., L) записывают систему уравнений, линейных относительно Сij:
(s=1, …, L) Общее число испытанных шин L должно удовлетворять двум условиям: 1) L должно представлять существенную выборку (напомним, что существенной, или репрезентативной, считается такая выборка, все используемые моменты которой отличаются от моментов генеральной функции распределения не более чем на некоторую допустимую величину [274]); 2) L» Nc. Первое из указанных требований обусловлено необходимостью знания статистических характеристик (моментов) «случайных» величин Аi и Bj (среднее значение, дисперсия, и т.д.), второе необходимо для решения системы (5.3.3) с использованием метода наименьших квадратов [286]. Для определения Сij требуется решить систему L линейных алгебраических уравнений. Так как L достаточно велико (до нескольких сотен), то необходимо использование компьютерных методов. На вычислительных подробностях здесь останавливаться не представляется возможным. Отметим лишь, что используемые методы в достаточной степени стандартные. После определения коэффициентов Сij осуществляется процедура контроля правильности их определения (достаточности показателей ТП, входящих в число N*). При этом используются критерии экстремальности, симметрии, и др. Например, если в соотношение (5.3.3) подставить «идеальные» значения показателей Аi, то соответствующая величина Bj должна стать экстремальной (если Bj - один из показателей силовой неоднородности шины, то Bj ® 0). С помощью уравнений (5.3.3) может быть проведено сравнение теоретических предсказаний о степени и характере влияния тех или иных показателей ТП на качество шины с результатами статистического обобщения эксперимента. Могут быть определены пределы изменения Аi, при которых влияние Аi на Bj описывается линейной зависимостью. Те члены уравнения (5.3.3), которые имеют малые коэффициенты, могут в дальнейшем не учитываться, что упростит систему (5.3.3) за счет уменьшения числа членов. Остановимся более подробно на практически важной проблеме установления допустимых значений DA i колебаний параметров A i, при которых колебания DBj критериев выходного контроля качества Bj не будут выходить за пределы установленных норм. В настоящее время существует и повсеместно используется система жестких норм контроля. Очевидно, что чем меньше разброс показателей ТП, тем более стабильными будут показатели, характеризующие качество готового изделия. Опыт показывает, что в рамках реального производственного процесса на шинных заводах редко можно обнаружить шину, в процессе изготовления которой не было нарушено ни одной нормы. Вместе с тем по результатам выходного контроля основная часть продукции удовлетворяет предъявленным требованиям. Это свидетельствует о том, что система жестких допусков (СЖД) не всегда адекватна качеству изделия. Приведем наглядный пример. Допустим, масса заготовки протектора несколько ниже допустимого значения. Однако общая масса шины осталась в требуемых пределах за счет увеличения калибра обрезиненного металлокордного полотна и увеличения массы других деталей конструкции шины в допустимых пределах. Пример иллюстрирует важность использования не жестких отдельных критериев и их допусков, а системы связанных допусков (ССД), обеспечивающих требуемое качество изделия в целом. Использование ССД потребует в рамках автоматизированного шинного производства осуществление контроля не только «внешних» параметров (давление, температура, калибры и т.п.), но и свойств материалов - полуфабрикатов. Для приведенного выше примера о компенсации массы шины это означает, что потребуются показатели, характеризующие, например, зависимость вероятности отслоения протектора от брекера от колебаний размеров последних при эксплуатации шины. О проблеме адекватного контроля качества материалов-полуфабрикатов мы говорили выше. Использование ССД имеет еще одно важное преимущество перед СЖД. Если в СЖД нарушение одного из допусков в процессе производства автоматически приводит к отбраковке данного изделия, то в ССД остается возможность оперативного вмешательства в дальнейший ТП с целью исправления (компенсации) создавшегося положения. Такая компенсация возможна исключительно на основе высокоавтоматизированного производства с компьютеризацией на всех уровнях, причем выработка управляющего сигнала (рекомендации) должна осуществляться быстро, в масштабах реального времени. Вернемся к соотношениям (5.3.1) и посмотрим, как на их основе создать ССД. После определения коэффициентов Сij будем считать переменными величинами A i. Используем то обстоятельство, что величины Bj имеют экстремальный характер. Этого всегда можно добиться введением комплексных критериев (целевых функций или функционалов, см. (6.4.1)). Тогда задача подбора величин Ai сводится математически к решению системы уравнений для частных производных Bj по A i:
Из уравнений (5.3.4) определяются оптимальные значения Аi opt, при которых критерии качества Bj являются наилучшими - Bj. opt (Мы здесь опускаем вопрос о возможности существования нескольких экстремумов при близких значениях Аi). Понятно, что отклонение DA i от Аi opt приведет к изменению Bj на DBj. Максимально допустимые отклонения показателей, характеризующих качество шины, DB [8] j max будем считать заданными. Возникает вопрос: каково максимальное значение DA i max, при котором оптимальное значение Bj. opt изменится на величину, не превышающую DBj max? Ответ можно получить, воспользовавшись уравнениями (5.3.1). Будем считать переменными все Ai, кроме одной с номером q, для которой зададим некоторое значение Аq = Аq opt + DAq. Далее, как и прежде, решим систему уравнений для производных, аналогичную системе (5.3.4) и найдем все значения Аi opt (i¹q), удовлетворяющие условию экстремальности Bj при некотором фиксированном значении Аq. Повторив описанную процедуру для разных значений Аq, получим ряд значений Bj. Из обработки полученных данных методом интерполяции нетрудно найти DАq max, при котором DBj = DBj max. Поступив подобным образом для всех N* показателей Ai, найдем для каждого из них максимально допустимые отклонения, при которых качество изделия останется в допустимых пределах. Приведенные рассуждения можно повторить не для одного, а для зафиксированных значений двух, трех, и т. д. показателей Ai. При этом можно рассчитать требуемые значения остальных Ai, при которых качество шины будет наилучшим. Смысл изложенного следующий. На основе приведенных уравнений можно рассчитать Аi opt и DА1 max, удовлетворяющие требованиям качества готового изделия. После прохождения того этапа технологического процесса, где контролируются А1, мы имеем реальное значение DА1. Зная это реальное значение, рассчитывается допустимое отклонение DА2 max на втором этапе, которое зависит от DА1. После прохождения второго этапа рассчитывается допустимое отклонение DА3 max при фиксированных А2 и А3, и т. д. В этом и состоит смысл системы связанных допусков. Отметим еще раз, что применение ССД возможно только в условиях автоматизированного производства при наличии системы измерения Ai и передачи данных в компьютерную сеть. При наличии обратной связи (регулирование параметров ТП Ai по командам управляющего компьютера) ССД позволяет контролировать качество и управлять им не только для партии шин, но и для каждой отдельной шины. Теперь обратим внимание на важную специфику шинного производства. Весь ТП условно можно разделить на две части. Первая - изготовление материала (резина и резинокордное полотно), вторая - заготовка деталей, сборка и вулканизация изделия. Преимущество такого разделения в том, что при удовлетворительных значениях показателей свойств материалов можно сделать вывод об общем удовлетворительном состоянии всего ТП до стадии заготовки деталей и сборки. Такой прием называется декомпозицией [4]. Еще одно преимущество декомпозиции заключается в возможности введения промежуточных критериев качества, характеризующих свойства материалов, идущих на изготовление шин. Общая задача сквозного учета влияния всех контролируемых параметров на качество шины делится на две математически сходные, но по числу параметров (и, соответственно, уравнений) существенно более компактные подзадачи, требующие меньшего времени на их решение. Эти две подзадачи, сходные по методам их решения, различаются по набору контролируемых параметров Ai. На втором этапе практически весь контроль сводится к определению геометрических размеров. На первом же этапе необходимо контролировать свойства материалов. Речь об этом шла в разделе 5.2. Изложенный подход апробирован на опытном шинном заводе НИИШП. На основе экспертных оценок проведен отбор наиболее важных показателей, характеризующих ТП шинного производства, в том числе показателей, характеризующих свойства резин и резинокордных деталей конструкции шины. Разработаны регрессионные модели, составлены программы для ЭВМ. Для отработки и практической проверки изложенного подхода к контролю и управлению технологическим качеством в рамках автоматизированного шинного производства были проведены исследования на макете, включающем процесс заготовки деталей, сборки шин, их вулканизации. Для партии около двухсот шин проведены измерения как показателей ТП, так и критериев их качества. Обработка данных показала, что изложенная методология работоспособна. Выявлены показатели, наиболее сильно влияющие на качество шин. Показана возможность оценки стабильности работы заготовительного и сборочного оборудования. Указаны «узкие» места и пути совершенствования производства с целью управления качеством. В заключение раздела можно сформулировать основы системы технологического обеспечения качества продукции для автоматизированного компьютеризированного шинного производства, включающие следующие положения: 1. Экспертный отбор наиболее важных с точки зрения влияния на качество изделия показателей технологического процесса шинного производства. 2. Использование результатов исследований, позволяющих устанавливать связи между показателями ТП и параметрами, характеризующими качество изделия. 3. Применение статистических методов с целью анализа стабильности показателей, характеризующих качество исходного сырья, свойства материалов и полуфабрикатов, работу оборудования, и т. д., а также с целью установления влияния перечисленных факторов на качество готовой продукции. 4. Переход от системы жестких допусков к системе связанных допусков, дающий принципиальную возможность управления качеством шин в процессе производства за счет компенсационных воздействий на последующих стадиях технологического процесса. 5. Применение вышеуказанных пунктов отдельно на стадии изготовления материалов (резина, резинокордные композиты) и на стадии заготовки деталей, сборки и вулканизации. Использование на каждой стадии своих критериев качества. 6. Разработка и использование новых критериев качества материалов, наиболее полно отражающих условия их вулканизации в шинах и условия нагружения в эксплуатации (см. главы 3 и 4). 7. Создание и использование локальной компьютерной сети, выполняющей функции: сбора данных с автоматических датчиков (в исключительных случаях данные могут вводиться вручную оператором); статистической обработки этих данных и передачи их для хранения в базу данных; оперативной обработки текущих показателей технологического процесса с целью выработки (при необходимости) управляющих сигналов для компенсирующей корректировки последующих стадий технологического процесса; оперативного представления информации обслуживающему персоналу и руководству о ходе технологического процесса, отклонениях от нормы и мерах по его стабилизации, и пр. 8. Переход на основе автоматизации и компьютеризации от выборочного к постоянному контролю показателей технологического процесса, что не потребует значительных дополнительных затрат, вместе с тем заметно повысит стабильность качества готовых изделий и повлечет уменьшение числа шин, подвергаемых разрушаемым методам контроля. 9. Максимально возможное исключение субъективного фактора из процесса производства, что также повысит его стабильность и уровень качества.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 488; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.112.220 (0.062 с.) |
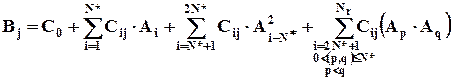 (5.3.1)
(5.3.1) (5.3.2)
(5.3.2) (5.3.3)
(5.3.3) (5.3.4)
(5.3.4)


