
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механика армированных пластиков и резинокордных композитов: монография / каблов В. Ф. , гамлицкий Ю. А. , тышкевич В. Н. – впи (филиал) волггту, волгоград: иунл волггту, 2014 – 341с.
ПРИЛОЖЕНИЕ 1.
Упругий потенциал сплошной несжимаемой среды при больших деформациях может быть с любой точностью записан в виде ряда Муни от первого и второго инварианта I1 и I2 тензора больших деформаций Коши - Грина:
где
Предположим, что с достаточной точностью упругий потенциал может быть записан в виде
который отличается от (П.1.1) отсутствием членов с произведениями инвариантов. Такой вид упругого потенциала обоснован в [[299], [300]]. Для случая задания сложного НДС в виде суперпозиции чистого ly и простого g сдвигов главные удлинения Li (i =1,2,3) определяются из соотношений (2.3.17):
Второе из соотношений (П.1.4) следует из условия несжимаемости среды. Введем новую переменную Перепишем первое соотношение из (П.1.4) с использованием Г:
Полученные с использованием (П.1.5) значения инвариантов (П.1.2) определяются величинами ly и g:
Введем обозначения: J1=I1-3; J2=I2-3. Рассмотрим случай воздействия на единичный образец касательных напряжений, действующих вдоль оси Х. Практически такой вид нагружения может быть реализован на образцах-вилках (рис. 1), если силы, действующие на образец, параллельны. Эта деформация не будет простым сдвигом, т.к. расстояния b0 и b не равны друг другу: b / b0 = ly. Точнее, нет сил, которые сохраняли бы это расстояниенеизменным. Нам предстоит выяснить, как в процессе нагружения образца силой F меняется величина b. Этому вопросу было посвящено несколько работ по той причине, что известен экспериментальный эффект Вайсенберга [[301], 264, с. 37], заключающийся в том, что при сдвиговых деформациях вязкоупругого тела возникают нормальные к направлению сдвига напряжения [36, с. 61]. Первая публикация в этом направлении принадлежит Ривлину [[302]]. Им показано, что при простом сдвиге возникают нормальные напряжения. Рассчитаны и измерены величины этих напряжений для некоторых простых потенциалов. В монографии [264] уделено большое внимание объяснению эффекта Вайсенберга, однако объяснение причин возникновения нормальных напряжений на с. 326-327 содержит существенные неточности, противоречащие описанию деформации простого сдвига на с. 37 той же монографии. В статье [[303]] рассмотрена задача кручения резинометаллического амортизатора для случая больших деформаций. Основной результат состоит в том, что кручение может приводить как к осевому растяжению, так и сжатию цилиндра. В этой же работе утверждается, что Ривлин [302] получил качественно такой же результат. Вполне возможно, что полученные результаты в [303] связаны с тем, что используется линейная теория для описания свойств резины. Как уже говорилось в гл. 1, такой подход не учитывает существенной нелинейности деформационных свойств резин при малых (от 0 до 50%) деформациях. Тем не менее, большинство работ по исследованию механики РТИ и резинокордных слоёв проводится именно в таком приближении [[304]]
Нам не удалось найти в работе [302] подтверждения того, что сдвиг может приводить не только к растяжению, но и к сжатию в нормальном направлении. Кроме того, не вполне ясно, насколько результат зависит от вида используемого упругого потенциала. Предположим, что в рассматриваемом случае деформация в нормальном к оси Х направлении равна ly. Главная деформация L3, направленная перпендикулярно плоскости чертежа, определяется соотношением
С учетом несжимаемости (второе из соотношений (П.1.4)), для главных деформаций L1 и L2 выполняется условие L1×L2 = lу (П.1.8) Величину ly можно определить из соотношения
где U*=U - F×Г. Уравнение (П.1.9) можно решать при разных условиях: при постоянстве величины Г (при этом F будет меняться с изменением lу); при постоянстве силы F (в этом случае Г будет меняться с изменением lу). Подставим в (П.1.9) потенциал (П.1.3) с инвариантами (П.1.6):
= Сила F определяется соотношением:
из которого, с использованием (П.1.3), следует:
Рассмотрим случай, чаще всего реализуемый в эксперименте, когда задается постоянное расстояние между зажимами разрывной машины Г. В этом случае внешняя сила F при изменении ly не совершает работы, поэтому при равновесном значении ly выполняется соотношение
Из (П.1.10) и (П.1.13) получаем:
Проведем дифференцирование:
Разрешить (П.1.15) относительно ly аналитически не представляется возможным. Т.к. наша задача состоит в том, чтобы оценить, будет ли ly больше, равно или меньше единицы, то поступим следующим образом. Допустим, что испытываемый образец состоит из двух параллельных образцов. Плотность энергии деформации одного из них описывается членами, содержащими первый инвариант, а второго – второй инвариант. Тогда соотношение (П.1.15) разобьется на два:
Из (П.1.16) следует: ly = 1 (П.1.18) Из (П.1.17) следует: ly4 = Г2 + 1 (П.1.19) Из (П.1.18) и (П.1.19) очевидно, что суммарная деформация всего образца ly > 1. Кроме того, видно, что максимальное значение ly не может превышать величины, определяемой соотношением (П.1.19). Полученный результат позволяет заключить, что для упругого потенциала вида (П.1.3) при задании деформации простого сдвига Г образец всегда будет стараться увеличить свои размеры по оси Y. Этот вывод не совпадает с результатами работы [303], где с использованием ряда предположений показано, что нормальные размеры образца могут как увеличиваться, так и уменьшаться. Кроме того, из (П.1.18) следует, что неогуковский потенциал (1.2.20) (потенциал Ривлина) не описывает эффект Вайсенберга. Это же утверждение относится ко всем потенциалам, содержащим только первый инвариант (П.1.2).
ПРИЛОЖЕНИЕ 2.
Приведем некоторые математические соотношения, позволяющие из упругого потенциала материала U рассчитывать величины напряжений по главным осям в случаях трех, - двух - и одноосного нагружения. Обычно такие соотношения записывают [36] с учетом явного вида инвариантов I1 и I2 (1.2.14) тензора больших деформаций (1.2.2). Такой способ не является достаточно общим при использовании других инвариантов. Поэтому будем исходить из такого вида упругого потенциала, когда энергия деформации зависит от степеней удлинений по главным осям. В [6] приведен вывод уравнений для общего случая, однако в самом начале введено понятие всестороннего давления p, явно не следующее из строгого рассмотрения уравнений механики больших деформаций. Предлагаемый здесь вывод приводит к тем же результатам, что и в [6], однако он представляется более обоснованным. Единичный кубик деформирован по главным осям силами f1, f2, f3 до размеров l1, l2, l3 ( т.к. кубик единичный, то силы fi являются условными напряжениями, а величины li - и размерами кубика по главным осям, и степенями удлинений одновременно). U(l1, l2, l3) – упругий потенциал материала. Его полный дифференциал:
Приращение энергии кубика при бесконечно малом увеличении величин fi на dfi и величин li на dli (i=1, 2, 3): dU = f1dl1+f2dl2 + f3dl3. (П.2.2) Из сравнения (П.2.1) и (П.2.2) следует
Соотношения (П.2.1 – П.2.3) получены в предположении независимости всех трех li. Введем несжимаемость материала, из которой следует l3=
Соотношение (П.2.1) с учетом (П.2.4) примет вид:
Перепишем (П.2.5):
Соотношение (П.2.6) можно рассматривать в соответствии с (П.2.2) как результат воздействия на искомый образец в виде единичного кубика сил только по двум осям, X и Y, при этом новые условные напряжения
(П.2.7)
U* -та же функция U, но зависящая от двух переменных l1 и l2. Истинные напряжения:
Из соотношений (П.2.8) видно, что истинные напряжения в случае двухосного нагружения выражаются через разности истинных напряжений, действующих в случае эквивалентного трехосного нагружения. Величину Рассмотрим случай одноосного нагружения. При этом степени удлинений по главным осям связаны соотношением
Подставив (П.2.9) в соотношения (П.2.7), получим выражения для условных напряжений
где
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.184.90 (0.029 с.) |
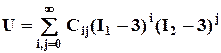 , (П.1.1)
, (П.1.1) ,
, , (П.1.2)
, (П.1.2)

 - степени удлинений по главным осям (главные удлинения).
- степени удлинений по главным осям (главные удлинения). , (П.1.3)
, (П.1.3) . (П.1.4)
. (П.1.4) .
. - величина, пропорциональная перемещению захватов разрывной машины при растяжении образца-вилки (рис. 1).
- величина, пропорциональная перемещению захватов разрывной машины при растяжении образца-вилки (рис. 1). . (П.1.5)
. (П.1.5)
 ;
; 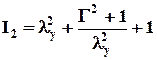 . (П.1.6)
. (П.1.6) (П.1.7)
(П.1.7) , (П.1.9)
, (П.1.9)
 (П.1.10)
(П.1.10)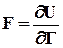 , (П.1.11)
, (П.1.11)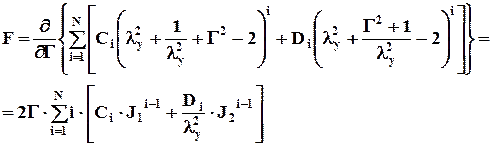 (П.1.12)
(П.1.12) . (П.1.13)
. (П.1.13) (П.1.14)
(П.1.14) . (П.1.15)
. (П.1.15) . (П.1.16)
. (П.1.16) . (П.1.17)
. (П.1.17) . (П.2.1)
. (П.2.1) (i= 1, 2, 3). (П.2.3)
(i= 1, 2, 3). (П.2.3)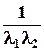 ,
,  ,
,  ,
, . (П.2.4)
. (П.2.4) (П.2.5)
(П.2.5) (П.2.6)
(П.2.6) и
и  имеют вид
имеют вид



 (П.2.8)
(П.2.8)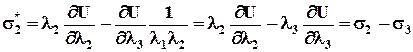
 называют гидростатическим давлением.
называют гидростатическим давлением. . (П.2.9)
. (П.2.9) при одноосном нагружении:
при одноосном нагружении: , (П.2.10)
, (П.2.10) ,
,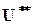 - та же функция, что и U, но с учетом (П.2.9).
- та же функция, что и U, но с учетом (П.2.9).


