
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы описания напряженно-деформированного состояния (ндс) и прогнозирования поведения в эксплуатации резин, резинокордных композитов (ркк) и шинСтр 1 из 22Следующая ⇒
Гамлицкий Юрий Анатольевич УДК 539.313:620.178.3: 678.074 НЕЛИНЕЙНЫЕ МЕХАНИЧЕСКИЕ СВОЙСТВА РЕЗИН И РЕЗИНОКОРДНЫХ КОМПОЗИТОВ И РАБОТОСПОСОБНОСТЬ ДЕТАЛЕЙ ШИН
Технология и переработка полимеров и композитов
МОСКВА - 2014 ОГЛАВЛЕНИЕ ВВЕДЕНИЕ.. 4 1. МЕТОДЫ ОПИСАНИЯ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ (НДС) И ПРОГНОЗИРОВАНИЯ ПОВЕДЕНИЯ В ЭКСПЛУАТАЦИИ РЕЗИН, РЕЗИНОКОРДНЫХ КОМПОЗИТОВ (РКК) И ШИН.. 9 1.1 Введение. 9 1.2 Упругие потенциалы резины.. 13 1.3 Напряжения и деформации резинокордных слоев. 28 1.4 Расчетные и экспериментальные методы и прогнозирование работоспособности. Основные принципы.. 37 1.5 Заключение. Цель работы.. 69 2. УПРУГИЙ ПОТЕНЦИАЛ РЕЗИНЫ И МОДЕЛИРОВАНИЕ СЛОЖНОГО ОДНОРОДНОГО НДС В ЛАБОРАТОРНЫХ УСЛОВИЯХ.. 71 2.1 Упругий потенциал несжимаемого тела для случая изотропности в деформированном состоянии. 71 2.2 Новый подход к построению упругого потенциала наполненной резины 81 2.3 Сложное НДС как суперпозиция чистого и простого сдвигов. 97 2.4 Частный случай простого сдвига. 101 2.5 О возможности построения упругого потенциала по результатам одноосного растяжения-сжатия. 103 2.6 Экспериментально-расчетный метод определения плотности энергии деформации в зависимости от инвариантов деформации. 105 2.7 Свойства резин в сложном НДС.. 111 2.8 Порообразование. Задача Ламе для больших деформаций резины.. 128 3.МОДЕЛИРОВАНИЕ РЕАЛЬНЫХ УСЛОВИЙ НАГРУЖЕНИЯ РЕЗИНОКОРДНЫХ КОМПОЗИТОВ.. 135 3.1 Введение (Напряжения и деформации в каркасе и брекере) 135 3.2 Резинокордные однослойные образцы с «косой» нитью (ОКН). Критерии однородности деформации резины между нитями корда. 137 3.3 Расчет НДС резинокордного слоя. Сравнение с экспериментом. 149 3.4 Соотношения для связи НДС каркаса и брекера с НДС ОКН.. 160 3.5 Различия в механике поведения ОКН с металлическим и текстильным кордами. Расчет НДС ОКН с текстильным кордом. 172 4. МЕХАНИЧЕСКИЕ СВОЙСТВА ОКН И ПОКАЗАТЕЛИ РАБОТОСПОСОБНОСТИ БРЕКЕРА И КАРКАСА ШИН.. 182 4.1 Объекты и методы испытаний. 182 4.2 Результаты прочностных испытаний (растяжение с постоянной скоростью до разделения на части) 187 4.3 Результаты усталостных испытаний. 201 4.4 Характер разрушения ОКН. Различие законов снижения усталостной прочности границы «корд-резина» и резины между нитями корда. 220
4.5 Коммутативность усталостной выносливости. 225 5. КОНЦЕПЦИЯ ПРОГНОЗИРОВАНИЯ РАБОТОСПОСОБНОСТИ ШИН НА СТАДИИ ИХ ПРОЕКТИРОВАНИЯ.. 227 5.1 Общие замечания. 227 5.2 Целевое назначение лабораторных испытаний. 230 5.3 Концептуальные вопросы технологического обеспечения качества. 238 5.4 Схема организации исследований при разработке нового изделия. 249 5.5 Прогнозирование работоспособности резинокордных деталей шин с учетом условий реальной эксплуатации. 260 5.6 Дальнейшие задачи. 268 ЗАКЛЮЧЕНИЕ.. 271 ОСНОВНЫЕ ВЫВОДЫ... 275 Список публикаций автора по теме работы.. 277 ПРИЛОЖЕНИЕ 1. К описанию эффекта Вайсенберга. 293 ПРИЛОЖЕНИЕ 2. Главные напряжения в сложном НДС как производные упругого потенциала. 299 СПИСОК ЦИТИРУЕМОЙ ЛИТЕРАТУРЫ... 302
ВВЕДЕНИЕ
Пневматическая шина представляет собой наиболее массовое и наиболее резиноемкое изделие из всего перечня резинотехнических изделий. В то же время шина - весьма сложная конструкция с точки зрения механики ее нагружения и разрушения. Сложность заключается в том, что резина, в частности, и резинокордный композит (РКК), в целом, подвергаются в процессе эксплуатации большим деформациям, проявляя существенную нелинейность всех механических свойств и релаксационный (вязкоупругий) характер поведения. Являясь анизотропным материалом, РКК работает в условиях сложного напряженно-деформированного состояния (НДС) при негармонических циклических воздействиях со стороны дороги и автомобиля. Перечисленные обстоятельства значительно осложняют возможности применения расчетно-аналитических методов в задачах прогнозирования эксплуатационных характеристик шин. Существующие компьютерные методы используют, как правило, линейный закон для описания свойств резины (в лучшем случае, наиболее простые нелинейные соотношения), что вносит существенные погрешности в результаты расчетов НДС. Оценку долговечности разрабатываемой шины чаще всего производят по величине статического запаса прочности ее резинокордных деталей (здесь и далее не затрагиваются проблемы износа протектора, представляющие собой существенно иную задачу). Такой подход дает определенную информацию о поведении шины в эксплуатации, однако нет уверенности в том, что закономерности, полученные при решении статической задачи, дадут высокую достоверность прогноза в условиях усталостного нагружения. Более того, имеется значительное число экспериментальных данных, из которых следует низкая корреляция между результатами статических и усталостных испытаний.
Вместе с тем хорошо известно, что результаты усталостных испытаний стандартных резиновых или резинокордных образцов также неудовлетворительно дают прогноз поведения шины в эксплуатации. Причину этого следует искать в несоответствии НДС, реализующихся в испытываемом образце и в реальном изделии. Таким образом, представляется актуальной задача разработки теоретико-экспериментальных методов 1) описания сложного НДС резин, наполненных техническим углеродом, и РКК с учетом нелинейности законов деформирования при конечных деформациях и 2) прогнозирования работоспособности (долговечности) резинокордных деталей шины на основе усталостных испытаний образцов, в которых реализуются условия нагружения, близкие к реальным. Это и является основной целью работы. Введение
В первой главе дан обзор существующих методов описания НДС резин и РКК и способы прогнозирования поведения в эксплуатации резинокордных деталей шины. В большинстве работ, посвященных анализу НДС в шине, используется закон Гука, как для нитей корда, так и для резины. Такой подход в свое время был оправдан, т.к. деформации скрещенных резинокордных слоев не слишком велики, что определяется высоким модулем корда при продольном удлинении [[1], [2], [3]]. Кроме того, достаточно простые модели шины не претендовали на высокую точность определения НДС. Ситуация коренным образом изменилась в последнее десятилетие с появлением высокопроизводительной и недорогой вычислительной техники и достаточно прецизионных расчетных схем - многослойные анизотропные оболочки и метод конечных элементов (МКЭ) [[4]]. Теперь узким местом становятся методы описания существенно нелинейных свойств резин [[5], [6]]. В самом деле, из опытов по одноосному удлинению серийных протекторных или брекерных резин следует [см., напр., [7]], что истинный (дифференциальный) модуль меняется в 3 ¸ 5 раз на интервале деформации от 0 до 20% (рис. 1.1.1) (именно в этом интервале, в основном, «живет» шина). Эти результаты (эффект Пейна) получены и для комплексного модуля G* (рис. 1.1.2 - 1.1.3) [[8], [9], [10]].
Рис. 1.1.2 Зависимость G’ от амплитуды деформации при 70°C и частоте 10 Hz для резины на основе каучука SSBR с различным содержанием технического углерода марки N234.
Рис. 1.1.3 Зависимость G’ от амплитуды деформации при 0°C и частоте 10 Hz для резины на основе каучука SSBR с различным содержанием технического углерода марки N234
Осознавая необходимость такого усовершенствования, ряд зарубежных фирм (в частности, Гудьир и Матадор) переходят к использованию методов описания резины, учитывающих ее нелинейность [[11], [12], [13]], ограничиваясь одним из наиболее простых упругих потенциалов - Муни- Ривлина, содержащим две константы.
Тотальное использование МКЭ для всей шины с целью определения наиболее опасных (напряженных) мест в ее конструкции с максимальной степенью детализации в настоящее время и в ближайшем будущем, видимо, не представляется возможным. Кроме того, даже допустив, что такие расчеты возможны, остается неясным, какое место в шине разрушится прежде всего. Ответ на этот вопрос был бы получен, если бы существовала теория усталостной выносливости (или усталостной прочности) резины и РКК. Отсутствие указанной теории ставит на первое место экспериментальные методы исследования усталостных характеристик резин и РКК шины. Здесь также имеются свои принципиальные проблемы. Одна из них состоит в том, что результаты стандартных лабораторных усталостных испытаний резиновых и резинокордных образцов [[14]] плохо коррелируют с поведением шины на стенде или в эксплуатации. Более того, ранжирование резин по их усталостной выносливости, полученное в стандартных испытаниях на многократное растяжение, часто не совпадает с ранжированием в готовом изделии [[15]]. Виной тому, в большой степени, то обстоятельство, что в шине резина работает в условиях сложного НДС, достаточно далекого от условий одноосного нагружения. Из сказанного вытекает следующая проблема: следует разработать такие резинокордные образцы, при усталостном утомлении которых в резине между нитями корда и на границе «корд-резина» возникает НДС, близкое к тому, что реализуется в резинокордных деталях шины. Наконец, актуальной и далеко не тривиальной представляется задача обеспечения достаточной близости технологии изготовления шин и лабораторных резинокордных образцов (в частности, режимов их вулканизации [[16]]), что существенно сказывается на различиях в свойствах резины в образце и в шине. Все изложенное наглядно иллюстрирует необходимость взаимоувязывания на современном этапе (основной чертой которого является повышение требований к качеству шин с целью обеспечения их конкурентоспособности) методов нелинейной механики анизотропных эластомеров, технологии их изготовления и условий эксплуатации в реальном изделии. Только в этом случае можно будет говорить о возможности прогнозирования работоспособности[1] резинокордных деталей шины на стадии ее разработки.
Упругие потенциалы резины
Изложим кратко основные понятия механики деформирования упругого твердого тела, которые понадобятся при переходе к большим деформациям. Классическую теорию малых деформаций рассмотрим на основе фундаментального исследования [[17]]. Положение каждой точки деформируемого тела, определяемое радиус-вектором
а после деформирования
Если использовать общее правило написания сумм, когда суммирование происходит по повторяющимся («немым») индексам, то
Подставив
Поскольку во втором члене индексы k и l являются немыми, можно записать его в симметричном виде
Поменяв местами в третьем члене индексы i и l, получим окончательно
где
Этим выражением определяется изменение элемента длины при деформировании тела. Тензор uik есть тензор деформации; по своему определению он симметричен:
Как и всякий симметричный тензор, uik можно привести в каждой точке к главным осям. Это значит, что можно выбрать такую систему координат – главные оси тензора, - в которой из всех компонент uik отличны от нуля только диагональные компоненты u11, u22, u33. Эти компоненты – главные значения тензора деформации – обозначим как u(1), u(2), u(3). В этом случае элемент длины (1.2.1) примет вид
= где dik – единичный тензор (символ Кронекера). Это выражение распадается на три независимых члена. Это значит, что деформацию можно рассматривать как совокупность трех независимых деформаций по трем взаимно перпендикулярным направлениям – главным осям тензора деформации. Каждая их этих деформаций представляет собой простое растяжение (или сжатие) вдоль соответствующего направления: длина dx1 вдоль первой из главных осей превращается в длину
и аналогично для двух других осей. Величины
представляют собой, следовательно, относительные удлинения ei вдоль этих осей:
В случае малых деформаций из выражения (1.2.4) следует
Закон Гука для малых деформаций записывают в виде
где: sij - тензор напряжений, Е – модуль Юнга, G – модуль сдвига, n - коэффициент Пуассона, eij (i,j = x, y, z)- относительные деформации, через которые тензор деформации выражается в виде
Перепишем в более симметричном виде уравнения (1.2.6) в главных осях:
Введем величину p - гидростатическое давление
Примем условие несжимаемости, из которого следует n = 0.5. Уравнения (1.2.8) примут вид
Наконец, запишем в общем виде выражение для плотности энергии упругого изотропного тела при малых деформациях:
Величины c и m называют коэффициентами Ламэ.
Перейдем к рассмотрению больших (конечных) деформаций. Первой отечественной монографией, посвященной исключительно вопросам механики конечных деформаций, является, видимо, работа [[18]]. Однако первые наброски теории конечных деформаций и попытки ее применения имеются уже в трудах Бусинеска, Сен-Венана, Кирхгофа, Томсона и Тэта и др. (см. литературу в [18]). К настоящему времени опубликовано достаточно большое число монографий по этой проблеме [6, [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29], [30]]. Приведенный список ссылок будет постоянно пополняться в процессе изложения материала.
Ниже изложены основные идеи, сыгравшие ключевую роль в описании упругих свойств эластомеров. Уравнения теории конечной упругости в соответствии с работами [[31], [32], [33]] строятся по принципу аналогии с теорией малых деформаций. В основе этих работ лежит предположение о том, что для случая конечных деформаций могут быть записаны уравнения, аналогичные (1.2.9):
Знак «~» над параметрами указывает на их отличие от случая малых деформаций. Применим уравнения (1.2.11) к случаю одноосного растяжения вдоль оси х под действием приложенного напряжения s*. С использованием (1.2.4) получим:
Здесь li = ei + 1 - степень удлинения по оси i. Из условия несжимаемости l1×l2×l3 = 1 и из полученных выражений следует
Уравнение (1.2.12) представляет основной результат теории Ривлина [31-33]. Другие работы, позволяющие строить теорию упругости для больших деформаций исходя из основных принципов механики (однородность, изотропность, симметрия), нам неизвестны. Вариант такой теории будет предложен в разделе 2.1 Принцип, заложенный в обсуждаемые работы, оказался недостаточно универсальным. Как показали многочисленные эксперименты [[34], [35], [36], 6], уравнения (1.2.12) достаточно хорошо воспроизводят эксперимент только для ненаполненных набухших резин в условиях одноосного растяжения. Причины этого активно анализируются в литературе [[37]], однако обсуждение этого вопроса, связанного с природой молекулярных взаимодействий и структурой вулканизационной сетки, выходит за рамки темы работы. Для изучения свойств материалов в различных условиях нагружения при больших деформациях удобно в качестве исходных использовать не конститутивные уравнения типа (1.2.6) или (1.2.11), а упругие потенциалы. При этом задаются компоненты деформации, а компоненты напряжения получают с помощью упругого потенциала U, представляющего собой в общем случае зависимость плотности энергии деформации от инвариантов тензора деформации [[38], [39], [40]]. Можно показать (см., напр., [36, с. 53-55]), что для главных напряжений справедливы соотношения
где I1 = l12 + l22 + l32 I2 = l12 × l22 + l12 × l32 + l22 × l32 (1.2.14) I3 = l12 × l22 × l32 -
- первый, второй и третий инварианты тензора больших деформаций. Если материал несжимаем (что справедливо для резины, если она работает в условиях, отличных от трехосного деформирования), то I3 = 1 и U – функция только от I1 и I2. В этом случае напряжения определяются с точностью до произвольного гидростатического давления p, потому что это давление не вызывает изменения li. Выражение для главных напряжений примет вид
Полученное соотношение (1.2.15) не является самым общим, т.к. при его выводе использованы инварианты (1.2.14). В Приложении 2 будет приведен вывод для инвариантов любого вида, что может оказаться удобным при решении конкретных задач. Важной и трудной проблемой является нахождение вида потенциала U, достаточно точно описывающего эксперимент. Решать эту задачу можно тремя принципиально различными способами. Первый основан на использовании молекулярно-кинетических представлений об энтропийной природе упругости макромолекул и классической теории высокоэластичности полимерных сеток [37, [41]]. Результатом этой теории является зависимость условного напряжения f при одноосном растяжении от степени удлинения l:
Здесь: К – общее число цепей в образце, k – постоянная Больцмана, Т – абсолютная температура, V0 – объем образца. Если использовать соотношения, связывающие степени удлинения по главным осям li со степенью одноосного удлинения l при условии несжимаемости l1 = l, l2 = l3 = а также связь U с f
то можно получить уравнение состояния резины:
Учет в классической теории высокоэластичности стерических ограничений, приводящих к изменению равновесных размеров макромолекулярных клубков и, соответственно, плотности энергии деформации [[42]] приводит к следующей зависимости:
Еще одним примером использования варианта теории высокоэластичности для построения уравнения состояния сшитого эластомера является работа [[43]], где на основе представлений о наличии внешнего поля, оказывающего механическое воздействие на сегменты макромолекул, составляющих вулканизационную сетку, получен потенциал Хазановича – Бартенева вида
Здесь: m – объем сегмента Куна цепи,
Эксперимент [[44], [45], [46]] показал, что для ненаполненных резин (1.2.19) лучше описывает поведение материала, чем (1.2.18) в области малых и средних деформаций. Причины этого с точки зрения механики будут проанализированы в разделе 2.1. Второй способ построения упругого потенциала для произвольных деформаций основан на принципе аналогии с уравнениями механики малых деформаций, о чем говорилось выше. Добавим к этому, что выражение (1.2.12), проинтегрированное и представленное в инвариантном виде, запишется так:
что совпадает с уравнением (1.2.18), являющимся основным результатом классической теории высокоэластичности [41]. Потенциал (1.2.20) называют «неогуковым». Наконец, третий, наиболее распространенный способ построения упругого потенциала не имеет достаточно строгого обоснования. Он состоит в том, что исследователь, основываясь на каких-либо структурных или иных представлениях, записывает выражение, являющееся комбинацией инвариантов, а параметры этого выражения подбирает эмпирически с использованием, например, метода наименьших квадратов. Перечислим кратко наиболее известные потенциалы. Потенциал Муни [[47]]:
Наиболее общая форма линейной зависимости U от I1 и I2. Потенциал обеспечивает хорошо воспроизводимую на эксперименте линейную зависимость напряжения от деформации при простом сдвиге, но основное его достоинство в практически идеальной воспроизводимости кривых одноосного растяжения ненаполненных резин [[48]], что послужило его широкому распространению при интерпретации как эксперимента, так и различных вариантов теории высокоэластичности, учитывающей топологические и стерические взаимодействия между цепями вулканизационной сетки [37]. При других видах НДС (двухосное однородное растяжение, чистый сдвиг) корреляция с экспериментом слабая. Выражение (1.2.21) часто называют потенциалом Муни - Ривлина, но приоритет принадлежит Муни. Потенциал Черных [6]:
Кроме общего случая, используются варианты при n = 1 или при C2 = 0. На основе большого числа экспериментов в разных условиях нагружения для разных резин показано [[49]], что из потенциалов (1.2.19 – 1.2.22) наиболее предпочтительным является (1.2.22) при n = 1. Потенциал Бидермана [[50]]:
Использовался при расчетах резинотехнических изделий, в частности, шин. Потенциал Исихары и др. [[51]]:
Является частным случаем (1.2.23) при С4 = 0. Большинство из приведенных выше потенциалов представляют собой разное число членов ряда
Кроме перечисленных, использовались следующие выражения. Потенциал Валаниса-Ландела [[52]] (см. также [[53]]):
Один из возможных видов функции Потенциал Огдена [[55]] также представляет собой конкретизацию потенциала (1.2.26):
Потенциал Блатца, Шарды и Чоэгла [[56]]:
Два потенциалаАлександера[[57]]:
Второй потенциал содержит шесть констант и в дальнейшем не будет использоваться нами при расчетах. Частным случаем первого потенциала Александера является потенциал Джента-Томаса [[58]]:
ПотенциалХарт-Смита[[59]]:
Этот потенциал является частным случаем второго потенциала Александера. Некоторые другие виды упругих потенциалов приведены, в частности, в [28], однако они не отличаются принципиально от описанных выше. Попытки построения новых потенциалов предпринимаются и в настоящее время. В работе [[60]] на основе рассуждений о структуре резины (суть данных рассуждений не будем обсуждать, что не входит в задачи обзора) получены выражения, которые автор сравнивает с некоторыми известными потенциалами с использованием опубликованного в литературе эксперимента. В результате этого сравнения оказывается, что выражение для упругого потенциала, содержащее первые три члена ряда (1.2.25), лучше описывает эксперимент, чем то же выражение с добавлением следующего, четвертого члена. Такой результат свидетельствует об ошибках в способе аппроксимации с использованием метода наименьших квадратов, что не вызывает доверия к выводам работы. В работах [[61], [62], [63]] для описания поведения резин в сложном НДС упругие потенциалы с двумя константами строятся на основе результатов испытаний при одноосном растяжении и простом сдвиге. Данный подход дает приемлемые результаты для ненаполненных резин в области средних деформаций. В работах [[64], [65]] предложен метод получения потенциала для более широкой области деформаций. В предположении возможности описания кривой одноосного деформирования полиномом третьей степени автор пришел к потенциалу, изученному Исихарой (1.2.24) в 1951 г., а также к еще двум трехконстантным потенциалам из ряда (1.2.25). Основное утверждение автора состоит в том, что сложное НДС можно описывать на основе закона одноосного растяжения. Это заключение довольно спорное, т.к. при его выводе использованы неочевидные допущения, а экспериментальной проверки не проведено. В разделе 2.5 нами будет показано, что, строго говоря, можно построить бесконечное число разных потенциалов, совпадающих для условий одноосного растяжения. Особенности упругих свойств ненаполненных резин, сшитых в растянутом состоянии, обсуждены в работе [[66]]. Слабоструктурированный в недеформированном состоянии вулканизат растягивали при комнатной температуре, затем окончательно сшивали после релаксации в течение нескольких часов. В приготовленной таким образом резине возникала анизотропия свойств, однако ее проявление можно было обнаружить экспериментально только начиная с деформаций ~ 30%. Этот экспериментальный факт, которому в статье дается объяснение на основе классической теории сеток, будет нами использован в дальнейшем при построении упругого потенциала из соображений симметрии (см. раздел 2.1). В работе [[67]] поставлена задача установления связи параметров трехпараметрического потенциала (1.2.24) с составом резины и структурой сетки. Теми же авторами предпринимаются попытки использовать тот же потенциал для описания вязкоупругих свойств резин [[68]]. Зависимость свойств от скорости растяжения заключена в константы потенциала. Приняв зависимость напряжения при одноосном растяжении от скорости растяжения в виде выражения с одним временем релаксации, вязкоупругую задачу свели к пятиконстантному уравнению. Значения констант определяли методом наименьших квадратов, предварительно разлагая экспоненту в степенной ряд для перевода вязкости из показателя степени в множитель. Аппроксимировали всю кривую растяжения до разрыва. Привели значения констант для разных резин. Безусловно, следует приветствовать попытки [68] построения методов описания вязкоупругих свойств технических резин. Однако хотелось бы утверждения о хорошей точности совпадения расчета с экспериментом подкрепить величиной погрешности в разных диапазонах деформаций и скоростей деформирования и не только при одноосном растяжении. Также хотелось бы понять, почему выбранный вид упругого потенциала лучше многих других, о которых шла речь выше. В работе [[69]] для описания вязкоупругих свойств за основу принята дифференциальная модель, в которой для внутренних переменных записываются эволюционные уравнения. По мнению авторов, эти модели удобнее интегральных в задачах построения эффективных вычислительных алгоритмов, связанных с перестройками сеток в МКЭ в условиях больших деформаций и неоднородных температурных полей. Записаны уравнения, описывающие процессы, происходящие в материале (в рамках предложенной модели). Отличительной чертой модели является отсутствие в записи определяющих уравнений объективной производной от тензора напряжений. В основу релаксационного уравнения положены скорости изменения кратностей упругих удлинений максвелловского элемента материала. При всей обоснованности в [69] исходных посылок, желательно иметь законченные выражения, допускающие практическое использование в расчетных методах типа МКЭ. Для этого следовало бы дать рецепты, аналогично тому, как это сделано в [68], по определению из экспериментов параметров исследуемого материала, причем с учетом вида НДС и с указанием погрешностей. Укажем на еще одну работу по изучению свойств резин в условиях сложного НДС [7]. Автор опирается на результаты эксперимента, из которых следует существенная нелинейность наполненных резин в области малых деформаций. Построение инвариантного выражения для описания свойств в сложном НДС основывается на экспериментах по одноосному удлинению и сжатию. Кроме указанных, используются эксперименты по раздуванию круговой мембраны и закручиванию цилиндра при отсутствии осевой нагрузки. Однако два последних эксперимента используются не для подбора констант потенциала, а для проверки работоспособности полученных выражений. Для равновесного случая получено, что хорошее описание свойств резин, не содержащих активный наполнитель, обеспечивается неогуковым потенциалом (1.2.20). При переходе к наполненным резинам вводится параметр, представляющий собой отношение числа разрушенных техуглерод - каучуковых связей к их общему числу. Далее автор рассматривает случай вязкоупругого поведения материала, записывая уравнения эволюции. Использован интегральный оператор наследственной теории с семью константами. На представленных графиках демонстрируется достаточно хорошее совпадение теории и эксперимента, который включал циклические деформации, релаксацию напряжения и размеров. Правда, не приведены результаты для потенциалов других видов, поэтому трудно судить об оптимальности использованных выражений. Безусловно, все перечисленные потенциалы хорошо себя зарекомендовали для тех материалов и тех условий нагружения, которые интересовали их авторов. Все авторы стремились к наилучшему совпадению с экспериментом во всей области достижимых деформаций. Это оправдано желанием достичь определенной общности результатов, однако, как было указано выше, реальный диапазон деформаций, в котором работают детали РТИ и шин, не превышает 20% и только в критических случаях достигает 50% (например, при наезде шины на препятствие). Нам не удалось найти работ, где совпадение теории и эксперимента исследовалось бы в указанной области (за исключением работы [7], в которой, однако, не проведено сравнительного анализа разных потенциалов). Наличие весьма существенной нелинейности в этом диапазоне (эффект Пейна), связанной с тем, что все технические резины наполнены активным наполнителем (см. рис. 1.1.1 - 1.1.3), обостряет проблему адекватного описания свойств резин при малых деформациях. Даже небольшие погрешности в величине зависящего от деформации модуля могут привести к существенным ошибкам в прогнозе тепловыделения при работе в режиме усталостного утомления и числа циклов до разрушения. Решению задачи построения упругого потенциала технических резин в области малых и средних деформаций посвящен раздел 2.2. Следует отметить, что в некоторых из цитированных работ утверждается, что до 10% деформации высоконаполненные резины ведут себя практически линейно (см., напр., [28], с.71). Эта неточность, видимо, связана с трудностями экспериментального определения напряжений при малых деформациях. Более подробно об этом будет сказано ниже.
Кратко остановимся на экспериментальных методах, используемых при изучении упругих свойств резин в сложном НДС [42-44, [70], [71], [72],[73], [74]]. Рис. Образцы и дополнительное оборудование, используемое для получения данных о свойствах резин элементов конструкции шины
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 857; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.161.132 (0.11 с.) |

 Рис. 1.1.1 Зависимости напряжения и модуля от величины одноосного растяжения для резин ненаполненных и наполненных активным наполнителем.
Рис. 1.1.1 Зависимости напряжения и модуля от величины одноосного растяжения для резин ненаполненных и наполненных активным наполнителем.

 с компонентами x1=x, x2=y, x3=z, после деформации имеет радиус-вектор
с компонентами x1=x, x2=y, x3=z, после деформации имеет радиус-вектор  с штрихованными компонентами. Смещение точки тела изображается вектором деформации
с штрихованными компонентами. Смещение точки тела изображается вектором деформации  с компонентами
с компонентами  . Рассмотрим две бесконечно близкие точки с радиус-вектором между ними
. Рассмотрим две бесконечно близкие точки с радиус-вектором между ними  . Его длина до деформирования определяется соотношением
. Его длина до деформирования определяется соотношением


 ,
,  .
. 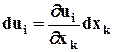 , переписываем
, переписываем  в виде
в виде
 .
. , (1.2.1)
, (1.2.1) . (1.2.2)
. (1.2.2) . (1.2.3)
. (1.2.3)
 ,
,
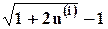 (1.2.4)
(1.2.4)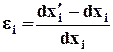 .
. . (1.2.5)
. (1.2.5)
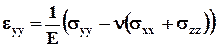

 (1.2.6)
(1.2.6)

 ,
, (1.2.7)
(1.2.7)
 (1.2.8)
(1.2.8) .
.
 (1.2.9)
(1.2.9) (1.2.10)
(1.2.10) . (1.2.11)
. (1.2.11)

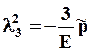
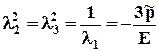 ;
;  ;
; (1.2.12)
(1.2.12) (i=1,2,3), (1.2.13)
(i=1,2,3), (1.2.13) . (1.2.15)
. (1.2.15) . (1.2.16)
. (1.2.16) , (1.2.17)
, (1.2.17) ,
,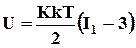 (1.2.18)
(1.2.18) (1.2.18-1)
(1.2.18-1) . (1.2.19)
. (1.2.19) - среднее значение относительного удлинения цепи в недеформированном состоянии.
- среднее значение относительного удлинения цепи в недеформированном состоянии. , (1.2.20)
, (1.2.20) . (1.2.21)
. (1.2.21) . (1.2.22)
. (1.2.22) . (1.2.23)
. (1.2.23) . (1.2.24)
. (1.2.24) (Соо = 0). (1.2.25)
(Соо = 0). (1.2.25)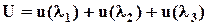 . (1.2.26)
. (1.2.26) использован в работе [[54]].
использован в работе [[54]].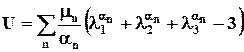 (1.2.27)
(1.2.27) (1.2.28)
(1.2.28) (1.2.29)
(1.2.29)
 . (1.2.30)
. (1.2.30) (1.2.31)
(1.2.31)


 Двухосевая универсальная испытательная машина Zwick. Измерение деформаций и управление режимом деформирования можно осуществлять как по перемещению захватов, так и видеодатчику videoXtens, который отслеживает положение меток на образце
Двухосевая универсальная испытательная машина Zwick. Измерение деформаций и управление режимом деформирования можно осуществлять как по перемещению захватов, так и видеодатчику videoXtens, который отслеживает положение меток на образце Образец типа «большая гантель» по ГОСТ 17443-72 для определения усталостных свойств резинокордных композитов
Образец типа «большая гантель» по ГОСТ 17443-72 для определения усталостных свойств резинокордных композитов


