
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Резинокордные однослойные образцы с «косой» нитью (ОКН). Критерии однородности деформации резины между нитями кордаСодержание книги
Поиск на нашем сайте
Анализ литературы, приведенный в главе 1, позволил заключить, что для решения практических задач следует искать компромисс - создавать образцы для лабораторных испытаний резинокордных композитов, в которых, с одной стороны, реализуется НДС, близкое к реальной ситуации в шине, а с другой стороны - допускающие достаточно строгое применение расчетно-экспериментальных методов для задания нужного НДС и адекватной обработки результатов испытаний. В конечном итоге идеальной представляется такая ситуация, когда результаты простых лабораторных испытаний специальных резинокордных образцов позволяют с высокой степенью достоверности прогнозировать поведение в эксплуатации резинокордных деталей конкретной шины в конкретных условиях. Для решения этой задачи – максимум необходимо использовать такой резинокордный образец, который удовлетворял бы следующим условиям:
1. Конструкция образца должна быть по возможности приближена к конструкции деталей брекера и каркаса шин. 2. Условия нагружения образца должны отражать условия нагружения брекера и каркаса шин. 3. На одном типе образца требуется определять равновесные, динамические и предельные характеристики. 4. НДС образца должно быть достаточно однородным для обеспечения возможности пересчета характеристик образца на характеристики резинокордных деталей шины. 5. Конструкция образца должна обеспечивать высокую точность задания параметров нагружения и определения результатов испытаний. 6. Образец должен быть прост в изготовлении. 7. Должна иметься возможность заготовки того же типа образца из шин. 8. Должна быть предусмотрена возможность одновременной установки на машины для усталостных испытаний (УР-500, МРС-2, ММР и др.) большого числа образцов (до 24) с целью сокращения затрат и уменьшения времени на проведение усталостных испытаний. 9. Образец не должен быть массивным для обеспечения высокой однородности вулканизационной сетки.
Всем указанным требованиям в большой степени удовлетворяет резинокордный образец, представляющий прямоугольный фрагмент резинокордного слоя. Его конструкция отражает конструкцию РКК в шине, т.к. образец заготавливается из того же резинокордного полотна, которое используется в производстве исследуемой шины. Он прост в изготовлении и, как мы увидим ниже, позволяет с высокой степенью точности воспроизводить то НДС, которое возникает в шине при ее эксплуатации. Один и тот же образец может быть использован в статических, динамических и усталостных испытаниях.
Он имеет небольшую толщину, что позволяет гарантировать однородность степени вулканизации по всему массиву образца и использовать специальные вулканизационные прессы с переменной температурой вулканизации. Кроме НДС резины между нитями корда и нормальных и касательных напряжений на границе «корд-резина», образец своей боковой поверхностью имитирует кромку брекера шины, которая является одним из наиболее уязвимых мест шины с точки зрения возникновения очага усталостного разрушения. Общий вид образца приведен на рис. 3.2.1. При проведении испытаний образец закрепляется в зажимы испытательной машины так же, как это делается для полоски резины. Для определения величины его общей деформации при упруго-прочностных испытаниях следует использовать экстензометр – устройство для определения величины растяжения образца в области однородного деформирования. Следует отметить, что неоднородности, связанные с концевыми эффектами, простираются в этих образцах существенно дальше от зажимов, чем неоднородности при испытаниях резиновых полосок. По этой причине размер рабочего участка, как правило, существенно меньше расстояния между зажимами испытательной машины. Вид образца,
а) б)
Рис. 3.2.2 Вид образца ОКН: а) - до деформирования, б) - в растянутом виде.
который закреплен в зажимы и растянут, представлен на рис. 3.2.2. Образцы, заготовленные из одного и того же материала (резинокордного полотна) могут отличаться один от другого величиной угла j, характеризующего наклон нитей корда к продольной оси образца (рис. 3.2.1). Это отличие принципиальное и является центральным местом при реализации возможности воспроизведения на образце того НДС, которое возникает в шине при ее эксплуатации. По этой причине предлагаемые для лабораторных испытаний резинокордные образцы- полоски названы образцами с «косой нитью» (ОКН). В самом деле, в образцах с поперечным расположением нитей корда (j = 900) НДС резины между нитями корда является чистым сдвигом[5], а касательные напряжения на границе «корд-резина» равны нулю. В общем случае (j ¹900) НДС резины представляет собой суперпозицию чистого и простого сдвигов, при этом на границе «корд-резина» действуют и касательные, и нормальные напряжения и деформации и их соотношение зависит от величины угла j.
Перечислим предположения, которые нами используются в дальнейшем. Будем предполагать, что деформация резины между нитями корда является однородной. Уточним, что однородность между нитями корда может нарушаться по двум причинам: из-за взаимодействия резины с поверхностью корда и из-за наличия края резинокордной полоски, представляющей ОКН. Вторая причина многократно обсуждалась в литературе (см., напр., [4]). Она напрямую связана с реализацией чистого сдвига. Ее вклад тем меньше, чем больше отношение длины нитей корда к расстоянию между нитями. Первая причина нарушения однородности, на первый взгляд, представляется существенной из-за того, что расстояние между нитями корда примерно равно толщине резинового слоя (или диаметру нити). В дальнейшем мы проверим, насколько наше предположение об однородности НДС соответствует действительности. Примем также, что в процессе деформирования ОКН в зоне рабочего участка сохраняется прямолинейность нити корда. Это предположение отчетливо подтверждается экспериментально (рис. 3.2.2). Но, строго говоря, если принять несущественной вторую возможную причину нарушения однородности, то прямолинейность нитей корда следует из этого автоматически. В этом случае нет причин, которые привели бы к искривлению нитей при деформировании. Тем не менее, имеются работы по механике деформирования резинокордных слоев [99], из которых следует существенное отклонение от прямолинейности. Первое свидетельство в пользу правомерности предположения о высокой степени однородности НДС резины между нитями корда при растяжении ОКН визуально следует из рис. 3.2.2. Отчетливо видна плоская поверхность резины между нитями корда, что может быть только при однородной деформации. Количественно степень однородности будет оценена ниже из более строгих соображений. Следующее предположение состоит в том, что при растяжении ОКН нити корда считаются нерастяжимыми. Это является следствием того, что при нагружении ОКН нити корда не испытывают тех максимальных нагрузок, которым они подвергаются в шине. В ОКН воспроизводятся условия нагружения резины между нитями корда, но не самих нитей. В настоящее время практически не наблюдаются дефекты, связанные с низкой прочностью корда, и в данной работе эта проблема не рассматривается. С учетом низких нагрузок на нить в ОКН[6] и на несколько порядков более высоких значений модуля корда при растяжении, чем модуля резины, это предположение не вызывает сомнений при рассмотрении металлокорда. Для образцов с текстильным кордом ниже будут выведены соотношения, из которых следуют ограничения на значения параметров образца, при которых нить корда испытывает растягивающие или сжимающие нагрузки. С учетом всего сказанного выведем соотношения, связывающие структуру образца и степень его растяжения с деформацией резины между нитями корда. Введем следующие обозначения (рис. 3.2.3):
h - расстояние между осями нитей корда b - ширина образца
j - - угол между нитями корда и направлением растяжения образца d0 - диаметр нити корда и исходная толщина образца l - - степень растяжения всего образца. Индекс «0» относится к недеформированному состоянию, т.е. при l = 1. Из условия аффинности деформации образца в целом найдем величину деформации резиновой прослойки в нормальном направлении ln. Эта деформация является чистым сдвигом, так как ширина резиновой прослойки, равная длине нити корда, остается практически неизменной. Очевидно, что c = l × c0. Легко показать, что выражение для ln резиновой прослойки имеет вид (рис. 3.2.3)
где Соотношение (3.2.1) связывает ln с параметрами образца и измеряемыми значениями b и l. Здесь следует уточнить, что степень сокращения ширины образца b/bo не является, строго говоря, независимым параметром. Она определяется упругим потенциалом резины, минимум которого при заданной степени удлинения всего образца связан со значением b/bo = sin j / sin jo. Однако на данной стадии изложения будем этот параметр считать экспериментально определяемым. В следующем разделе мы вернемся к этому вопросу. Деформирование резиновой прослойки между нитями корда в тангенциальном направлении является простым сдвигом. Будем его величину характеризовать, как принято [4], тангенсом угла сдвига g. Из рисунка 3.2.3 также следует:
где Растягивающая нагрузка Р раскладывается на две составляющие - нормальную Рn и касательную Рt, каждая из которых создает соответствующие условные напряжения sn и st (рис. 3.2.1): Рn = Р×sinj, Рt = Р×cosj, (3.2.3)
Отметим, что напряжение определяется делением нагрузки не на площадь перпендикулярного к продольной оси сечения образца, а на площадь сечения, расположенного параллельно направлению нитей корда. Это в большей мере отражает реальные процессы нагружения и разрушения резины между нитями корда. Полученные соотношения позволяют строить зависимости sn(ln) и st(g), которые требуются не только для оценки свойств материала, но и для расчета вновь разрабатываемых изделий (в частности, шин) на стадии их автоматизированного проектирования. Вернемся теперь к вопросу описания свойств резины между нитями корда на основании результатов испытаний ОКН. Одновременно проверим справедливость предположения об однородности деформирования резины между нитями корда.
Покажем, что суперпозиция чистого и простого сдвигов может быть частным случаем простого растяжения при достаточно сложной зависимости между направлениями главных осей в том и другом случаях.
Рис.3.2.4 иллюстрирует данное утверждение. При одноосном растяжении фрагмент резинового образца, имеющий в недеформированном состоянии форму прямоугольника (рис. 3.2.4-а), преобразуется в параллелограмм (рис. 3.2.4-б). При деформировании ОКН прямоугольный фрагмент между нитями корда также преобразуется в параллелограмм (рис. 3.2.3). Если в результате деформирования равные прямоугольники преобразуются в равные параллелограммы, то можно утверждать, что при простом растяжении резиновый образец пришел в то же состояние, что и ОКН при суперпозиции чистого и простого сдвигов. Приведем выкладки, позволяющие установить количественные соотношения между указанными случаями. При одноосной степени удлинения L резинового образца деформации по осям имеют значения: L1 = L, Запишем некоторые соотношения между параметрами прямоугольника и параллелограмма (рис. 3.2.4):
y = L × sinb x = L × cosb y0 = L0 × sinb0 x0 = L0× cosb0 (3.2.5)
Жесткость корда приводит к условию:
Из соотношений (3.2.5) и (3.2.6) следует:
Сравнивая соотношения (3.2.1) и (3.2.2) с (3.2.7), а также рис. 3.2.3 и рис. 3.2.4 видим, что
Найдем связь ln с L. Из условия несжимаемости резины при деформировании следует (рис. 3.2.4) L0 ×B0 ×D0 = L× B ×D, где D - толщина образца. Используя (3.2.6), получим B 0 ×D0 = B ×D Толщина образца D при деформировании меняется в соответствии с (3.2.4):
С учетом этого
Таким образом, степень деформирования резины в ОКН в нормальном направлении ln связана со степенью удлинения резины при простом растяжении L:
Из (3.2.7) и (3.2.8) следует связь между g и L:
Итак, при выполнении условий (3.2.9) и (3.2.10) можно утверждать, что НДС резины при одноосном растяжении и резины между нитями корда в ОКН одинаковы, т.е. резина между нитями корда в ОКН находится в состоянии одноосного растяжения. Из соотношений (3.2.1), (3.2.2), (3.2.9), (3.2.10) можно получить связь между степенью растяжения ОКН l и степенью одноосного растяжения резины L:
(3.2.11)
Систему уравнений (3.2.11) решали численно методом Ньютона-Рафсона. Из найденных корней lk отбирали действительные, удовлетворяющие условиям: lk > 1, L(lk) > 1. Таким образом, НДС резины при величине одноосного растяжения L = L(lk) и НДС резины между нитями корда в ОКН при l = lk совпадают. При условии однородности НДС в ОКН плотность запасенной энергии в двух образцах должна быть одинаковая. Испытания проводили на образцах резины и ОКН, заготовленных из одного полотна обрезиненного металлокорда. Экспериментальные результаты следующие. ОКН, заготовленный из слоя брекера, резина 2э-2189, корд 9л15/27, с параметрами (см. рис. 3.2.3): j0 = 600, h0/d0 = 1.8/0.83, lокн = 1.58 и резина, растянутая до величины L = 2.12, должны иметь одинаковую плотность энергии деформации при условии полной однородности НДС резины между нитями корда. При квазиравновесных испытаниях на модульной рамке (40 экспериментальных точек за 20 суток) получено: U окн = 1.57 МДж/м3, Uрезины = 1.63 МДж/м3. Различие составляет менее 5%, что свидетельствует о высокой степени однородности НДС между нитями корда. Далее, в условиях одноосного растяжения только одно из главных напряжений отлично от нуля. Эксперименты показали, что в резиновом образце это напряжение равно 2.68 МПа, а в ОКН - 2.36 МПа. Различие составляет ~ 12%. Эта величина превышает погрешность измерений. Видно, что и для энергии и для напряжения соответствующие величины в ОКН несколько ниже, чем в резине. Объяснение этому состоит в том, что в расчетной модели нить корда имеет сечение квадратной формы с размером стороны, равным диаметру нити корда. Если размер стороны этого квадрата принять таким, чтобы резиносодержание в ОКН соответствовало резиносодержанию в реальном резинокордном полотне, то сопоставимые значения lокн и lрезины будут отличаться от приведенных выше и значения напряжений в резине и в ОКН составят: 2.44 МПа и 2.52 МПа.
Но, видимо, наиболее убедительное подтверждение гипотезы об однородности будет продемонстрировано в следующем разделе, где приводится сопоставление результатов эксперимента и расчета для ОКН с различными углами j. В расчете будут использованы потенциалы, подробно описанные в главе 2.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 558; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.18.255 (0.011 с.) |




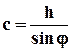 -расстояние между осями нитей вдоль направления растяжения образца
-расстояние между осями нитей вдоль направления растяжения образца , (3.2.1)
, (3.2.1) .
. (3.2.2)
(3.2.2)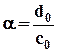 .
.

 (3.2.4)
(3.2.4) x = L × x0
x = L × x0 x = L × L0× cosb0
x = L × L0× cosb0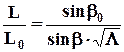
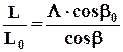
 (3.2.6)
(3.2.6)
 (3.2.7)
(3.2.7)

 ,
,  . (3.2.8)
. (3.2.8)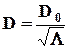 .
.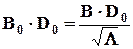 ,
,  .
. . (3.2.9)
. (3.2.9) (3.2.10)
(3.2.10)




