
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Соотношения для связи ндс каркаса и брекера с ндс окнСодержание книги
Поиск на нашем сайте
В предыдущем разделе показано, что резинокордные образцы с «косой нитью» (ОКН) позволяют воспроизводить условия сложного НДС, возникающего в шине при ее эксплуатации. В настоящем разделе излагается расчетный метод определения НДС резины между нитями корда в слое каркаса или брекера. В качестве исходных данных используются результаты экспериментального (например, тензометрический [121] или поляризационно-оптический [119] методы) или расчетного определения эффективных деформаций данной детали шины при ее нагружении. Приводятся соотношения, позволяющие найденное сложное НДС воспроизводить на образцах типа ОКН.
Как уже было отмечено в разделе 3.1, условия нагружения деталей шины и ОКН не являются тождественными. Одна из основных причин этого состоит в том, что в каркасе и брекере шины корд испытывает значительные растягивающие нагрузки. В ОКН при всех практически реализуемых значениях угла j нагрузка на нить пренебрежимо мала. Однако это обстоятельство не исключает возможности воспроизведения на ОКН «шинного» НДС, т.к. суперпозиция чистого и простого сдвигов может обеспечить любое НДС, характеризуемое произвольным соотношением удлинений по главным осям[7]. Исходными данными для каркаса шин радиальной конструкции являются значения меридионального относительного удлинения eмер., окружного eокр. и удлинения под углом 45° к меридиану (схема расположения датчиков деформации дана на рис. 3.4.1)
Требуется рассчитать величину угла jо между продольной осью ОКН и направлением нитей корда при отсутствии внешней нагрузки и величину деформации eокн, при которых НДС ОКН будет совпадать с НДС слоя каркаса, изображенного на рис. 3.4.1. При этом должны совпадать значения нормальной sn и тангенциальной st составляющих напряжения s в шине и образце (рис. 3.2.1). Общая идея следующая. Для получения НДС в резине между нитями корда ОКН, аналогичного НДС между нитями корда в шине, следует добиться, чтобы деформации по главным осям в шине и ОКН совпадали. После этого направления главных осей в ОКН следует задать такими, чтобы совпали sn и s t в ОКН и в шине. Заметим, что направления главных осей в ОКН и в шине не совпадают из-за того, что в шине возможна заметная деформация корда в отличие от ОКН, где размеры образца таковы, что, как правило, существенного удлинения нитей корда не происходит.
Введем обозначения: lокр. = l0окр×·lокр. - длина датчика деформации, расположенного в исходном состоянии в окружном направлении; l0окр × - исходная длина этого датчика; lмер. = l0мер.·lмер. - то же в меридиональном направлении; l45 - то же для направления под углом 45° к меридиану. Для удобства начальная длина датчиков имеет величины: l0окр. = l0мер. = Положения датчиков на боковой поверхности шины или непосредственно на слое каркаса или брекера (в соответствии с рис. 3.4.1) схематично изображены на рис. 3.4.2. Ось X всегда совпадает с направлением нитей корда, ось Y лежит в плоскости резинокордного слоя. Таким образом, для каркаса радиальных шин в исходном состоянии ось X совпадает с меридиональным направлением, ось Y - с окружным.
Из рис. 3.4.2 легко получить соотношения:
lокр. = l0окр×·lокр.= l0окр×·(eокр.+1) (3.4.2) lмер. = l0мер.·lмер.= l0мер.·(eмер..+1) l45 = l045·l45 = l045.·(e45+ 1) Из теоремы косинусов и из рис. 3.4.2 следует:
(Применение геометрических соображений основано на гипотезе однородности деформирования элемента шины по месту расположения датчиков деформации). Из (3.4.3) с учетом (3.4.1) и (3.4.2) можно определить значение угла q, характеризующее величину простого сдвига резинокордной детали шины
Степень удлинения в нормальном (окружном) направлении ly определяется соотношением:
Степень удлинения в меридиональном направлении lx:
Из рис. 3.2.3 и рис. 3.4.2 следует связь величины g = tgq, характеризующей величину простого сдвига всего резинокордного слоя, с величиной gрез. = tgqрез. , характеризующей величину простого сдвига в резине между нитями корда:
Для воспроизведения НДС в шине на образцах типа ОКН требуется выполнение соотношений: L1 окн =L1 шин (3.4.8) L2 окн =L2 шин
где L1 и L2 - удлинения по главным осям резины в ОКН и в шине между нитями корда. Определение направлений главных осей и главных удлинений резины между нитями корда в ОКН и в шине проведем по аналогии со способом, предложенным и реализованным в разделе 2.3. Отличие будет состоять в том, что, как уже отмечалось, в шине нельзя пренебрегать удлинением нитей корда в процессе нагружения. Это приводит к необходимости добавления деформации по оси Х, т.е. вдоль направления нитей корда.
Введем единичный вектор i, расположенный под углом y к нормали нити корда (рис. 3.4.3). После деформирования i перейдет в i ¢. Длина i ¢ зависит от y. Требуется найти значения y и y¢, при которых | i ¢ | имеет максимальное и минимальное значения. Известно, что Исходные проекции i на оси координат:
В результате деформации чистого сдвига lx и ly по осям х и у проекции вектора i принимают значения
Деформация g простого сдвига по оси x, приложенная после чистых сдвигов, приводит к соотношениям:
Квадрат длины вектора i ¢ определяется соотношением, следующим из (3.4.11):
Условие экстремума для длины вектора i ¢:
Продифференцировав выражение (3.4.12), получим:
Из (3.4.14) найдем значение угла y, при котором
Направления главных осей определяются углом y¢ (рис. 3.2.5), который связан с углом y соотношением:
Из (3.4.15) можно получить значение для tgy:
где Подставив (3.4.17) в (3.4.16), получим
Как и следовало ожидать, направления главных осей зависят только от величины a, но не от lx и ly в отдельности. Перпендикулярность осей следует из соотношений: tgy1× tgy2= -1 tgy1¢× tgy2¢= -1 (3.4.19) Справедливость соотношений (3.4.19) для y и y¢ легко проверяется подстановкой (3.4.17) и (3.4.18) в (3.4.19). Соотношение (3.4.18) дает направления главных осей как для элемента шины, так и для ОКН, только в последнем случае Удлинения по главным осям L1 и L2 определяются из соотношения (3.4.12), в которое подставлены значения tgy1,2, определенные выражениями (3.4.17). Величина ly, входящая в (3.4.12), связана с нормальной деформацией ОКН
где:
d0 - диаметр нити корда, h0 - расстояние между нитями корда в исходном состоянии, b0 - ширина ОКН в исходном состоянии, b - ширина ОКН в результате деформирования. Зависимость В практических целях можно ограничиться менее строгим подходом – определить зависимость
Значения d для данного резинокордного полотна определяются только величиной j0. Будем считать функцию d(j0) известной.
Рис. 3.4.4 Зависимость
Рис. 3.4.5 Зависимость
С учетом (3.4.21) соотношение (3.4.20) принимает вид:
Из (3.4.22) нетрудно выразить lокн через
Перед корнем следует выбрать знак «-», т.к. в противном случае при d ® 0, Запишем связь величины нормальной деформации резины между нитями корда
Отсюда следует
Величина простого сдвига резины между нитями корда gрез связана с параметрами ОКН и величиной его удлинения соотношением (рис. 3.2.4):
Составляющая простого сдвига всего ОКН g из соотношения (3.4.7) имеет вид:
Подставив (3.4.26) в (3.4.27), получим
Здесь использовано (рис. 3.2.3):
Таким образом, получены все соотношения, позволяющие на образцах типа ОКН воспроизводить деформированное состояние, реализуемое в данной детали шины. Если в шине измерены не деформации, а нагрузки на границе «корд-резина», то для имитации этих нагрузок на ОКН окажутся полезными следующие соотношения: Pn=P×sinj - нормальная составляющая нагрузки P, действующая на границе «корд-резина», Pt=P×cosj - тангенциальная (касательная) составляющая нагрузки P,
(3.4.29)
Используя соотношение (3.4.21) и имея в виду, что
можно варьированием j0 и P получить требуемые значения sn , sn/st. Приведенный в настоящем разделе подробный анализ достаточно строго учитывает все факторы, характеризующие локальное НДС в данном месте слоя каркаса или брекера, и все особенности деформирования ОКН. В реальности, учитывая ограниченную точность тензометрических измерений НДС шины, вполне достаточно ограничиться менее подробной моделью. В частности, можно пренебречь изменением ширины ОКН при деформациях образца 10-15%, соответствующих реальным условиям эксплуатации. Также можно пренебречь растяжимостью нитей корда в шине, особенно в резинометаллокордных деталях, имея в виду, что модуль корда на 2 - 3 порядка выше модуля резины. Погрешности, привносимые указанными допущениями, могут быть оценены экспериментально. Можно утверждать, что использование в полном объеме результатов проведенного исследования будет наиболее эффективно для усовершенствованных методов изучения механики шин, учитывающих нелинейное поведение резины.
Приведем в табл. 3.4.1 примеры применения изложенной теории к шинам.
Таблица 3.4.1 Расчетные параметры образцов для моделирования НДС шин.
Следующим шагом с целью уточнения сложного НДС резины в резинокордных деталях шины будет учет не только продольной жесткости нитей корда, как в настоящем разделе, но и ее поперечной и продольной сдвиговой жесткости, что относится ко всем неметаллическим кордам. Об этом речь пойдет в разделе 3.5.
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 555; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.83.189 (0.007 с.) |


 l045. (3.4.1)
l045. (3.4.1)

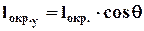
 (3.4.3)
(3.4.3) (3.4.4)
(3.4.4) (3.4.5)
(3.4.5) (3.4.6)
(3.4.6) (3.4.7)
(3.4.7)
 и
и  отличаются на 90°. Эти направления являются главными. Найдем эти направления.
отличаются на 90°. Эти направления являются главными. Найдем эти направления.
 (3.4.9)
(3.4.9)
 (3.4.10)
(3.4.10)
 (3.4.11)
(3.4.11) (3.4.12)
(3.4.12) (3.4.13)
(3.4.13) (3.4.14)
(3.4.14) экстремален:
экстремален: (3.4.15)
(3.4.15) (3.4.16)
(3.4.16) , (3.4.17)
, (3.4.17)
 (3.4.18)
(3.4.18) , т.к. в ОКН растяжимость нитей корда при используемых размерах образцов практически отсутствует. В металлокордных системах можно считать направления главных осей совпадающими для ОКН и шины.
, т.к. в ОКН растяжимость нитей корда при используемых размерах образцов практически отсутствует. В металлокордных системах можно считать направления главных осей совпадающими для ОКН и шины. первым из соотношений (3.4.8). Выведем зависимость удлинения ОКН lокн от нормальной составляющей деформации резины между нитями корда ОКН
первым из соотношений (3.4.8). Выведем зависимость удлинения ОКН lокн от нормальной составляющей деформации резины между нитями корда ОКН  . Из геометрии деформирования ОКН можно получить (рис. 3.2.4):
. Из геометрии деформирования ОКН можно получить (рис. 3.2.4): (3.4.20)
(3.4.20) ,
, от lокн не является геометрически обусловленной величиной. Она определяется свойствами деформируемого материала, т.е. резины между нитями корда. Строго определить эту связь можно из аналитической зависимости плотности энергии деформации резины от инвариантов тензора деформации, что сделано в разделе 3.3.
от lокн не является геометрически обусловленной величиной. Она определяется свойствами деформируемого материала, т.е. резины между нитями корда. Строго определить эту связь можно из аналитической зависимости плотности энергии деформации резины от инвариантов тензора деформации, что сделано в разделе 3.3.
 от eокн для РКК на основе металлокорда 28Л22/15.
от eокн для РКК на основе металлокорда 28Л22/15.
 (3.4.22)
(3.4.22) :
: (3.4.23)
(3.4.23) ®¥, что лишено смысла. Заметим, что из (3.4.20) следует важный вывод: при неизменности b в процессе деформации величина
®¥, что лишено смысла. Заметим, что из (3.4.20) следует важный вывод: при неизменности b в процессе деформации величина  (3.4.24)
(3.4.24) (3.4.25)
(3.4.25) . (3.4.26)
. (3.4.26) . (3.4.27)
. (3.4.27) . (3.4.28)
. (3.4.28)
 - нормальное напряжение на границе,
- нормальное напряжение на границе, - касательное напряжение на границе,
- касательное напряжение на границе, - площадь сечения ОКН, по которому идет разрушение,
- площадь сечения ОКН, по которому идет разрушение, - соотношение нормальных и касательных напряжений на границе «корд-резина».
- соотношение нормальных и касательных напряжений на границе «корд-резина». , (3.4.30)
, (3.4.30) = 1,027
gрез = 0
L1 = 1,027
L2 = 1,007
= 1,027
gрез = 0
L1 = 1,027
L2 = 1,007
 = 1,034
= 1,034
 = 0
j0 = 88,5°
lокн = 1,017
= 0
j0 = 88,5°
lокн = 1,017



