
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложное ндс как суперпозиция чистого и простого сдвигов.
Теоретическое обоснование метода основано на теореме, утверждающей, что любое сложное НДС может быть получено суперпозицией двух простых видов деформирования, например, двух растяжений по главным осям ([[261]], с. 42). Нами принята суперпозиция чистого и простого сдвигов (рис. 2.3.1). С одной стороны, такие условия деформирования характерны для резины между нитями корда, с другой - это удобно для предлагаемой практической реализации в виде дополнительной оснастки к стандартной разрывной машине (см. раздел 2.7).
Схема деформирования при суперпозиции чистого и простого сдвигов приведена на рис. 2.3.1 и 2.3.2. ly = y/y0 - величина деформации чистого сдвига по оси Y; g = tg j - величина простого сдвига вдоль оси X. При сдвиге [5] деформации по главным осям связаны соотношениями: L1 × L2 = 1, L3 = 1. (2.3.1) Главные оси «1» и «2» лежат в плоскости рисунка. Здесь и далее использовано условие несжимаемости резины: L1 × L2 × L2 = 1. (2.3.2)
Простой сдвиг от чистого сдвига отличается способом реализации (рис. 2.3.1), а также тем, что при простом сдвиге, в отличие от чистого, происходит поворот главных осей относительно деформируемого тела. Для определения направлений главных осей деформации введем единичный вектор i, расположенный под углом y к оси Y (рис.2.3.2). В результате деформирования i перейдет в i'. Длина вектора i' зависит от y. Требуется найти значения y и y¢, при которых длина i' имеет максимальное и минимальное значения. Углы Исходные проекции i на оси координат:
В результате деформации чистого сдвига:
Деформация простого сдвига g по оси x, приложенная после чистого сдвига, приводит к соотношениям:
Квадрат длины вектора i ¢ определяется соотношением, следующим из (2.3.5):
Условие экстремума для длины вектора i ¢:
Продифференцировав выражение (2.3.6), получим:
Из (2.3.7) найдем значение угла y, при котором
Направления главных осей определяются углом y¢ (рис. 2.3.2), который связан с углом y соотношением:
Из (2.3.8) можно получить значение для tgy, соответствующее направлениям главных осей:
Подставив (2.3.10) в (2.3.9), получим
Перпендикулярность главных осей следует из соотношений tgy1× tgy2= -1 tgy1¢× tgy2¢= -1, (2.3.12) справедливость которых легко проверяется прямой подстановкой. Удлинения по главным осям L1 и L2 определяются по формуле (2.3.6) подстановкой значений tgy1 и tgy2 из (2.3.10):
Изложим иной способ расчета главных удлинений и главных направлений. Рассмотрим эллипс, в который превращается единичная окружность после наложения деформаций чистого и простого сдвигов (рис. 2.3.2). Его уравнение может быть получено из соотношений, следующих из (2.3.5):
Здесь: x, y – координаты точек единичной окружности до деформирования; X, Y – координаты точек эллипса (центр окружности и центр эллипса находятся в начале координат). Из (2.3.14) получим
Для нахождения главных осей построим характеристическое уравнение (l - корни характеристического уравнения):
Его решение:
Запишем уравнение эллипса в каноническом виде:
Главные удлинения, равные полуосям эллипса a и b, определяются соотношениями [[262]]:
Угол y¢, определяющий направление главных осей, задается соотношением [[263]]
Легко показать, что направления главных осей из (2.3.18) совпадают с (2.3.11). Таким образом, задача построения инвариантов тензора деформации, исходя из величин простого сдвига g и чистого сдвига ly, решена. В Приложении 1 дано решение задачи Вайссенберга с использованием результатов данного раздела.
|
|||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 605; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.156.46 (0.01 с.) |


 и
и  определяют главные направления, которые отличаются на 900, а значения
определяют главные направления, которые отличаются на 900, а значения  и
и  - величины главных удлинений.
- величины главных удлинений.
 . (2.3.3)
. (2.3.3) . (2.3.4)
. (2.3.4)
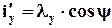 . (2.3.5)
. (2.3.5) . (2.3.6)
. (2.3.6) .
. . (2.3.7)
. (2.3.7) экстремален:
экстремален: . (2.3.8)
. (2.3.8) . (2.3.9)
. (2.3.9)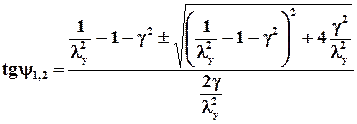 . (2.3.10)
. (2.3.10) . (2.3.11)
. (2.3.11)
 . (2.3.13)
. (2.3.13) (2.3.14)
(2.3.14) (2.3.15)
(2.3.15) .
.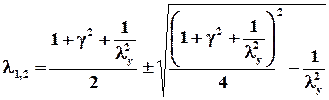 (2.3.16)
(2.3.16)
 ,
, (2.3.17)
(2.3.17) (2.3.18)
(2.3.18)


